1 Introduction
Social tagging provides an easy and intuitive way to annotate, share, and retrieve resources on the Web. In recent years, several studies have focused on constructing tag trees (Almoqhim, Millard, & Shadbolt, 2013; Benz et al., 2010; Candan, Di Caro, & Sapino, 2008; Helic & Strohmaier, 2011; Heymann & Garcia-Molina, 2006; Li et al., 2007; Luo & Chen, 2013; Tsai et al., 2009; Verma et al. 2015). Some of them depended on expert thesauri and tried to derive a model of knowledge domain with precise concepts and relationships. Other studies applied hierarchical clustering algorithms to classify tags based on their similarity. While much work has been centered on the structure of social tagging systems, little is known about the ways of how users navigate such systems.
A tag tree can serve as a navigation tool in many cases, especially when users explore an unfamiliar domain, or their information needs are not specific enough. From the users’ perspective, they may not care whether the semantic relationships are as canonical as those defined by domain experts; yet they would be deeply impressed if the navigation experience with a tag tree is smooth.
In order to adapt to multiple complex domains, some foundational algorithms have been put forward to generate tag trees without expert thesauri (e.g. Benz et al., 2010; Heymann & Garcia-Molina, 2006; Strohmaier et al., 2012b). However, a problem of semantic drift along a path, such as “education->tools->design->blog->business->marketing,” has been noticed (Luo & Chen, 2013). The drift will generate usability issues. On the other hand, the structural balance of the generated hierarchy was not discussed in these studies. Structure usually plays an important role in navigation efficiency. People were found to be consciously or unconsciously weighing the trade-offs between the breadth and depth of the folder hierarchy when organizing their own digital resources (Chen et al., 2012). It is probable that they have similar tastes in navigating a tag hierarchy. Thus structural control is of considerable importance.
The contributions of this study are twofold: (1) an algorithm was developed to construct tag trees with consideration given to both semantic coherence and structural balance; and (2) the effectiveness of a node generality metric, h-degree, was investigated in a tag co-occurrence network. Generality helps to keep the semantic reasonability during the hierarchy development. Proper metrics will benefit the usability of tag trees. Derived from the h-index (Hirsch, 2005), h-degree has been used as a basic indicator for weighted networks (Zhao, Rousseau, & Ye, 2011). Yet it was unknown whether it can be applied to measure node generality of a navigation-oriented tag tree. In this article, it has been verified that h-degree can be applied as a node generality metric since it focuses on the salient meanings of a tag and eliminates the influence of individual co-occurrence of tags.
The paper is organized as follows: Section 1 introduces the background and the contributions of this study. Section 2 reviews the related work. Section 3 discusses the desired features of a tag tree from the perspective of navigation of tagging systems, followed by Section 4, which proposes the algorithm for constructing a desired tag tree from a tagging network. Then Section 5 evaluates the algorithm as well as the node generality metric based on Open Directory Project (ODP) classification. Finally Section 6 is the conclusion as well as suggestions for the future work.
2 Related Work
2.1 Usability of Hierarchies from a User-oriented Perspective
Organizing resources into a hierarchical structure for subject browsing has been recognized as an important tool in information-seeking processes (Golub & Lykke, 2009). A hierarchy can offer searchers information on the collection being searched before any interaction happens. Chen et al. (2012) explored Web resource organization structures based on open-access Web FTP sites. They found that users usually have an upper limit for the depth of the hierarchical structures when organizing resources. With the increasing amount of resources, users preferred to have a flatter structure instead of a deeper one. According to the study, structural complexity needs to be controlled.
Tags are non-hierarchical keywords given by different users to describe information resources. Although unavoidably noisy and ambiguous, these tags reflect the context of the resource domain and the evolution of the knowledge. Thus tags have been widely used in digital resource retrieval, classifications, and summarization. The relationships between tags also facilitate peoples’ understanding of the knowledge of the resource domain. Some studies have tried to generate taxonomies by finding “is-a” or “a-part-of” relationships among concept tags (Si, Liu, & Sun, 2010; Tsui et al., 2010, Verma et al., 2015). Many tags were removed if they were not taken as concepts. Naturally, these taxonomies were not suitable for the purpose of navigation. On the other hand, other studies aimed to develop more loosely structured hierarchies for the purpose of navigating through a large number of resources (e.g. Candan, Di Caro, & Sapino, 2008; Helic et al., 2010; Heymann, & Garcia-Molina, 2006; Huang et al., 2013; Sinclair & Cardew-Hall, 2008). These hierarchies usually involved various tags and were more practical when users were not familiar with the resource domain. This study belongs to this stream and goes further on semantic coherence and structural balance of the hierarchy for the purpose of navigation.
2.2 Methods for Constructing Tag Trees
Two aspects are important in developing a tag tree: selecting quality tags as nodes of the hierarchy and inferring reasonable parent-children relationship among the selected tags.
An empirical study on complex dynamics of tagging systems (Halpin, Robu, & Shepherd, 2007) has shown that consensus around stable tag distributions and shared vocabularies did exist, even if there was no central controlled vocabulary. It is suggested that the popular tags used by different people were valuable in understanding a given domain. Therefore many studies used tag frequency as a simple but effective tag selection criterion (e.g. Strohmaier, Körner, & Kern, 2012; Suchanek, Vojnovic, & Gunawardena, 2008).
The hierarchy generation methods need to detect the hidden relationships among tags and organize them to represent the resource domain. The previous approaches proposed in the literature include three types: (1) developing heuristic rules based on natural language processing (NLP) (Tsui et al., 2010); (2) depending on a thesaurus such as Wordnet (Verma et.al., 2015); and (3) using unsupervised methods (Gemmell et al., 2008; Huang et al., 2013; Heymann, & Garcia-Molina, 2006; Luo, & Chen, 2013; Si, Liu, & Sun, 2010; Zhou et al., 2007). The first two types have limitations in some circumstances because of manual cost or the scope of thesauri.
Among the unsupervised methods, hierarchical clustering-based methods (Begelman, Keller, & Smadja, 2006; Gemmell et al., 2008; Zhou et al., 2007) and tag generality-based methods (Heymann, & Garcia-Molina, 2006; Luo & Chen, 2013) were widely used. Clustering-based methods iteratively partitioned the tags into groups and built the tag tree using either bottom-up or top-down approaches. In contrast generality-based methods first ranked the tags by their generality in a flat tag network and then added a tag as a child of its most similar tag that had already existed in the hierarchy. A typical problem in clustering-based methods is the interpretability of a node’s label. Although related tags were hierarchically clustered, it was difficult to determine which one would represent a category naturally. The generality-based methods were mainly derived from the idea of Heymann and Garcia-Molina (2006), who proposed a simple, efficient algorithm for converting a large set of tags into a navigable tag tree (Camiña, 2010).
According to Heymann and Garcia-Molina (2006), tags were first linked in an undirected graph if their similarity is above a predefined similarity threshold. They were then ranked in descending order by their generality, and these ranked tags were added to the tree through comparing their similarity with the present tags in the tree. Note that, in their study, generality of a node was defined as its centrality in a network, which implied the capability of a node to associate with others. The more nodes a tag associates with, the more generality it has. As a result, these methods tried to arrange the nodes of higher generality close to the root when constructing a tag tree. In Helic et al. (2011) and Strohmaier et al. (2012)’s evaluation, the generality-based methods, DegCen/Cooc and ClosCen/Cos, outperformed the clustering-based ones from semantic and navigational perspectives.
In generality-based methods, tag networks could be built based on tag similarity (Heymann & Garcia-Molina, 2006) and co-occurring frequency (Benz et al., 2010), denoted as Cos and Cooc, respectively; the generality of a tag could be measured by its closeness or degree centrality in the network, represented as ClosCen and DegCen. According to Helic et al. (2011) and Strohmaier et al. (2012), the performance of DegCen/Cooc and ClosCen/Cos had no significant difference. However, the DegCen/Cooc combination has a lower computing cost and therefore is more practical. In this case, this study adopted DegCen/Cooc combination as baseline.
2.3 Issues with Semantic Drift and Structural Skew
Although Heymann’s algorithm and its variations of other studies were considered effective in the above evaluation experiments, there are two issues that have not been solved by either DegCen/Cooc or ClosCen/Cos.
Semantic drift Semantic drift refers to the phenomenon that the semantics of nodes along a path are not coherent; for example, “education->tools->design->blog->business->marketing”. It is strange to reach marketing through design and tools. The semantic drift is obviously detrimental to navigation.
One possible reason for this problem is that the similarity between a child and its parent is not the global optimal value in Heymann’s algorithm. Markines et al. (2009) noticed this issue in their qualitative evaluation. In the study of Tsai et al. (2009), the combination of the proposed sibling independence rule and the hierarchical feature was close to a solution to prevent semantic drift from happening, yet they did not test semantic coherence in their experiment. In our previous study (Luo & Chen, 2013), we have proposed a hybrid method combining clustering and generality, aiming at the semantic coherence inside a sub-tree. However, that work did not consider the representativeness of nodes when deciding siblings for a parent. In the current study, we consider representativeness to keep the diversity among sibling nodes of one parent. This is also a complement to avoid semantic drift.
Structural skew The methods have a risk of structural skew since there is no measure to control the structural balance between branches. When the distribution of tags’ similarity relationships is uneven, this method may result in extremely deep paths and dense branches. According to Wiesman, van den Herik, and Hasman (2004), a hierarchical structure could create usability problems if the breadth and depth of the structure is not well designed. A searcher needs to be able to understand the relationship being presented along the structure to avoid any potential confusion. Song, Qiu, and Farooq (2011) have proposed the idea that the optimal position for a tag in a tree should minimize the change of the current tree in its depth and breadth growth. In Heymann and Garcia-Molina’s approach (2006), if a tag was not similar to an existing tag in the tree above a certain threshold, it would be taken as a child of the root. In some cases, many trivial nodes are set right under the root. Such a structure is harmful to navigation.
3 Rationale for the Proposed Approach
3.1 Desired Features of a Hierarchy for the Purpose of Navigation
The tag tree constructed by the proposed method is supposed to be a user-friendly navigable tool as well as a domain knowledge markup tool. When exploring in a tag tree, users will always track along the paths that most likely lead them to find their desired information. Thus in each decision, they would take the branch whose name most closely meets their search intention. If none of the names indicates a feasible direction, they probably roll back to an ancestor and restart from another branch, or just abandon the exploration.
Based on the above understanding, we define several desired features:
1). The nodes in the tree should be representative. A tag is selected as a node in the tree if, (a) it can represent a group of similar tags in terms of meaning; and (b) it has the capability to associate many other nodes in terms of its role in the network.
According to the selection, all the tree nodes collectively will represent the main content of the resource domain as complete as possible. The meaning of sibling nodes should have the least overlap. The judgement cost for users is thus lowered when they face multiple choices. This idea is borrowed from the field of search engines, where diversified retrieval results are kept to illuminate a searcher’s vague searching intention (Agrawal et al., 2009; Carbonell & Goldstein, 1998; Rafiei, Bharat, & Shukla, 2010). The detailed implementation is shown in Algorithm 1 of Section 4.
2). The relationship between nodes should be reasonable and intuitive. This means that the semantic meaning along a path keeps coherent with as little drift as possible. In addition, the meaning from parent nodes to their children should be increasingly fine-grained.
For arbitrary node ti, i denotes the depth of the node in the tree, and its siblings compose set Bi = {b0i, b1i, … bli,…, bsi}, l∈[0, s]. The path from root to ti is represented as root→t1→t2→…→ti. For example in Figure 1 , the path of a node t3 is root→t1→t2→t3.
To keep semantic coherence, the similarity between the nodes in level j (j ∈[1, i-1]) with ti is:
sim(tj, ti) ≥ sim(blj, ti), where l ∈ [0, s], j ∈ [1, i-1]. (1)
Equation (1) denotes that the similarity between ti and its ancestor tj should be no less than that of the sibling of tj with ti. In Figure 1 , take t3 as an example, the similarity between t3 and t1 is bigger than t3 with each member of B1. So is t3 and t2 with t3 and B2. This criterion ensures semantic coherence not only along a top-down path, but also among the range of children sets to their parents.
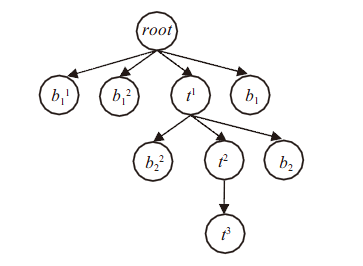
Figure 1. An example of a tag tree. Users track along the paths that most likely lead them to find their desired information by the meaning of nodes. Thus semantic coherence along a path is important for a navigation hierarchy. |
In order to enhance the navigability of the tag tree, representative nodes need to be selected by similarity and generality.
3). The structure is desired to have a relative balance between breadth and depth, as well as a balance of density of each branch.
In an extremely dense or deep hierarchy, users will have to spend considerable time deciding the exploration path. To solve this problem, in this study, the structural balance is controlled by specifying the maximum number of children for each parent by their generality scores. k may vary for different tag datasets, and an empirical value can be estimated in our previous study on the structure patterns of Web resources’ hierarchical organization by the amount of nodes (Chen et al., 2012).
3.2 Measurement of Nodes and Edges in a Tag Network
Given a resource set R, there is a set of associated tags T. The similarity of two tags can be calculated by the cosine of the two vectors. If two tags have been used together in annotating a resource, they probably have a certain association with each other. The higher frequency of their co-occurrence, the stronger their relationship is. If the similarity or co-occurrence frequency of two tags is bigger than the given threshold, there is an edge between them. Thus, the tags form a weighted graph. Heymann and Garcia-Molina (2006) built their tag network by tag similarity, and Benz et al. (2010) by co-occurrence.
In this article, a tag network was built by co-occurrence in order to compare with the well-established solution DegCen/Cooc, according to Helic et al. (2011) and Strohmaier et al. (2012). And the generality of a tag was measured by h-degree.
In a weighted network, the h-degree of a node is defined as h if h is the largest natural number such that the node has at least h links each with strength at least equal to h (Rousseau & Zhao, 2015; Zhao, Rousseau, & Ye, 2011). The h-degree is considered more suitable for weighted networks than indicators based on the underlying unweighted network, for example, degree, since it reflects more information about the links’ strength and structure.
Given a tag t, if at most h of its neighbours co-occur(s) with t at least h times each, the h-degree of t is h. Its neighbours are sorted in descending order by their co-occurrence frequency with t, and then t’s h-degree is identified. The higher h-degree t has, the more popular implication it has.
The difference between h-degree and degree centrality is that the former measures the generality of a node from its salient semantics while the latter just counts all co-occurrence between t and other tags regardless of whether the co-occurrence was caused by individuality. Considering the pervasive individuality in social annotation circumstances, we believed h-degree could better detect salient generality. In the experiment in Section 5.2, we will compare h-degree with degree centrality in their effectiveness in nodes selection.
Representativeness in Feature (1) in Section 3.1 is different from the generality. It is determined by generality and similarity in the proposed method. Nodes of high representativeness will be assigned close to the root. Yet a general node is not necessarily representative if it is very similar to an existing representative node.
4 Algorithm for Constructing Tag Trees
The basic idea of the proposed algorithm is as follows. First, the nodes are divided recursively to at most k smaller groups. Each group is associated with a selected representative node at a particular level by global optimal comparisons. The grouping helps to keep the semantic coherence along a path since the nodes most similar to their representative node are kept in the same sub-tree. The hierarchy is then developed bottom-up by assigning nodes to their most similar representative nodes, the root of a sub-tree. If the generality of a node is larger than the sub-tree root, the node will be discarded to keep the path gradually refined.
4.1 Selecting Representative Tags from T
Selecting the representative nodes involves the judgement of both similarity and generality. Initially, the node of max generality is chosen from a given tag set, and the rest of the nodes are punished according to their similarity to it. The punishment is to keep diversity among siblings and avoid overlapping semantic boundary in each level, as discussed in Feature (1) in Section 3.1.
Algorithm 1. Get representative nodes from tag set L.
In Algorithm 1, L is the initial input tag set; k is a pre-defined maximum number of child nodes under a particular parent; and λ denotes the punishment factor based on similarity. The selected representative nodes will be put into set A as output, which is initially empty.
At first, the input tag set L is assigned to T. The function Ge(t) gets generality for each tag in T and stores them in an array D. The generality refers to the degree centrality or h-degree of a tag in the discussed network. The tag of maximum generality selected in Line 5 is moved from T to the representative node set A in Line 6, and T shrinks gradually. In Line 7 to Line 9, the remaining nodes in T are punished based on their similarity to the selected representative node. In each iteration, at most k representative nodes are selected.
4.2 Constructing Tag Trees
In Algorithm 2, p is the pointer to parent node; L, k, and λ have been introduced in Algorithm 1. The tree is built bottom-up by recursively assigning nodes to its similar representative node.
Algorithm 2. Construct a tag tree.
In each iteration, the representative tags (at most k) are selected from L to A in Line 1. The remaining nodes are divided into groups based on their similarity to nodes in A from Line 7 to Line 9. A sub-tree is built from the nodes of the group, and added to its representative node as its children in Line 11 to Line 15.
If the generality of a node L[i] is bigger than that of the representative node A[i], it will be discarded and will not be taken as a descendant node of A[i], see Line 8. This is to ensure the increasingly fine-grained parent-child relationship, discussed as Feature (2) in Section 3.1. The downside is that some non-representative nodes might be absent from the hierarchical structure. One solution could be first maintaining a list with the discarded nodes, then rerunning the algorithm and organizing them into an additional hierarchy that is then appended to the root as additional branches of the folksonomy.
The tag similarity comparison has been involved in Line 7 of Algorithm 2 and Line 8 in Algorithm 1. Cosine similarity is applied to tag frequency vectors to compare their relationships.
5 Evaluation
5.1 Dataset and Benchmark
The experiment was conducted using dataset PINTS published by Görlitz Olaf. It originally contains 532,924 users, 2,481,698 tags, 17,262,480 resources, and the number of the triples of < user, resource, tag> is 140,126,586. To avoid sparse data space, the dataset was filtered to satisfy the three requirements: tuples containing only English character tags; each tag being used by at least 30 different users; and each resource containing a tag that at least 30 different users have used. These criteria roughly ensure each tag is meaningful and each resource is tagged by at least one well-accepted tag. After the filtering, there are 52,374,650 tuples, including 20,194 tags and 86,465 resources.
Baseline algorithm HTT The baseline algorithm was derived from Heymann and Garcia-Molina (2006), and thus it is denoted as Heymann Tag Tree (HTT). The proposed algorithm in this study is denoted as Navigation-Oriented Tag Tree (NTT). For comparison, we followed the conclusion in Helic et al. (2011) and Strohmaier et al. (2012). In their study, navigability and semantics have been comprehensively evaluated using a series of state-of-arts folksonomy generation approaches, including hierarchical clustering methods and generality-based methods. Finally, the generality-based algorithm with degree centrality for generality and co-occurrence for tag relationships was reported as the best performance, so we implemented the algorithm as our baseline.
However, Helic et al. (2011) and Strohmaier et al. (2012) did not mention the value of a threshold, above which a link was permitted to be a child of an existing tag other than the root. The higher the threshold was, the more trivial nodes were taken as the children of the root. For detail on the function of the threshold, readers may refer to Section B of the origin literature (Heymann & Garcia-Molina, 2006). In this study, the comparison between a child and an existing tag was based on their co-occurrence.
To choose a reasonable threshold in HTT, the trees of HTT were built and compared with the ODP classification with three semantic metrics, i.e. TP, TR, F1 (described in Section 5.2), when the threshold changed from 0 to 10 with step length 1, and from 20 to 100 with step length 10. The results in Table 1 show that the difference is trivial when the threshold varies from 0 to 10 and the performance decreases when the threshold is getting large. Therefore, in the following experiment shown in Figure 2 , the threshold in HTT is set to 0.
Table 1 The semantic evaluation results of different similarity threshold setting values in HTT. |
| Threshold | Degree centrality | h-degree | ||||
|---|---|---|---|---|---|---|
| TP | TR | F1 | TP | TR | F1 | |
| 0 | 0.0448 | 0.0368 | 0.0404 | 0.0509 | 0.0405 | 0.0451 |
| 1 | 0.0448 | 0.0368 | 0.0404 | 0.0509 | 0.0405 | 0.0451 |
| 2 | 0.0448 | 0.0368 | 0.0404 | 0.0509 | 0.0405 | 0.0451 |
| 3 | 0.0448 | 0.0368 | 0.0404 | 0.0510 | 0.0405 | 0.0451 |
| 4 | 0.0448 | 0.0368 | 0.0404 | 0.0510 | 0.0405 | 0.0451 |
| 5 | 0.0448 | 0.0368 | 0.0404 | 0.0509 | 0.0404 | 0.0451 |
| 6 | 0.0448 | 0.0368 | 0.0404 | 0.0509 | 0.0404 | 0.0451 |
| 7 | 0.0447 | 0.0367 | 0.0403 | 0.0509 | 0.0404 | 0.0450 |
| 8 | 0.0446 | 0.0365 | 0.0402 | 0.0508 | 0.0402 | 0.0449 |
| 9 | 0.0445 | 0.0365 | 0.0401 | 0.0507 | 0.0402 | 0.0448 |
| 10 | 0.0443 | 0.0364 | 0.0400 | 0.0506 | 0.0401 | 0.0447 |
| 20 | 0.0417 | 0.0339 | 0.0374 | 0.0479 | 0.0376 | 0.0421 |
| 30 | 0.0382 | 0.0309 | 0.0342 | 0.0446 | 0.0346 | 0.0389 |
| 40 | 0.0344 | 0.0273 | 0.0305 | 0.0406 | 0.0310 | 0.0351 |
| 50 | 0.0316 | 0.0249 | 0.0279 | 0.0378 | 0.0286 | 0.0325 |
| 60 | 0.0298 | 0.0232 | 0.0261 | 0.0360 | 0.0267 | 0.0307 |
| 70 | 0.0279 | 0.0218 | 0.0245 | 0.0343 | 0.0252 | 0.0290 |
| 80 | 0.0264 | 0.0205 | 0.0231 | 0.0328 | 0.0238 | 0.0276 |
| 90 | 0.0252 | 0.0198 | 0.0222 | 0.0319 | 0.0230 | 0.0268 |
| 100 | 0.0241 | 0.0187 | 0.0211 | 0.0308 | 0.0221 | 0.0257 |
5.2 Evaluation of Established Metrics
The biggest challenge in evaluating the navigation of a tag tree is the lack of a baseline. The difficulty is mainly because the resources may come from different domains, and the hierarchies can be generated for different purposes. Researchers compared the auto-generated tag hierarchy against those well-accepted taxonomies in certain resource domains, such as Wordnet, Yago, and Wikitaxonomy. (Strohmaier et al., 2012). In comparing taxonomy generation techniques, Camiña (2010) has proposed several criteria to help develop the evaluation methodology. However, we need to keep in mind that taxonomy serves to represent a logical model of the knowledge domain with precise concepts, instances, and their relationships, rather than facilitating users’ browsing behavior by adapting to a given resource set.
The baseline hierarchy is the Open Directory Project (ODP) classification because it has been used as a well-accepted Web page resource classification since being created. The evaluation metrics are from Strohmaier et al. (2012). The metrics were originally proposed by Dellschaft and Staab (2006). Below is a brief introduction of the metrics. Let AT denotes the automatically generated tag tree, and RT denotes the baseline taxonomy. CAT and CRT are the sets of nodes’ names (i.e. tags) in the tree AT and RT. For each c∈CAT∩CRT, the set ce(c, AT) denotes the names of c’s ancestors and descendants from the root to leaves in tree AT. Similarly, ce(c, RT) refers to their names in RT.
Each c in AT has tp for the precision of the node with regard to RT, and tr for the recall. In addition, TP (Taxonomic Precision), TC (Taxonomic Recall), and F1 (Taxonomic F1) measure the average resemblance between the generated hierarchy and the baseline taxonomy.
Given node c∈CAT ∩ CRT,
(2)
(3)
For the whole tree AT, TP, and TR are based on the contribution of tp and tr from each c.
(4)
(5)
(6)
5.2.1 HTT vs. NTT Algorithms
We calculated the TP, TR, and F1 metrics against the ODP classification for both HTT and NTT. In Figure 2 , the left part is the results using degree centrality for generality, and the right part is those of h-degree. The x-axis denotes punishment parameter λ in the proposed algorithm, and the vertical axis of each line of diagram represents TP, TR, and F1, respectively. The bar in position 0 on the x-axis of each diagram represents the value of HTT algorithm, and the other following positions demonstrate the values of NTT algorithm with different λ values. When λ changes from 0.1 to 1.0, there are 10 groups of bars. In each group, the bars from the left to the right show the effects of structural controlling parameter k, i.e. the TP or TR or F1 when k is assigned as 10, 20, 30, 40, and 50.
Since a tag might be found in multiple ODP branches (e.g. the tag “Sports” appears in both paths “Arts/Movies/Genres/Sports” and “Business/Arts_and_Entertainment/Sports”), the final tp value of a tag is the average of the tp values of all the paths. So is tr.
The TP values of h-degree are higher than those of degree centrality, which means the h-degree is superior to degree centrality as a node generality metric. When the structure parameter k is set from 30 to 50, the results of TP, TR, and F1 are far better than those of when k is 10 or 20. In addition, when λ is 0.4, the TP value of NTT reaches its highest point no matter with degree centrality or h-degree.
Since the F1 value of NTT reaches its maximum when λ = 0.4 and k = 30, the conditions of NTT are set to h-degree with parameters λ = 0.4 and k = 30 by default in this experiment dataset. Under this condition, the TP of NTT is much higher than that of HTT, suggesting a better overlap with the ODP paths, which is likely due to the consideration of the semantic coherence in NTT.
5.2.2 Degree and h-degree Generality Metrics
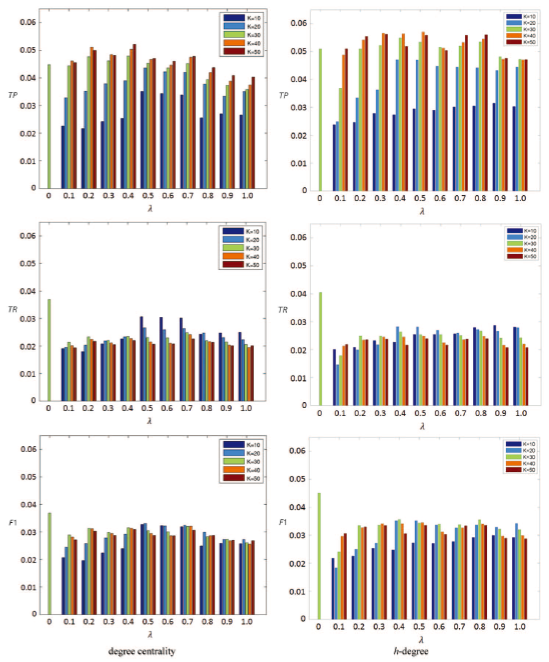
Figure 2. Reference-based evaluation results using NTT algorithm with degree and h-degree. The left part is the results using degree centrality for generality, and the right part is those using h-degree. The x-axis denotes punishment parameter λ and the vertical axis represents the value of TP, TR, and F1, respectively. The bar in position 0 on the x-axis of each diagram represents the value of HTT algorithm, and the other following groups on the x-axis demonstrate the values of NTT algorithm with different punishment parameter λ (λ = 0.1 to 1.0) values. In each group, the bars from the left to the right show the TP/TR /F1 value of structural controlling parameter k (k = 10, 20, 30, 40, and 50). When the conditions of NTT were set to h-degree with parameters λ = 0.4 and k = 30, the TP, TR, and F1 of the proposed algorithm reached the relative best. |
The possible reason why h-degree is superior to degree centrality is that the former concentrates more on semantic meaning than the latter. Although the degree centrality illustrates the width of the node association, it does not indicate the tag’s meaning concentration as the h-degree does. Thus h-degree suits the task of representative nodes selection.
What should be noted for the purpose of navigation is that precision is more important than recall. The reason is that precision reflects both the semantic and structural features of a tag tree, which is essential to the users. Although the TR and F1 were calculated in this experiment, they were not taken as critical criteria of the algorithm performance for the following reasons: (1) the paths in NTT are generally shorter than those in HTT because of the structure control; and (2) some nodes have been removed when building NTT to keep the gradually refined meanings along a path (see Line 8 in Algorithm 2 and its explanation in Section 4.2). Both of the reasons have an effect on TR, and as a result on F1.
Finally, the reason why the values of TP, TR, and F1 are in small scale is mainly that the node names of the experiment dataset are not the same with the category labels in ODP after all. For example, the overlap nodes is 6,053 between the ODP and the NTT tree which was built in default condition of this experiment, i.e. h-degree with parameters λ = 0.4 and k = 30.
5.3 Application Illustration
Two visualized fragments of NTT and HTT are illustrated in Figures 3 and 4. The structure of the HTT tree is not balanced as well as is the NTT tree. For example, at the second level under the root, almost all the tags were considered more similar to the node “software” than “buptsse” by the HTT algorithm. However, in NTT tree, tags were more evenly distributed into different parents to avoid the structural skew.
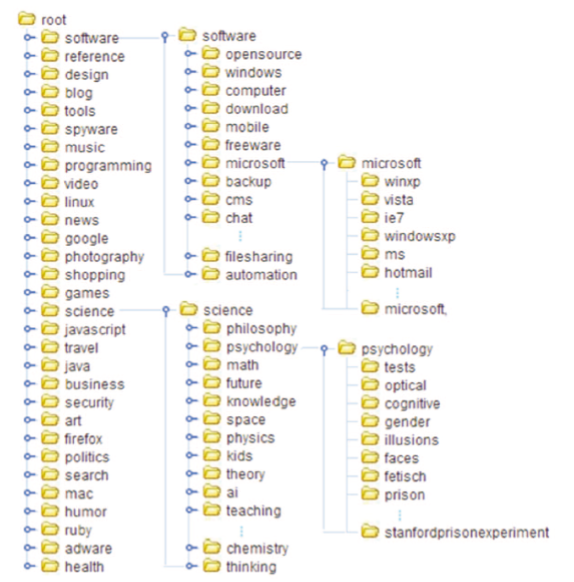
Figure 3. Fragment of NTT tree. |
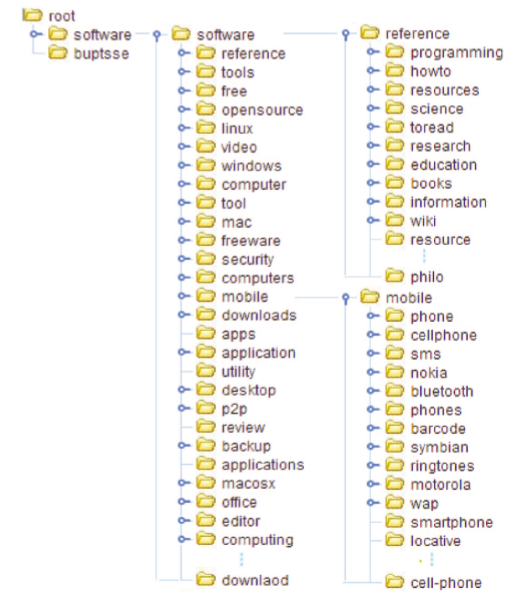
Figure 4. Fragment of HTT tree. |
In addition, the algorithm of HTT is likely to lead to semantic drift. For example, the tags “news,” “games,” and “health” in the HTT tree are located respectively in the path of “/software/tools/web/design/blog/news,” “/software/tools/web/design/cool/fun/games” and “/software/tools/productivity/lifehacks/health.” If users want to look for resources of news, they will never expect to start from “software” to locate these tags. The problem of semantic drift may hurt the navigability of the hierarchy. However, in the NTT hierarchy, the same tags “news,” “games,” and “health” are not under a particular parent according to their representativeness. Instead, they act as heads of a group of branches and are listed directly under the root node, which is easier for users to find.
6 Conclusions and Suggestions for Future Work
This study proposed an algorithm for developing a navigation-oriented tag tree from a tag dataset. The goal of the algorithm is to build a tree characterized by: (1) the ancestors should be more representative than the descendants; (2) the semantic meaning along the node paths needs to be coherent; (3) the children of one parent are collectively exhaustive and mutually exclusive in describing their parent; (4) last but not least, tags are roughly evenly distributed to their upper-level parents to avoid structural skew. The proposed algorithm as well as the h-degree metric has been compared with a well-established solution HTT based on the ODP classification. In the experiments of current study, the NTT with its default condition outperformed HTT. The results suggested a practical, navigation-oriented tag tree, which may facilitate people to hit their targets.
The proposed algorithm will benefit the development of resource navigation systems. It can also be used in managing different online resources, such as academic publications, government documents, and medical communities based on a navigable hierarchy.
What should be highlighted is that the algorithm can be extended to applications in multiple resource domains to generate a flexible domain knowledge structure that is easy to navigate. Easy navigation is possible because the tags mentioned in the algorithm can be not only the social annotations, but also keywords created by authors or experts, as well as automatically extracted from text.
We did a preliminary evaluation in this study. More details are expected on the usability of the hierarchy. As our future work, a thorough investigation into the evaluation methodology is needed, including user studies and comprehensive metrics for navigation performance.
Author Contributions
C. Chen (chenchong@bnu.edu.cn, corresponding author) made the study scheme, guided the literature review and wrote the paper. P.C. Luo (luopc@lib.pku.edu.cn) worked out the algorithm and conducted the experiments. The authors discussed every detail of this article, and elaborated the conclusion together. The work of every author is significant and both of them are first authors.