The reviewing experts who fit the project proposal’s research background are first selected. The most intuitive way of measuring the fitness between an expert and a project proposal is to assume each expert and proposal applicant has a vector of description keywords (related to the research area). The similarity between the two vectors is then selected as the fitness degree. The problem here is that keywords provided by different researchers may have high levels of personal relatedness, or one research point may apply different expressions depending on different researchers’ word choice. We thus make two assumptions about the research descriptions: (1) the topic description is hierarchically structured, in that it has more than one level of detail; and (2) the keywords in the description are (semi-)controlled, so that most of the words can be matched during similarity calculation.

Actually, the assumptions (about the research descriptions) have been met by the NSFC Committee, which set up an Internet-based Science Information System (ISIS) to manage users’ research resumes. A user of ISIS can log in as either an applicant or expert⁽¹⁾(⁽¹⁾Only researchers who have been selected as peer review experts have the role of expert.). With either role, the system will require the users to register their research resumes. Among other variables, the research field section is used to collect scientific research backgrounds, consisting of three fields: familiarity code (FC), research direction(RD), and keywords ( \stackrel{\text{⃗}}{K} ), which correspond to the research area/field, specific research direction, and specific research points (or methods), respectively. Thanks to the NSFC Committee’s efforts to standardize the process, each FC and RD is a pull-down single-selection domain, where RD can only be generated after FC is set. In other words, users with similar research fields and directions will very likely choose the same or a similar familiarity code and research direction. The keywords ( \stackrel{\text{⃗}}{K} ) further consist of five semi-controlled text fields. When double clicked, the system will automatically generate the hottest keywords in the research direction. Users are recommended to employ auto-generated keywords rather than type in their own words, a strategy that greatly increases the probability of users with the same research interests to choose the same keywords to describe their work.

To link with appropriate peer review experts, applicants will usually find or accept recommendations on keywords that best fit their project proposal’s research area. Consequently, we calculate the two parties’ fitness degree hierarchically as follows. If the proposal applicant and the expert have the same familiarity code, they have a fitness score of 0.2. Further, if they have the same research direction, they gain a fitness score of 0.3. Given two keywords vectors, the cosine similarity of the vectors is first calculated, and then scaled with 0.5 as keywords fitness score. The three fitness scores are then added to make the final fitness degree between the applicant and the expert. Considering that the same keywords may have completely different meanings across research fields, the keywords only contribute to the fitness degree if the score of the familiarity code is not 0.

Let RF={FC,RD, \stackrel{\text{⃗}}{K} } be the research field of a researcher R, where each FC and RD is an element of a different set of text descriptions, and \stackrel{\text{⃗}}{K} is a 5-length vector of words. Since a researcher may have two different roles (applicant or expert), A_i and E_i are used to denote the role of applicant and expert of researcher R_i, respectively. Reference to A_i thus means that R_i has submitted a project proposal P_i. Further, given R_i, let \mathrm{R} F_i^a = \{ {FC}_i^a , {\mathit{RD}}_i^a , {\stackrel{\text{⃗}}{K}}_i^a \} be the research field of the applicant’s role, and \mathrm{R} F_i^e = \{ {\mathit{FC}}_i^e , {\mathit{RD}}_i^e , {\stackrel{\text{⃗}}{K}}_i^e \} b the research field of the expert’s role. Based on the notations, fitness degree is defined as follows.

Definition 1 Fitness Degree. Given a proposal P_i and an expert E_j, the fitness degree FD_ij between P_i and E_j can be calculated as Equation (1):

\[FD_{ij}=\left\{\begin{array}{rcl} \Gamma (FC^a_i,FC^e_j)\times (0.2+0.3 \times \Gamma (RD^a_i,RD^e_j)+0.5{∠}(\vec{K}^a_i,\vec{K}^e_j))\ \ if \ i \neq j\\ -1\ \ \ \ \ \ \ else\ \ \end{array}\right.\ \ (1)\]

where ∠(.,.) denotes cosine similarity and Γ(.,.) is a determination equation with Γ(a, b) = 1 if a = b, Γ(a, b) = 0 if a ≠ b. Note here that FD_ij = -1 is more of a flag than a score, as it notifies that an expert cannot review his/her own proposal.

A researcher’s research status is described herein so that when the researcher is appointed as a peer review expert, the confidence level in relation to the value of the expert’s comments can be identified. Because an expert should have enough front-line research experience to grasp the key research points and frontiers of the field and make accurate review comments, we use the H-index and publication timeline to characterize the expert’s status.

Given an expert’s H-index and publication history, the ranking of her/his H-index is first derived based on all experts’ H-indexes from the same research field (i.e. researchers having the same FC^e as the one given). A new parameter ranking percentage can be calculated as dividing the expert’s ranking by the total number of experts in the same research field. This ranking percentage indicates a researcher’s relative academic competence in the research field and can thus convey the meaning of preferable, that is, an expert with a higher H-index may be a preferred candidate for proposal evaluation. Next, the expert’s latest publication year is used to characterize her/his research vitality. The core idea is that a researcher’s ability of following up with academic frontiers declines with the lack of continuous output. The aging model is used to describe this vitality decline. The academic achievement and research vitality score is finally combined into the applicant’s research intensity score as follows.

Definition 2 Research Intensity. Let RP be an expert’s ranking percentage, and PY his/her latest publication year. The research intensity RI of the expert is defined as Equation (2):

where ∆_t = T_c - PY, T_c is the current year, and γ ∈ (0, 1) is the attenuation factor that determines the expert’s declining speed in research intensity along with the number of years without research output. For instance, if γ = 0.95, and a researcher’s H-index ranking is 245/1000, with the latest publication year of 2015, then RP = 245/1000 = 0.245, RI = (1 - 0.245) × 0.95^2017-2015 = 0.681.

Note that in practice, however, an expert’s H-index may not be easy to acquire. This problem can be solved by information provided by the expert’s funding agencies. For example, NSFC is collaborating with ScholarMate⁽²⁾（⁽²⁾ www.scholarmate.com） to allow users to maintain their research resumes online. The data can be used to calculate H-indexes and construct academic social networks (used in the next subsection).

Up to now, fitness degree and research intensity can be used to assign an adequately accurate expert for peer review. It is then necessary to assure impartiality, where there should be little academic association and no conflict of interest between an applicant and the expert.

Academic association is defined based on the network distance between the applicant and expert on academic social networks, which are set up based on various relationships among applicants and experts. Experts having the least degree of association with the applicant can thus be assigned for peer review, where academic association is defined as follows.

Definition 3 Academic Association. Given an applicant A_i and an expert E_j, let H_ij be the number of “hops” in the shortest path between A_i and E_j in the academic social network. The academic association AA_ij between A_i and E_j is then is defined as Equation (3):

where ξ > 1 is the attenuation factor that determines the academic association’s declining speed with respect to the network distance. For instance, let ξ = 2, where the shortest path between an applicant A_i and an expert E_j only has 1-hop (i.e. they have direct relationship), then AA_ij = 2^-1+1 = 1, the highest degree of association two researchers can have. If the shortest path instead has 4-hops, then AA_ij = 2^-4+1 = 0.125, indicating very little association between them.

It is now important to assure that a review expert does not review a proposal in the research area that he/she has also applied for support. Since it is hard to say to what extent the similarity between the expert’s proposal and the reviewing proposal can influence the review result, an alarm value is set so the proposal will not be assigned to this expert if the similarity is larger than the threshold. If this is not the case, the expert is regarded as having no potential/actual conflict of interest with the applicant. Conflict of interest is defined as follows.

Definition 4 Conflict of Interest. Given an applicant A_i and an expert E_j, if E_j submitted P_j, the conflict of interest CoI_ij between A_i and E_j can be calculated as Equation (4):

where τ is a given threshold and \(c_{ij}=\Gamma (FC^a_i,DC^a_j)\times (0.2+0.3 \times \Gamma (RD^a_i,RD^a_j)+0.5{∠}(\vec{K}^a_i,\vec{K}^a_j))\).

Based on Definitions 1 to 4, we can assign the expert that best fits the proposal, has the highest research intensity, least degree of academic association, and no conflict of interest with the applicant for project review. The selectivity degree is used to unify the four concepts as follows.

Definition 5 Selectivity Degree. Given a proposal P_i and an expert E_j, the selectivity degree SD_ij of P_i on E_j is defined in Equation (5).

\[SD_{ij}=\left\{\begin{array}{rcl}-1 \ \ \ if\ \ CoI_{ij}|FD_{ij}|AA_{ij}=-1 \\ \sqrt[3]{CoI_{ij}\times FD_{ij} \times RI_{ij}\times min(\frac{AA^{-1}_{ij}}{\xi ^s})\ }\ \ else \end{array}\right. ,\ \ (5)\]

where | denotes logical OR, min(a,b) is the minimum function that returns the smaller numbers of a and b, and s is a positive integer.

Under Definition 5, if SD_ij = -1, then the proposal will not be assigned to the expert for review due to conflict of interest or avoiding self-reviews. If this is not the case, then the larger the fitness degree and research intensity is, the larger the selectivity degree. A proposal will be more likely assigned to an expert with considerable research intensity, which offers a better fit. As to academic association, for better understanding of ( \frac{{\mathit{AA}}_{\mathit{ij}}^{-1}}{{\xi }^s} , 1 ) , Equation (3) is plugged in and mathematical transformations are made as in Equation (6):

\min \min \left(\frac{{\mathit{AA}}_{\mathit{ij}}^{-1}}{{\xi }^s},1\right) = \min ( \frac{{\xi }^{H_{\mathit{ij}}-1}}{{\xi }^s} , 1 ) =mian ( \frac{{\xi }^{H_{\mathit{ij}}-1-s}}{{\xi }^s} , 1 ) (6)

That is, suppose ξ = 2, and suppose s = 3, then if H_ij = 1 (direct collaboration), we have; if H_ij = 4, we have {\mathit{min}(2}^{H_{\mathit{ij}}-1-s} ,1) = {\mathit{min}(2}^{4-1-3} ,1)= 1; further, if H_ij = 5, we have {\mathit{min}(2}^{H_{\mathit{ij}}-1-s} ,1)= {\mathit{min}(2}^{5-1-3} ,1). From these examples it can be known that selectivity degree will increase with larger H_ij (i.e. smaller academic association). However, when H_ij reaches s+1, the further increase of H_ij will no longer increase selectivity degree. We use s as a hop-lock to avoid the infinite increase of selectivity degree caused by the increase of network distance, and to convey the meaning that all experts with sufficient distance from an applicant will be considered having no academic association with the applicant.

Figure 1 gives an example of expert assignment based on selectivity degree. Figure 1(a) shows an academic social network among six researchers, where applicant A₁ (submitted P₁) has not been selected as the peer review expert, E₂ to E₆ are review experts, andE₂ and E₃ submitted project proposal P₂ and P₃, respectively. Figure 1(a) also gives the research intensity values of all the experts, calculated using the information provided in Figure 1(b) by setting γ = 0.95 (it is assumed here that all the proposal applicants and experts belong to the same research area, i.e. having the same FC). Figure 1(c) gives the fitness degrees among the proposals and experts. If experts are assigned based merely on fitness degree (per the existing works noted above), and if each proposal needs to be reviewed by two experts, then P₁ will be assigned to E₆ and E₃, and P₂ and P₃ will both be assigned to E₄ and E₅. Figure 1(d) (ξ = 2) shows that A₁ is closely related academically to E₆, just as A₂ is related to E₅, and A₃ is related to E₄ and E₅. Compared withA₂ and A₃, E₆ may be more willing to support A₁. Furthermore, it can be seen that E₅ has not directly contributed to research work for five years, so it may not be appropriate for him/her to be a review expert. By also considering the CoIs presented in Figure 1(f) (determined based on the values given in Figure 1(e) for τ = 0.5), the selectivity degrees can be identified as shown in Figure 1 (g). If we use selectivity degree for expert assignment, then P₁ will be assigned to E₃ and E₄, and P₂ and P₃ to E₄ and E₆. It can be seen that the experts with considerable research intensity that have adequate fitness degree with the proposals and relatively less academic association and conflict of interest⁽³⁾（⁽³⁾ Note that if we do not consider CoI, then we will get SD₁₂ = 0.63 > 0.56 = SD14.） with the applicants are selected for peer review.

In practice, a number of proposals need to be reviewed at the same time. Moreover, every proposal needs to be reviewed by more than one expert, and every expert can only receive a limited number of proposals. Hence, given m project proposals and n review experts, let N be the number of review experts a proposal should have, M be the largest number of proposals an expert can receive, and \mathrm{\Omega } ={S {\mathit{SD}}_{\mathit{ij}} | i \in \left[1,m\right] , j \in [ 1 , n ] } be the set of selectivity degrees. Where SD_ij denotes the selectivity degree of proposal P_i on expertE_j, the expert assignment problem is defined as follows.

Definition 6 Expert Assignment Problem. Find a set of 0/1 appointments\(\sum^M_{i=1}\sum^n_{j=1}S_{ij}\times SD_{ij}\)that maximizes and satisfies both Equations (7) and (8):

\[\forall i\in [1,m],\sum^n_{j=1}S_{ij}=N \ \ (7)\] \[\forall j\in [1,n],\sum^m_{i=1} S_{ij}\leq M \ \ (8)\]

Definition 6 defines a version of the 0-1 knapsack problem (Freville, 2004), a famous NP-C problem in computer science. That means that the problem may not be solved in a finite amount of time. Hence, the 0-1 knapsack problem is always handled using dynamic programming, greedy algorithm, and randomized algorithm (Martello & Toth, 1987). In this paper, we adopt the randomized algorithm to solve the problem since it can efficiently find an acceptable solution within a reasonable time period.

Before carrying out the proposed algorithm, an example of possible assignments is given (Figure 2). Based on the selectivity degrees presented in Figure 1(g), Figure 2 presents two possible assignments (where each assignment contains a set of 0/1 appointments), by assuming every proposal should be reviewed by two experts (i.e. N = 2), and each expert can receive no more than two proposals (M = 2). We can then calculate the total selectivity degree to identify the better assignment. The second assignment (Figure 2 (b)) is seen to gain a total selectivity degree of 3.46, much larger than the first assignment (Figure 2(a)), with the total selectivity degree of 2.95.

The possible assignments are seen to increase exponentially with the increase of experts and applicants. It is hard to find the best assignment in a limited amount of time when the number of experts and applicants is large. Hence, we design a randomized algorithm to find an adequately good assignment in a relatively short period of time. The idea is that, proposals to experts are randomly assigned until all the proposals have N review experts, while guaranteeing every expert has fewer than M appointments. The total selectivity degree is then calculated. The process is repeated ROUND (e.g. 10⁵) times, where the assignment with the largest selectivity degree is employed, as noted in Algorithm 1 (Figure 3).

For the generation of fitness degree, we assume applicants and experts are from the same research field, i.e. FD \mathrm{ϵ} \left[ \mathrm{0.2,1} \right] . This assumption is rational since we need experts with similar research content for reviewing, where the assumption can be easily confirmed by matching the familiarity codes of experts and applicants before assignment. We further assign the fitness degree subjects to the Normal Distribution N(0.6, 0.2) so that the average fitness degree will be 0.6, where 95% of the fitness degree will fall into [0.2, 1]. This assumption is based on the intuition that the researchers in the same research area/field will have roughly similar research content, where the probability of having exactly the same research content or extremely different content will be small. During the generation, values lower than 0.2 are assigned to the value of 0.2, and values greater than 1 are assigned to 1.

As to research intensity, we assume a uniform distribution of U(0,1) for generation. According to Definition 2, the ranking percentage part (i.e. 1-RP) is subject to uniform distribution. And if we assume all the researchers’ publication years are also subject to uniform distribution, the attenuation factor part ( {\gamma }^{∆t} ) will not affect the distribution of research intensity as a whole.

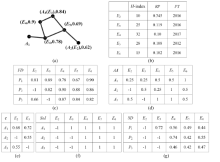
For academic association, we generate network distances based on the Sixth Degree Segmentation Theory (or Small World Phenomenon). Small World Phenomenon proposes that in a social network, there will be no more than six hops before a person can reach any stranger in the network (Milgram, 1967). This phenomenon is also closely applied to academic social networks, due to the particularity of academic circles (e.g. 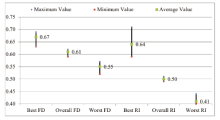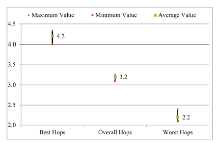which consist of people with similar research backgrounds who are very willing to know each other) (Cainelli et al., 2015). Hence, we assume a researcher in the academic social network can reach 70% of other researchers in less than three hops, and can reach anyone in the network in less than six hops. 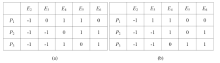More specifically, we assign the probability of reaching h-hop as 0.1, 0.2, 0.4, 0.1, 0.1, 0.1 for h = 1, 2, ..., 6, respectively. Finally, for conflict of interest, we randomly generate a matrix that contains 10% of -1s and 90% of 1s.

During the simulation, the algorithm parameters are set as: m = 200, n = 500, N = 4, M = 8, ROUND = 10⁸. Note that 200 is a sufficiently large number of applicants in practice. Since according to statistics, the total number of proposals is subject to management science, where NSFC 2016 is 8,293 and there are 57 familiarity codes in management science. So there is an average of 145 proposals per familiarity code. Also note that while the proposed algorithm is expected to find a better result with a larger ROUND, our experimental results show that ROUND = 10⁸ can return a good assignment for m = 200⁽⁴⁾（⁽⁴⁾ A larger m may need a larger ROUND due to the increase of solution space (search space).）.

Since the output of the randomized algorithm is non-deterministic, we run the algorithm 100 times (see Figures 4 and 5 for analysis). For each run, we record the average fitness degree, research intensity, and academic association of the best assignment (best value) of all the ROUND assignments (overall value) and of the worst assignment (worst value). We then calculate the averages within the best, overall, and worst values of the 100 runs.

Figure 4 plots the maximum, average, and minimum values of best, overall, and worst FD/RI (of the 100 runs), where it is found that (1) after large amounts of sampling, the average values of the overall FD and RI converge to their corresponding theoretical value, and these values are the expected values when the experts are randomly assigned for peer review; (2) the maximum, average, and minimum values of the best FD and RI are significantly larger than their corresponding overall and worst values; (3) the average fitness degree among the experts and applicants of the best assignment is approximately 10% higher than the overall assignments, and 22% higher than the worst assignment; and (4) the average research intensity of the experts of the best assignment is approximately 28% higher than the overall assignments, and 56% higher than the worst assignment. That is, the proposed algorithm can always find experts with considerable research intensity having a better fit with proposal applicants.

For academic association, we plot the maximum, average, and minimum hops of the best, overall, and worst assignments (see Figure 5). The results are very similar to those of fitness degree and research intensity. The converged (i.e. expected) average hops (between an expert and the applicant) is 3.2. Compared to the overall assignments and the worst assignment, on average our algorithm can find the experts for peer review with one or two hops away from the applicants.

The time overhead of the algorithm is analyzed to verify whether it is feasible for expert assignment in practice. The same set of parameters is used here as those used in Section 3.1, except that m is varied from 10, 20, 50, 100, and 200 to 500 for verification. This approach is used because according to Algorithm 1, besides ROUND, the algorithm’s efficiency is mainly determined by m. Correspondingly, the algorithm needs approximately 50, 100, 250, 500, 1,000, and 2,500 seconds to return the best assignment. The results show that: (1) when ROUND is fixed, the algorithm’s time overhead is linearly correlated with the input m; (2) an assignment of 200 proposals needs less than 17 minutes on a computer with Intel Core i7-6700 (3.4GHz) and 8G memory, which is adequately efficient for the non-real-time expert assignment problem in this paper; (3) when there are large numbers of proposals that need to be assigned, a p-node parallel computing network can easily increase the speed of p times (e.g. the assignment of 200 proposals will need less than one minute if p = 20), and the parallelization can be very easily deployed. In this case each round of assignments can be executed independently, and the results of each round can be efficiently integrated and compared in one run.

M.L. Yue (yueml@whlib.ac.cn) proposed the research question, designed the methods, and designed and implemented the algorithm. K.L. Tian (23950839@qq.com) wrote the manuscript. T.C. Ma (atc@whlib.ac.cn, corresponding author) designed the method and revised the manuscript.