1 Introduction
Universities, as centres for higher education and research, have long vied quietly and nearly invisibly for the top positions on the international arena. The grounds on which universities compete to attract students and raise funds for their scientific activities include reputation, prizes awarded to professors and students, and contributions to significant discoveries. The first world ranking of universities was formulated by what was then Shanghai Jiao Tong University’s Institute of Higher Education (now the Graduate School of Education) (Cheng & Liu, 2007; Liu & Cheng, 2005; Liu, Cheng, & Liu, 2005). It was soon followed by others such as the Times Higher Education Supplement’s QS World University Ranking (Times QS ranking) (Buela-Casal et al., 2007) and the Leiden ranking in 2007 (Waltman et al., 2012), which measures the results of world universities’ scientific and teaching performance. These rankings gave rise to another much more complex scenario in which universities shifted from local competition, i.e. among institutions in the same country/region, to compete globally, with comparisons crossing national borders (Azman & Kutty, 2016; Kauppi, 2018; Marginson, 2007; Musselin, 2018; Ordorika & Lloyd, 2015). Higher education institutions were therefore driven to update their objectives to adapt to the new situation, which included improving their positions on rankings in a bid for prestige as research bodies (Lim & Øerber, 2017; Millot, 2015; Zhang, Bao, & Sun, 2016). Such competition was heightened by governments’ need to enhance access to higher education and strengthen their countries/regions’ presence on the list of the most highly reputed universities (Bornman, Mutz, & Daniel, 2013; Guironnet & Peypoch, 2018; Musselin, 2018). Some governments have implemented different types of initiatives to support the internationalisation of their higher education institutions.
Each ranking is generated in keeping with a specific methodology, using bibliometric and other types of indicators. A given institution’s position may vary depending on the methodology used. In the Shanghai Jiao Tong University (ARWU) and Leiden rankings, classification prioritises research, whereas the Times Higher Education (THE) list stresses reputation, measured on the grounds of questionnaires sent out to reputed academics in different areas (Ordorika & Lloyd, 2015; Shin & Toutkoushian, 2011).
According to Safón (2013), the most influential global rankings are ARWU, THE and QS, whose methodological differences have prompted studies aiming to identify the strengths and weaknesses of each. ARWU, based primarily on research and academic performance, consists of six indicators, including the award of prestigious distinctions such as the Nobel Prize to students or faculty. Safón (2013) contends that this indicator favours older institutions in countries/regions with long ranking traditions. THE in turn, uses now 13 performance indicators one of them related to academic prestige, assessed on the grounds of large-scale surveys. It had been criticised for its regional bias, now it take care to get a better sample of academics from over the world.
Several authors have analysed and compared the methodologies used by ranking institutions (Buela-Casal et al., 2007; Van Raan, 2005). Marginson (2007) compared the scientific activity of Australian universities listed on the ARWU and THE rankings, identifying bias in the methods used by both and hence in their results. He deemed that combining subjective reputational data with objective research data, as in the THE, was not a valid approach, and also detected a strong tendency in the ARWU methodology to favour universities in English-speaking countries/regions. Aguillo et al. (2010) compared five well-known rankings, ARWU, THE, Leiden, WR (Web Ranking of World Universities (for 2005-2008)1)(1http://www.webometrics.info/) and HEEACT (since 2012 executed and released by National Taiwan University (NTU)).2(2http://nturanking.lis.ntu.edu.tw/about/introduction) The three measures used, developed by Bar-Ilan, Levene, and Lin (2007), included the size of the overlap, Spearman’s footrule and the M measure. They found the ARWU ranking to be the one most strongly based on bibliometric data. However, other authors find serious problems to use this ranking for evaluation purposes (van Raan, 2005) or they think that the criteria used are not relevant for academic institutions (Billaut, Bouyssou, & Vincke, 2010). Dobrota et al. (2016) propose an alternative approach to the QS score they called Composite I-distance Indicator (CIDI), which could be applicable to other global rankings.
In their statistical analysis of known rankings, Bornmann, Mutz, and Daniel (2013) explored one of the main bibliometric indicators used by the Leiden ranking, namely the proportion of papers published by a university that lies within the 10% most cited (PPtop10%). These same authors pointed out that a more sophisticated statistical model than deployed by the editors of the Leiden ranking3(3http://leidenranking.com/leidenranking.zip) could be an alternative to the stability intervals used by that ranking described by Waltman et al. (2012).
Taking the variable PPtop10% as a basis, Bornmann, Mutz, and Daniel (2013) analysed several significant questions in connection with the Leiden ranking, the first being the accuracy of the positions and stability intervals predicted by the multi-level regression model proposed. Another question posed related to whether differences in the impact factor explained scientific research rankings and whether a relationship could be found between such differences and the country/region where the university is located (Bornmann & Moya-Anegón, 2011). A final issue addressed by these authors was whether inter-university differences could be explained by economic factors (Per Capita Gross Domestic Product (GDP PC), Gross Domestic Product (GDP), a country/region’s total area and population) or by the number of papers published by a given university.
Marginson (2007) used statistical methodology to compare each country/region’s economic status, calculated as GDP and GDP per capita, to the number of its universities in the ARWU top 100 and top 500. In another paper, Marginson and van der Wende (2007) compared each nation’s share of world economic capacity against the proportion of research universities in the ARWU top 100 and top 500.
Docampo (2008) analysed the impact of the ARWU since its first edition and reviewed the criticism and updates of its methodology for listing universities. The author also aggregated the data for each country/region’s universities and weighted the size of national economies measured as the share of each one’s gross domestic product (GDP) in the world total in 2006.
Other authors, including Kempkes and Pohl (2010) and Johnes and Yu (2008) analysed German and Chinese universities’ activity on the grounds of R&D input and output, using data envelopment analysis (DEA) to determine their efficiency and total productivity. Rhaiem (2017), makes a systematic review about research efficiency. Using several electronic databases, the author brings a set of inputs and outputs related to this issue. In the same way, Barra et al. (2018), measures the efficiency of Italian higher education using parametric (Stochastic Frontier Approach) and non-parametric (DEA) methodology.
The primary aim of the present study is to analyse the relationship between a number of socio-economic indicators for selected countries/regions and performance measured as the number of their universities positioned in the ARWU top 100 and top 500. Multiple regression techniques were used for this analysis. A second objective was to identify how the indicators analysed would have to change for a country/region to raise the number of its universities listed and their position on the ARWU. The reasons for choosing ARWU rankings were similar to the explanations provided by Marginson (2007), Docampo (2011, 2012, 2013), and Ordorika and Lloyd (2015), i.e. because they “are credible, based on solid, transparent numerical data…”, and “because it is the only global ranking that focuses on research activities of the universities…”. The properties, strengths, weaknesses and reliability of the ARWU scale were also studied by Docampo (2008, 2011). This author contended that the emphasis on international publications and citations (per year and cumulative) may bias the ranking, favouring the English language and traditional institutions. Docampo also noted, however, that aggregating data for the sciences by country/region smooths the effects of these indicators. The use of indicators that take the distinctions awarded to university teachers and students into consideration has been addressed by a number of authors, including Docampo (2008) and Bornmann, Mutz, and Daniel (2013). Their argument is that history may weigh significantly on the results, enabling institutions to rank in the upper echelon on the grounds of just a few shining moments.
The present study differs from the ones referenced above in the multivariate approach adopted, which proposes multiple linear regression models and transformations of the predictor and response variables.
2 Materials and methods
This section contains a detailed description of the data retrieved and the methods used for the analysis and the model proposed.
2.1 Data and variables
In this study the data contained in the Shanghai Jiao Tong University (Liu, Cheng, & Liu, 2005) for 2012, retrieved from the ARWU website4(4http://www.shanghairanking.com/ARWU2012.html) were aggregated by country/region. Jiao Tong data collection depends neither on the institutions assessed nor on subjective data such as opinion surveys among peers to determine an institution’s prestige (Docampo, 2008). Rather, the ARWU classification uses six indicators to rank institutions: alumni: institutions’ former students who win Nobel Prizes or Fields Medals; award: institutions’ staff who win Nobel Prizes or Fields Medals; HiCi: highly cited researchers in 21 broad subject categories; N&S: papers published in Nature and Science over the last five years; PUB: number of articles indexed in the Science Citation Index—Expanded and Social Sciences Citation Index; and PCP: per capita performance with respect to the size of an institution measured in terms of its full-time equivalent academic staff (Docampo, 2008; Liu, Cheng, & Liu, 2005). The present study analyzes the number of each country/region’s universities listed on the ARWU 2012 top 100 and top 500, taking Chinese Hong Kong, Chinese Taiwan, and Chinese mainland as separate entities. In contrast to the study conducted by Bornmann, Mutz, and Daniel (2013), no country/region groupings were assumed, i.e. each country/region’s behaviour was implicitly assumed to be independent. Moreover, the ranking’s limitation to 100 or 500 universities was assumed to have no impact on the dependent variable (see Liang & Zeger, 1993): the number of each country/region’s listed universities, treated as a continuous variable in light of its wide range of variation. The logarithm of the number of ranked universities was used in lieu of the actual number to prevent the model from yielding negative values for this variable.
The choice of indicators was influenced by related articles. Bornmann, Mutz, and Daniel (2013) assessed the Leiden ranking with a multilevel statistical method in which the country/region level was partially defined on the grounds of purchasing power parity GDP per capita (PPP GDP PC) and population size. Docampo (2008) measured country/region size in terms of its share of world GDP. Bornmann, Mutz, and Daniel (2013) assumed that countries/regions with a higher PPP GDP PC would make more funding available for science and therefore would be expected to conduct higher level research. They also assumed that countries/regions with a larger population would be more likely to have a larger pool of potential scientists.
Finally, bearing in mind that two countries/regions with the same level of per capita GDP may differ in terms of human development, in the present study country/region level was measured not only on the basis of economic development, but also on the Human Development Index (HDI), in which people and their capabilities are the ultimate criterion for assessing a nation/region’s global level.
Four indicators were reviewed: population size, gross domestic product (GDP), gross domestic product per capita (GDP PC) and the HDI, all for 2012. The aim was to statistically analyse the effect of socio-economic indicators on the aggregate number of universities per country/region in the ARWU 2012 ranking.
HDI is a composite indicator, comprising three main dimensions or components: health, education and standard of living. Equal opportunities and development are social objectives pursued by nations the world over. The United Nations Development Program (UNDP) calculates its HDI yearly on the grounds of life expectancy at birth, years of schooling and GDP PC. The most recent version, known as the inequality-adjusted HDI, also takes the degree of inequality into consideration. In a society with total equality (according to this measure), the HDI and equality-adjusted HDI values would concur. Despite the criticism levelled against this indicator, it merits attention, as it has been constantly revised and improved. Moreover, UN reports are informative and contain reliable and comparable international data.
Further to the approach set out in Bornmann, Mutz, and Daniel (2013), GDP PC was included in the calculations because countries/regions with greater economic resources may be assumed to have more funds to incentivize research and hence high level research.
GDP and GDP PC data were retrieved from the World Bank website5(5http://data.worldbank.org/data-catalog/GDP-ranking-table?) and the Human Development Index from United Nations website6(6https://data.undp.org/dataset/Table-1-Human-Development-Index-and-its-components/wxub-qc5k) for 21 March 2014. Since these tables contained no data on GDP or GDP per capita for Chinese Taiwan, the respective values were retrieved from the Chinese Taiwan Statistics Bureau website7,8,9(7http://eng.stat.gov.tw/public/data/dgbas03/bs2/yearbook_eng/y008.pdf8http://eng.stat.gov.tw/public/data/dgbas03/bs2/yearbook_eng/y093.pdf9http://eng.stat.gov.tw/ct.asp?xItem=25280&ctNode=6032&mp=5) on 21 March 2014.
2.2 Statistical procedures
The data for the 500 universities listed on the ARWU 2012 were aggregated by country/region. The data for Chinese mainland, Chinese Hong Kong, and Chinese Taiwan were considered separately. The criterion for including a country/region in the analysis was its presence in the ranking from 2008 to 2012 with at least one university. This eliminated all but 39 nations. Table 1 gives the values for the 39 countries/regions with at least one institution in the top 500, along with their respective economic size measured as GDP, population, HDI, and GDP PC. The table also lists the number of each country/region’s universities in the top 100, each country/region’s share of world GDP and the country/region share on the top 500 ARWU universities.
Table 1 Values of indicators studied (2012). |
| Country/region | GDP per capita | HDI 2012 | GDP Mill ($) | Population 2012 | N.U. (500) | 500% | Median_ NU | Global share of GDP | N.U. (100) |
|---|---|---|---|---|---|---|---|---|---|
| United States (USA) | 51,748.6 | 0.94 | 16,244,600 | 313,914,040 | 150 | 30.00 | 153.20 | 22.64 | 53 |
| United Kingdom (GBR) | 39,093.5 | 0.88 | 2,471,784 | 63,227,526 | 38 | 7.60 | 39.00 | 3.44 | 9 |
| Germany (DEU) | 41,862.7 | 0.92 | 3,428,131 | 81,889,839 | 37 | 7.40 | 39.00 | 4.78 | 4 |
| Chinese mainland* (CHN) | 6,091.0 | 0.70 | 8,227,103 | 1,350,695,000 | 28 | 5.60 | 21.80 | 11.47 | 0 |
| Canada (CAN) | 52,219.0 | 0.91 | 1,821,424 | 34,880,491 | 22 | 4.40 | 22.00 | 2.54 | 4 |
| Japan (JPN) | 46,720.4 | 0.91 | 5,959,718 | 127,561,489 | 21 | 4.20 | 26.20 | 8.31 | 4 |
| France (FRA) | 39,771.8 | 0.89 | 2,612,878 | 65,696,689 | 20 | 4.00 | 21.80 | 3.64 | 3 |
| Italy (ITA) | 33,071.8 | 0.88 | 2,014,670 | 60,917,978 | 20 | 4.00 | 21.40 | 2.81 | 0 |
| Australia (AUS) | 67,555.8 | 0.94 | 1,532,408 | 22,683,600 | 19 | 3.80 | 17.40 | 2.14 | 5 |
| Netherlands (NLD) | 45,954.7 | 0.92 | 770,555 | 16,767,705 | 13 | 2.60 | 12.40 | 1.07 | 2 |
| Spain (ESP) | 28,624.5 | 0.89 | 1,322,965 | 46,217,961 | 11 | 2.20 | 10.40 | 1.84 | 0 |
| Sweden (SWE) | 55,041.2 | 0.92 | 523,806 | 9,516,617 | 11 | 2.20 | 11.00 | 0.73 | 3 |
| Korea (KOR) | 22,590.2 | 0.91 | 1,129,598 | 50,004,441 | 10 | 2.00 | 9.60 | 1.57 | 0 |
| Chinese Taiwan (TWN) | 20,335.9 | 0.91 | 4,741,490 | 23,315,822 | 9 | 1.80 | 7.40 | 1.00 | 0 |
| Austria (AUT) | 46,642.3 | 0.90 | 394,708 | 8,462,446 | 7 | 1.40 | 7.00 | 0.55 | 0 |
| Belgium (BEL) | 43,372.4 | 0.90 | 483,262 | 11,142,157 | 7 | 1.40 | 7.00 | 0.67 | 1 |
| Switzerland (CHE) | 78,924.7 | 0.91 | 631,173 | 7,997,152 | 7 | 1.40 | 7.40 | 0.88 | 4 |
| Brazil (BRA) | 11,339.5 | 0.73 | 2,252,664 | 198,656,019 | 6 | 1.20 | 6.20 | 3.14 | 0 |
| Israel (ISR) | 30,413.3 | 0.90 | 240,505 | 7,907,900 | 6 | 1.20 | 6.60 | 0.36 | 3 |
| Finland (FIN) | 45,720.8 | 0.89 | 247,546 | 5,414,293 | 5 | 1.00 | 5.40 | 0.34 | 1 |
| Chinese Hong Kong (HKG) | 36,795.8 | 0.91 | 263,259 | 7,154,600 | 5 | 1.00 | 5.00 | 0.37 | 0 |
| New Zealand (NZL) | 37,749.4 | 0.92 | 167,347 | 4,433,100 | 5 | 1.00 | 5.00 | 0.23 | 0 |
| Denmark (DNK) | 56,325.7 | 0.90 | 314,887 | 5,590,478 | 4 | 0.80 | 4.00 | 0.44 | 2 |
| Norway (NOR) | 99,557.7 | 0.96 | 499,667 | 5,018,869 | 4 | 0.80 | 4.00 | 0.70 | 1 |
| Ireland (IRL) | 45,931.7 | 0.92 | 210,771 | 4,588,798 | 3 | 0.60 | 3.00 | 0.29 | 0 |
| Portugal (PRT) | 20,165.3 | 0.82 | 212,274 | 10,526,703 | 3 | 0.60 | 2.20 | 0.30 | 0 |
| South Africa (ZAF) | 7,507.7 | 0.63 | 384,313 | 51,189,306 | 3 | 0.60 | 3.00 | 0.54 | 0 |
| Chile (CHL) | 15,452.2 | 0.82 | 269,869 | 17,464,814 | 2 | 0.40 | 2.00 | 0.38 | 0 |
| Greece (GRC) | 22,082.9 | 0.86 | 249,099 | 11,280,167 | 2 | 0.40 | 2.00 | 0.35 | 0 |
| Hungary (HUN) | 12,530.5 | 0.83 | 124,600 | 9,943,755 | 2 | 0.40 | 2.00 | 0.17 | 0 |
| Poland (POL) | 12,707.9 | 0.82 | 489,795 | 38,542,737 | 2 | 0.40 | 2.00 | 0.68 | 0 |
| Russia (RUS) | 14,037.0 | 0.79 | 2,014,775 | 143,533,000 | 2 | 0.40 | 2.00 | 2.81 | 1 |
| Singapore (SGP) | 51,709.5 | 0.90 | 274,701 | 5,312,400 | 2 | 0.40 | 2.00 | 0.38 | 0 |
| Argentina (ARG) | 11,573.1 | 0.81 | 475,502 | 41,086,927 | 1 | 0.20 | 1.00 | 0.66 | 0 |
| Czech Republic (CZE) | 18,682.8 | 0.87 | 196,446 | 10,514,810 | 1 | 0.20 | 1.00 | 0.27 | 0 |
| India (IND) | 1,489.2 | 0.55 | 1,841,710 | 1,236,686,732 | 1 | 0.20 | 1.60 | 2.57 | 0 |
| Mexico (MEX) | 9,748.9 | 0.78 | 1,178,126 | 120,847,477 | 1 | 0.20 | 1.00 | 1.64 | 0 |
| Slovenia (SVN) | 22,000.1 | 0.89 | 45,279 | 2,058,152 | 1 | 0.20 | 1.00 | 0.06 | 0 |
| Turkey (TUR) | 10,666.1 | 0.72 | 789,257 | 73,997,128 | 1 | 0.20 | 1.00 | 1.10 | 0 |
2.3 Outliers detection
The first step in the statistical analysis consisted of obtaining the values for the indicators selected to reveal the possible existence of outliers or correlations (Rousseeuw, P. J. & Leroy, A. M., 2003; Verardi, V. & Croux, C., 2009). Four outliers (countries/regions) were identified for population (Brazil, United States, India, and Chinese mainland) and three for GDP (Japan, Chinese mainland, and United States). Norway’s GDP per capita was found to be an outlier on the high end, while the HDIs for South Africa and India were outliers on the low end. With the exception of HDI, all the variables studied were transformed into logarithmic monotonic functions in order to simplify the calculations without affecting the information contained increasing at the same time, the power and characteristics of distribution. Significant correlations were subsequently identified between the two general indicators (population and GDP) ρ=0.799 with p-value 0.000 and between the two socio-economic indicators (GDP PC and HDI) ρ=0.918 with p-value 0.000. The Bartlett sphericity test (Peña, 2002) showed that the hypothesis whereby the inter-indicator correlations were not equal to zero was highly significant (p<0.01).
2.4 Principal Component Regression
The findings above were an indication that the direct application of a classical multiple linear regression model (MLR) based on ordinary least squares (OLS) was not a good modelling option, for the presence of multi-colinearity would clash with the assumption of independence among the explanatory variables. Certain assumptions must be made in the MLR model, such as the normality of the observed variable as well as of the standard errors and residuals for the assumptions and theoretical background, see Kutner, Nachtsheim, Neter, and (Li, 2005). In the presence of multi-colinearity, the inverse of the correlation matrix is singular or nearly singular; as a result, the estimates obtained with OLS directly would not be reliable. One alternative for surmounting this difficulty is to use biased regression models such as principal component regression, which was the solution adopted in the present study. The next step in developing the model is to verify whether multiple regression using the explanatory variables obtained with principal components is the method best suited to the data retrieved.
Principal components is a multivariate technique for reducing the size of the data matrix. As established in the Kaiser-Gutman rule (Kaiser, 1991), eigenvalues greater than or equal to 1 on the eigenvector (λ1, λ2,…λk) are selected, for values close to zero constitute components that explain very little of the variability in the original data matrix.
The primary characteristic of the component scores so obtained, used as explanatory variables, is that they are not correlated. The dependent variable used in this case was the aggregate indicator “number of a country/region’s ranked universities”.
2.5 The log transformation
We decided to adopt a common practice in regression contexts which is to apply a log transformation to the variables because it helps meeting the required assumptions of the inferential statistics used in the regression, for example making distributions less skewed more close to normality. Moreover, it is also used to make patterns in the data more interpretable and data scales more comparable.
Monotonic (natural log) transformation was applied to favour positivity of the estimated value of the variable studied. Y was defined as the indicator “a country/region’s number of ranked universities”, whereby Y ≥ 0, and since the set studied satisfied the inequality strictly, log(Y) ≥ 0. The round function (Exp (log(Y)) was used for the final estimation.
2.6 Robust Regression
The results obtained with MLR may be distorted by the presence of the existence of outliers. Two types of statistical techniques are suitable for such situations. The first is univariate and multivariate detection and ultimately the elimination of outliers in a second application of MLR methodology. The second is the use of robust MLR methods that are unaltered by the presence of outliers. Both techniques were used here to guarantee a better understanding of the effect of socio-economic explanatory variables on the response variable “classification in the ARWU”.
The three best known methods for robust regression are the M- (maximum likelihood), R- (range regression) and L- (linear combination of order statistics) estimators. The M-estimator was chosen for the present study. The most popular weighting functions are the Huber and the Tukey estimators.
Outliers were detected in this method using Cook’s distance, which is a measure that combines the extreme values of the predictor variables (leverage) and high residual values.
In a second round of statistical processing of the aggregated data, some of the indicators were separated into mutually exclusive sub-sets on the grounds of a key characteristic that distinguished between the elements in the various sub-sets. Dummy variables (also known in the statistical literature as indicator variables), defined as variables whose value is 1 if the criterion studied is satisfied and 0 otherwise, were used to represent the sub-sets.
The relationship among sub-sets for different indicators was analysed with the chi-square test, developed to accept or reject the existence of independence among groups of indicators by comparing the empirical data to the theoretical findings calculated assuming its existence.
R (version 3.02), SPSS (version 20) and Minitab 16 were the software used for principal components and other statistical analyses.
3 Results
Data were aggregated for the 45 countries/regions with at least one university on the list of the ARWU 2012 top 500. Nonetheless, Table 1 gives only the 39 countries/regions that met the first condition (the total number of universities for the countries/regions selected was 492). The top 100 universities were located in 16 countries/regions, in which the United States clearly prevailed, with 53 of the top 100 and 150 of the top 500 universities, followed by the United Kingdom with 9 in the top 100 and 38 in the top 500.
The search of statistical relationships between related variables via linear regression analysis may be distorted by the presence of spurious correlations between regressors and the predicted variable. This effect may be more dramatic for analysis of cross-sectional nature as in the present case. To discard these suspects in our analysis we have searched correlations and partial correlations. As Table 2 shows, the correlation values obtained at the 10% significance level guaranteed the relevance of the regression analysis performed; consequently, a linear statistical relationship could be concluded to exist between the predicted variable and the proposed regressors.
Table 2 Correlations and partial correlations |
| CORRELATIONS AND P-VALUES | ||||
|---|---|---|---|---|
| HDI | GDP PC | GDP | POP | |
| NU | 0,434 | 0,488 | 0,685 | 0,290 |
| (0,006) | (0,002) | (0,000) | (0,074) | |
| IDH | 0,918 | -0,122 | -0,599 | |
| (0,000) | (0,459) | (0,000) | ||
| GDP PC | -0,051 | -0,586 | ||
| (0,760) | (0,000) | |||
| GDP | 0,839 | |||
| (0,000) | ||||
| PARTIAL CORRELATIONS AND P-VALUES Control Variable (IDH) | ||||
| GDP_PC | GDP | POP | ||
| NU | 0,251 | 0,825 | 0,762 | |
| (0,128) | (0,000) | (0,000) | ||
| Control Variable (GDP_PC) | ||||
| IDH | GDP | POP | ||
| NU | -0,041 | 0,814 | 0,814 | |
| (0,805) | (0,000) | (0,000) | ||
| Control Variable (GDP) | ||||
| IDH | GDP_PC | POP | ||
| NU | 0,716 | 0,718 | -0,719 | |
| (0,000) | (0,000) | (0,000) | ||
| Control Variable(POP) | ||||
| IDH | GDP_PC | GDP | ||
| NU | 0,793 | 0,848 | 0,848 | |
| (0,000) | (0,000) | (0,000) | ||
3.1 Top 500 universities
After varimax rotation, the first two components with eigenvalues over 1, which accounted for 97.8% of the total variance in the original variables, were chosen for the data considered as a whole. The indicators for the general sample characteristics were grouped in the first component and all the others in the second. Table 4 gives the percentage of the variance for each indicator explained by the two components selected.
The MLR model for the data taken as a whole yielded an adjusted determination coefficient (R2) of 73.9 %, with the ANOVA showing the model to be significant (the y-intercept was 1.72 and the component coefficients were respectively 0.037 and 0.931). The Durbin-Watson test (which measures inter-residual correlation) yielded a value of 2.077, indicating that the null hypothesis (ρ=0) could not be rejected and one of the scores for one of the principal component regressors was not significant. A robust M-estimator regression model was built for this sample using the same scores, a y-intercept of 1.78 and component coefficients of 0.042 and 0.940. Cook’s distance revealed the existence of outliers, which are shown in Figure 1 .
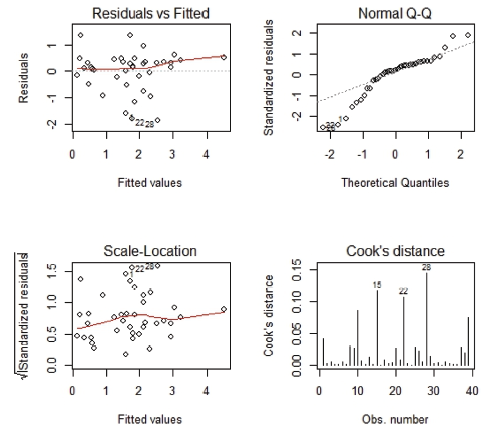
Figure 1. Outliers detected using Cook’s distance. |
The MLR model findings denoted the presence of high residuals due to the effect of possible outliers. Highly influential observations and residuals for USA, ZAF, NOR, IND, and CHN were detected and excluded and the principal components were recalculated and the first two components selected. The percentage of variance explained by the components in these new results amounted to 96.3% (Table 3 ).
Table 3 Values for each indicator by component (before excluding outliers). |
| Principal Component Analysis | ||||
|---|---|---|---|---|
| Indicator | Population | GDP | GDP PC | HDI |
| First component | -0.499 | 0.041 | 0.979 | 0.964 |
| Second component | 0.864 | 0.998 | -0.099 | -0.153 |
| % of explained variance | 0.996 | 0.998 | 0.967 | 0.952 |
Table 4 Values for each indicator by component (after excluding outliers). |
| Principal Component Analysis | ||||
|---|---|---|---|---|
| Indicator | Population | GDP | GDP PC | HDI |
| First component | -0.377 | 0.119 | 0.970 | 0.946 |
| Second component | -0.922 | -0.992 | 0.011 | 0.153 |
| % of explained variance | 0.993 | 0.999 | 0.942 | 0.918 |
Excluding data for USA, ZAF, NOR, IND, and CHN. |
The MLR model-adjusted R2 rose from 0.739 to 0.787, the p-value was highly significant (p<0.001) and the Durbin-Watson value was 1.945. In this model, the dependent variable was the natural logarithm of the aggregate indicator “number of a country/region’s ranked universities”. The y-intercept for the model estimated under these conditions was 1.692 and the regressor coefficients were 0.111 and 0.781 for the first and second component scores, respectively. Both the ANOVA and the coefficients were significant at 90%.
The exponential functions of the dependent variable were calculated to compare the values estimated by MLR to the actual number of each country/region’s ranked universities. The result is shown in Figure 2 . The regression findings can be graphically interpreted in terms of country/region positions with respect to the first quadrant diagonal. Countries/regions located above the diagonal, such as Japan, Russia, and Singapore, have fewer universities than predicted by the model on the grounds of their economic and social potential. The opposite is true for countries/regions such as United Kingdom, Germany, Spain, Italy, and France, which are located below the diagonal, for their real number of universities is higher than predicted.
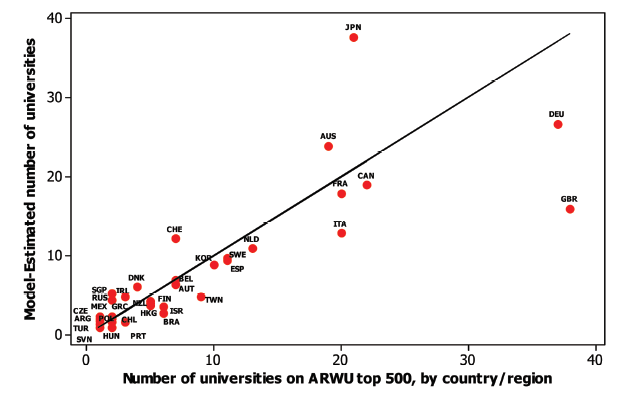
Figure 2. Actual vs MLR model-estimated number of universities on the ARWU (excluded influence observations). |
Partial regression analyses were also constructed to ascertain the individual effects of each component on the dependent variable. The second component was found to have a positive effect, with an adjusted determination coefficient of 76.9% and a Durbin-Watson value of 2.03.
A robust M-estimator regression model was built using the same scores, with a y-intercept of 1.665 and component coefficients of -0.111 and 0.773. As in the preceding case, the number of each country/region’s listed universities was estimated by applying the exponential function to the dependent variable. Figure 3 plots the original values versus the values estimated with the robust MLR method. The graphs may be interpreted as in Figure 2 : note that the country/region positions are largely the same in the two sets of figures.
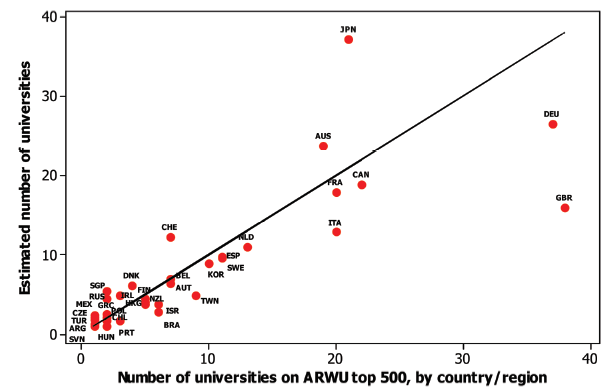
Figure 3. Actual vs robust regression model-estimated number of universities on the ARWU (excluding observations with high influence) |
When the HDI for each country/region in the ARWU top 500 was raised by 1%, the number of ranked universities did not rise in the same proportion. For some countries/regions, this change had no effect on their position on the diagonal. Examples are Mexico, Brazil, Hungary, and Poland. For others, in contrast, such as Finland, Spain, Germany, and United Kingdom, the 1% rise in HDI raised their values slightly, placing them above the diagonal (Figure 4 ).
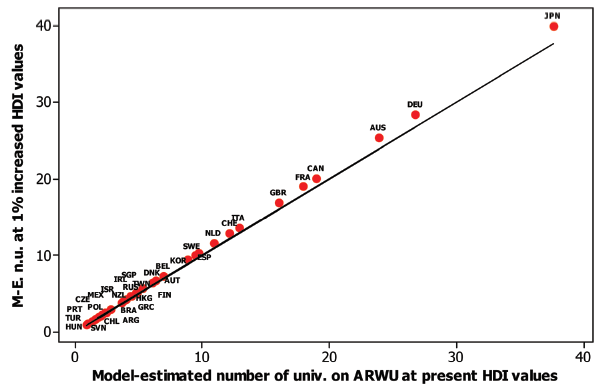
Figure 4. Model-estimated(M-E) number of universities (n.u) on ARWU before vs after raising HDI by 10%. |
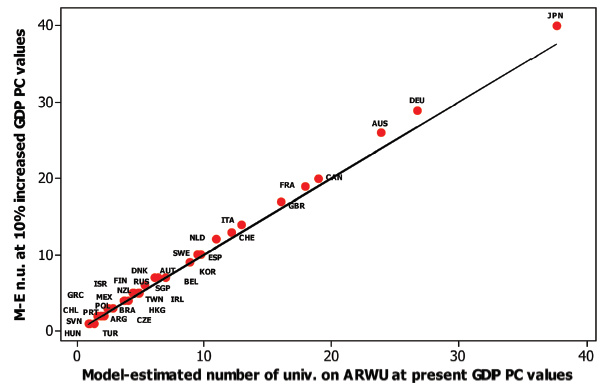
Figure 5. Model-estimated (M-E) number of universities(n.u) on ARWU before vs after raising GDP per capita by 10%. |
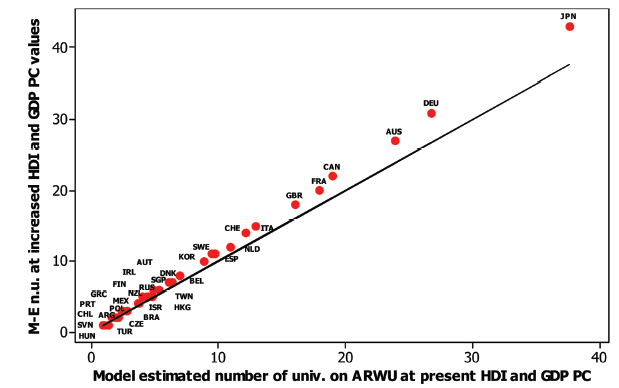
Figure 6. Model-estimated (M-E) number of universities (n.u) on ARWU before vs after raising GDP per capita and HDI by 10%. |
Lastly, the effect of variations in one of the scores on the model results was analysed. Figure 7 shows that a one-unit increase in the scores of the first component raised the model estimates by 5.7 units. For countries/regions such as Brazil, Mexico, Russia, and Spain the rises were 3, 3, 6, and 11 units, respectively. Japan and Germany, with outlying values of over 30 units, were positioned in the upper area of the figure.
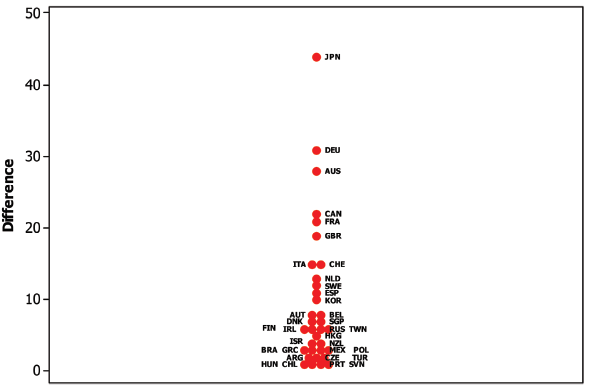
Figure 7. Point graph showing the differences between the number of universities on the ARWU when score 1 is modified. |
3.2 Top 100 universities
For the number of each country/region’s universities in the top 100, the statistical approach entailed establishing mutually exclusive sub-sets represented by dummy variables, in which the criterion was these institutions’ presence or otherwise in the top 100. This variable was analysed with respect to three new indicators in each country/region: GDP PC (greater or lesser than the median), the HDI value (very high or otherwise) and the number of universities per one million inhabitants.
The results of applying the chi-square test for relationships among these indicators are given in Tables 4 and 5. Further to the data in Table 5 , the presence in the ARWU top 100 was highly dependent on having a high GDP PC, with a very low p-value (p<0.001) for this test. The test results in the table also show that independence between presence in the top 100 and a high HDI value cannot be ruled out, however, for the p-value, at 0.093, is higher than the 5% ceiling. The null hypothesis of independence between presence in the top 100 and number of universities per million inhabitants was rejected on the grounds of Pearson’s chi-square (p=0.000; see Table 6 ), which denoted a high correlation between these two indicators.
Table 5 Effect of GDP per capita and HDI on countries/regions’ presence in the ARWU top 100 (dummy variables). |
| At least 1 university | No universities | Total | p-value | |
|---|---|---|---|---|
| GDP PC > median(GDP PC) | 14 | 5 | 19 | 0,000* |
| GDP PC ≤ median(GDP PC) | 2 | 18 | 20 | |
| Very high HDI | 15 | 17 | 32 | 0,093 |
| Other | 1 | 6 | 7 |
Table 6 Relationship between number of universities per million inhabitants and country/region presence in the ARWU top 100 (dummy variables). |
| Presence in the ARWU top 100 | ||||
|---|---|---|---|---|
| No. univ. per 1 M inhabit. | At least 1 univ. | No univ. | Total | p-value |
| more than 2 | 16 | 12 | 28 | 0.000* |
| 2 or fewer | 0 | 11 | 11 | |
| Total | 16 | 23 | 39 | |
The data on the number of universities were taken from the education authorities’ websites for some countries/regions, http://univ.cc, and http://www.iau-aiu.net/content/list-heis. |
4 Discussion and conclusions
This study analysed the socio-economic characteristics of countries/regions whose universities are listed on the ARWU from two approaches. The first consisted of representing these universities by means of a MLR model and a robust estimator, both based on principal components, while the second focused on the sub-set of countries/regions with institutions in the ARWU top 100.
Under the present assumptions, the fit to the present data set afforded by robust multiple linear regression was equivalent to the fit found with classical multiple linear regression. Only slight differences were observed in the MLR and robust MLR model results, as a comparison of Figures 2 and 3 shows. As in Safon (2013), countries/regions with long-ranking tradition such as Germany, United Kingdom, Canada, and Italy, had a larger number of universities in the top positions than predicted by the regression model. It could means that the competition among universities takes more a form of the “winners take the most” phenomenon. In contrast, for Japan, a country where social and economic performance is high, the number of ARWU universities projected by the model was much larger than the actual figure. These results were consistent with Docampo’s (2012) findings, “… suggesting that Japanese higher education system might have began to fall into decline in the past decade”. As in Docampo (2012), in this study the university systems in three Asia-Pacific countries/regions, namely Chinese Hong Kong, New Zealand, and Chinese Taiwan, were found to show good performance. Countries/regions such as Spain, Sweden, and The Netherlands exhibited higher real than predicted values, although as shown in Figures 2 and 3, they were close to the 45° regression line representing the expected behaviour further to the MLR model and a robust estimator.
Countries/regions with heavy investment in education, such as Japan and Denmark, had lower than expected results: i.e. in light of their social and economic status, they could intensify their presence on the ARWU.
Conclusions may also be drawn from the adjusted regression model estimates on how changes in the original variables might translate into improvements in positions on rankings. To that end, the effect of a change in the indicator on the response variable was studied assuming constant mean and variance, the statistics used to standardise the indicators in the principal component extraction phase.
When the HDI for each country/region in the ARWU top 500 was raised by 1%, the number of universities making the cut did not rise in the same proportion in all countries/regions. The values for some countries/regions, including developing nations such as Mexico, Brazil, and Turkey, as well as Hungary, Poland, and Portugal, remained unaltered. In other cases, the values rose only slightly, such as in Finland, Israel, Korea, and Spain. Growth in that number was proporionally higher in United Kingdom, Germany, Canada, Italy, France, Australia, and Japan.
When GDP per capita was raised by 10%, the number of universities estimated by the model to be included in the ranking failed to rise for certain countries/regions with per capita GDP below the median, such as Portugal, Argentina, Mexico, and Brazil. The number grew only slightly in some countries/regions with HDI and GDP per capita higher than the median, including Switzerland, New Zealand, and Finland. In contrast, according to the model findings, United Kingdom, Germany, France, and Australia would be positively impacted, i.e. the number of their universities expected to be on the ranking would climb.
When both welfare indicators were raised by 10%, most countries/regions exhibited significant rises in the presence of their universities on the ranking, especially countries/regions with the most favourable socio-economic conditions, such as United Kingdom, France, Germany, Canada, Australia, and Japan. Under these circumstances, the number of universities estimated by the MLR model remained unchanged only in Slovenia, Turkey, Hungary, and Argentina.
Similarly, the effect of altering the value of one of the principal component scores on the MLR model was also analysed: when that score for HDI and GDP per capita rose by one unit, the presence of each country/region’s universities on the ARWU rose by more than eight units.
To study the characteristics of the countries/regions with universities on the ARWU in greater depth, the focus was shifted to countries/regions with universities listed among the top 100, regarding this position to be an indicator of quality and excellence. To that end, a dummy variable was defined to separate the countries/regions analysed on the grounds of their presence or otherwise in this special sub-set. The analysis was inspired by the premise of Bornmann, Mutz, and Daniel (2013) to the effect that countries/regions with more abundant resources (GDP per capita) for implementing high quality projects may also have higher scientific research indicators, which are essential to positioning their universities at the top of the ARWU. Those authors also contend that the larger the number of universities engaging in research in a country/region, the more papers of excellence it produces. That, in turn, would favour their presence among the top 100.
According to Docampo (2008), the ARWU prioritises scientific research over reputation, where the dummy variable is also an indicator of excellence and hierarchy, inasmuch as having universities among the top 100 means that the country/region occupies a prominent position in research. A chi-square test was run to ascertain the relationship between this indicator and HDI and GDP per capita, duly classified as dummy variables. New indicators were defined in both cases: for HDI, whether a country/region’s index was regarded as high, and for GDP per capita, whether it was higher or lower than the median (an indication of the availability of economic resources). The former was identified as an indicator of social stability and the latter of the availability of financial resources. The results revealed a relationship for GDP per capita, but not for HDI. Further to those findings, a greater abundance of resources would favour the presence of universities in higher positions.
To verify the second premise put forward by Bornmann, Mutz, and Daniel (2013), a test was run to ascertain the existence or otherwise of a relationship between the number of universities per million inhabitants and the dummy variable, i.e. the presence or otherwise of each country/region’s universities on the ARWU top 100. Pearson’s chi-square test of independence between the two indicators yielded a value of p=0.000. That would confirm the existence of a relationship between research output and the number of universities per million inhabitants. Countries/regions that prioritize higher education exhibited the highest values for these indicators.
Author Contributions
Esteban Fernandez Tuesta (tuesta@usp.br), conceived the original idea, collected the data, performed the literature review, participated in the development of methodology, wrote the manuscript and participated in the review of the final version of the manuscript; Carlos Garcia-Zorita (czori-ta@bib.uc3m.es), conceived the original idea, designed and reviewed the methodology, participated in the preparation of the manuscript, and reviewed and approved the final version of the manuscript; Rosario Romera Ayllon (mrromera@est-econ.uc3m.es), designed the methodology, discussed the statistical results and participated in the paper review process; Elías Sanz-Casado (elias@bib.uc3m.es), reviewed the research results, elaborated the conclusions, wrote the manuscript, and reviewed and approved the final version of the manuscript.