1 Introduction
The Integrative Levels Classification (ILC) is a recently developed knowledge organization system (KOS) that includes innovative features. Gnoli (2020) provides a general description of ILC with further bibliography.
While being inspired by traditional bibliographic classification schemes, it lists phenomena instead of disciplines, which makes it suitable for organizing any kind of documents, including museum specimens or digital information. Classes of phenomena are arranged according to the theory of levels of reality (Hartmann 1952), claiming that a series of levels of increasing organization can be identified in the real world, such that higher levels (e.g. consciousness) depend on lower ones (e.g. organisms) for their existence, but at the same time have emergent properties that cannot be found in lower levels (e.g. self-awareness). The series of ILC main classes is thus one of increasing organization, from the most primitive mathematical and physical entities to the most evolved achievements of human cultures (Gnoli, 2017a; Kleineberg, 2017):
a forms
b spacetime
c branes
d energy; wave-particles
e atoms
f molecules
g continuum bodies
h celestial bodies
i rocks
j land
k genes
l bacteria; prokaryotes
m organisms (eukaryote)
n populations
o instincts
p consciousness
q language
r rituals
s communities
t polities
u enterprises
v technologies
w artefacts
x artworks
y knowledge
The first edition (ILC1) was published in 2011 and included 7,052 classes and facets. A new edition (ILC2) has been published in 2019, which includes 10,851 classes and facets. ILC2 is available at the ILC project website (http://www.iskoi.org/ilc/) through a browsable PHP interface as well as in SKOS format.
Like any KOS in its first years, ILC evolves at a relatively quick pace, as a result of progress in research as well as feedback from testing it with actual applications. This paper focuses on the transition from ILC1 to ILC2, by illustrating the main changes that have been introduced in ILC2 and the theory behind them. Sections 2 and 3 concern changes in the list of main classes and relevant developments within some of them, especially mathematics. Section 4 concerns some changes in the fundamental categories on which facets are based. Section 5 concerns the notation for special facets as opposed to that for common facets, and their distinction from “attributes”. Section 6 briefly informs about publication in SKOS format, which will be the object of other papers. Section 7 discusses ongoing application to the BARTOC directory.
2 Rearrangement of some main classes
The sequence of ILC main classes has not changed much in its second edition. It is now acknowledged that such 25 levels can be grouped in some major “strata” as in Nicolai Hartmann’s version of levels theory: information (a-c), matter (d-j), life (k-n), mind (o-p) and culture including society (q-v) and cultural products (w-y).
A major change is that ILC1 class z “wisdom”, which included spirituality and religions, has been moved to r with the new label “rituals”, also including other celebrations and traditional expressions of human societies. The alternative between an anthropological and a spiritual-intellectual placement of religions, whose nature include aspects of both, is an old dilemma in classification: it is indeed acknowledged explicitly in the Bliss Bibliographic Classification, 2nd edition, which leaves users free to choose either option. Placement of “wisdom” at the end of ILC1 main classes, viewed as the most integrated achievement of human spirit, had an equivalent in Dahlberg’s Information Coding Classification.
After its move to r in ILC2, z is not used anymore as a main class, and this digit remains reserved only to the function of expanding notation for other classes (emptying digit). This device can also be applied to main classes that are not yet prominent though being conceptually fundamental, as done for czp “preons” which follows c “branes”: both of these entities are theorized in fundamental physics and are in wait of future developments in research. It seems reasonable to provide for free notational space in this region, as substantial developments in knowledge are expected in the coming decades.
In ILC1, r was used for languages, which are now moved to q, with individual languages listed under qv. Notation q was previously used for other forms of animal communication, much used in the early application to the BioAcoustic Reference Database, which are now subsumed under animal behaviour (“instincts”) in o. Another local move is that of minerals and rocks from subclasses of j “land” in ILC1 to their own class i in ILC2. Notation i was previously occupied by weather which is now an attribute of j, in an attempt to have main classes better reflecting actually different levels of organization (land is now seen as a level emerging from rocks) rather than just aspects of a same level (weather is seen as an attribute rather than an autonomous level).
3 Development of class a “forms”
Among others, class a “forms” has been largely developed with the addition of various mathematical entities and their facets. Classes of algebraic structures have thus been outlined in greater detail, and several new classes have been introduced, mostly pertaining to the domains of abstract algebra, topology and combinatorics. The new class ak “spaces” includes various kinds of geometrical spaces like vector, affine or topological spaces. The class al “algebraic structures” gathers objects ranging from general algebraic systems to groups, ring-like structures and categories, which were previously scattered into various subclasses of a. Also, a new class am “combinatorial structures” has been defined in order to contain discrete mathematical objects, such as partially ordered sets and graph-like structures.
The main efforts in the expansion and development of the classification of mathematical structures have been conducted in order to reach an equilibrium between conflicting necessities, trying to maximize usability (both for the indexer and the user) while keeping the whole system as mathematically sound as possible.
Regarding mathematical soundness, we shall recall that all objects in mathematics are, ultimately, just sets. An ideal KOS for mathematical objects, reflecting the real technical nature of abstract structures in terms of sets, would become an extremely complicated system, which would appear practically unusable: in such a system, even common mathematical concepts would have extremely long and complex notations. Therefore, we had to acknowledge the unsuitability of such a perfect representation and accept some compromises in our classification.
Quite often, a given type of mathematical structure may be defined as a set endorsed by a family of properties: this leads to some problems when trying to include such objects in a KOS, as there is no a priori principle indicating in which order those properties shall be taken into account when defining their respective branchings. Occasionally, some properties can be seen as mathematically more fundamental than others, thus having a bigger priority and causing a branching at a prior rank of specificity, but most often there is no clear preference.
A related issue regards the uncertainty of the place of definition, as some structures may be well defined in different places in the tree. ILC endorses the principle of unique place of definition, so we had to choose only one spot for each structure type. By means of semantic factors it is nonetheless possible to indicate the semantical dependence of a concept with respect to another one defined in a different place in the schedules, thus keeping track of the ambiguity without loss of information.
Construction of classes for quantities and for dates is now possible by letters that stand for negative or positive digits in the same array and produce a correct ordering:
anad numerals, decimal digits
anade -9
anadf -8
anadg -7
...
anadm -1
anadn -0 [zero in negative numbers]
anado 0
anadp 1
anadq 2
anadr 3
anads 4
anadt 5
anadu 6
anadv 7
anadw 8
anadx 9
anq [anad] thousands
anqp one thousand
anqpxor 1903
These digits can be reused to construct dates, as well as to identify persons (in a way similar to Colon Classification) by their birth time:
rab [anad] historical periods
rabpxor year 1903 Common Era
U [anad] persons by birth time
Upxor persons born in 1903 CE; Konrad Lorenz; John von Neumann
4 Facet categories
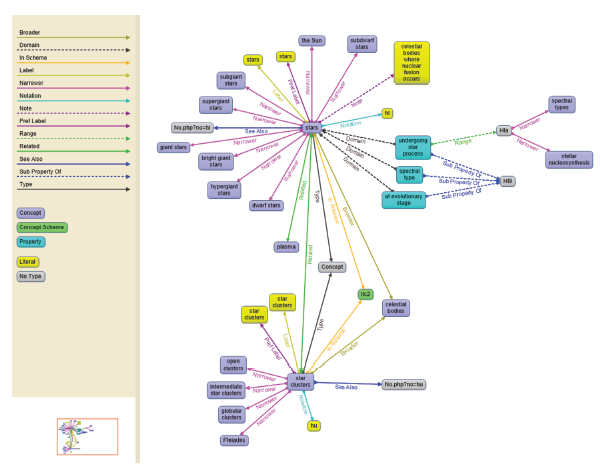
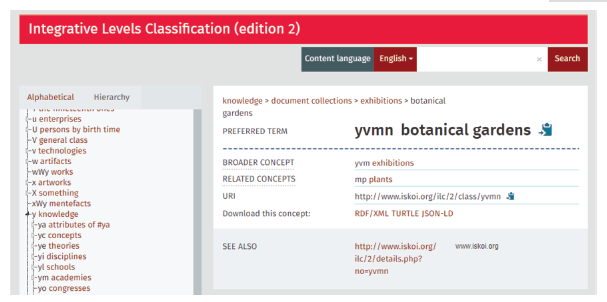
Facets of ILC are based on a system of ten fundamental categories, expressed with digits 0 to 9, analogous to Colon’s “PMEST” or to Vickery’s (1975) standard citation order. As compared to these classical orders in faceted classification, the system of ILC1 was original in several respects, like expressing agents in an “origin” category (6) that filed after processes (3). After experience with ILC1 and reconsideration in light of general systems theory (Bertalanffy 1968; Foskett 1980), in ILC2 the citation order of categories is someway more traditional, with agents in 3 and processes in 5 (now labeled by the more general term “transformation”, which also holds for mathematical and geometrical entities). Details of these changes are discussed in Gnoli (2017b).
A remarkable innovation of ILC2 is the original category of “disorder” introduced at 4, covering e.g. the disease facet in organisms and the failure facet in artifacts. This has been inspired by Edgar Morin’s (1977) philosophy of complexity, according to which all real systems are the result of an equilibrium between constructive and destructive factors - a fact often ignored in other views of levels, that depict them as a triumphal, one-directional march towards organization that is probably exceedingly idealistic. Indeed, much of human knowledge to be classified concerns problems and ways to face them, like in medicine or in management. This can be seen as an aspect of general systems theory, that considers all entities as systems composed of parts and links between them, which is another source for the identification of facet categories. Indeed, systems theory and levels theory can be combined fruitfully in consistent treatments, like that of Bunge (2003).
5 Free facets, special facets and attributes
In its most simple application, ILC allows for relevant concepts to be simply juxtaposed, as in mq nyr “animals: forests”. This application can be useful for quick indexing of a general collection of, for example, webpages, videos, or books.
Specialized collections like those of a domain bibliography may need more detailed expression of relationships between concepts, which can be performed by ILC facets. ILC has both free facets, that is, facets that can be applied to any class, like “large” or “in Korea”, and special facets, which make sense only within certain classes, like “walking” or “wooden”.
In ILC1, digits 0 to 9 introduced both free facets and special facets, and their meaning depended on whether a special facet for the digit on hand was defined in the schedules, and on the complex use of V as a facet neutralizer. In ILC2, the distinction has been made more clear in notation, at the price of some longer symbols. Indeed, all indicators of special facets now begin by 9, so that 91-99 introduce special facets, like mq926 “animals, living in habitat”, while 0-9 introduce the more general free facets, like 26 “within environment”.
Another improvement in the predictability of meaning from notation is that only facets that include a 9 have a shortened notation, that is have foci parallel to those of a given class as specified in the schedules (mq926r “animals, living in forests” takes its -r from nyr “forests”). This can happen not only with special facets, but also with common facets, that is free facets that include a 9 in a position other than initial: 29 “in country” takes its foci from tt “countries”.
The foci of a special facet are often context-defined. For example, wv97 “vehicles, with part” only takes its foci from the context of w artefacts themselves, as a part of a vehicle can be a gear or a wheel but not a forest or a country. Now, in ILC1 the only way to express such a vehicle part as “wheels” was wv97hh, which literally means “vehicles, with wheels”. There was no way to express wheels as an autonomous phenomenon, like occurring e.g. in the store catalogue of an auto
parts seller.
parts seller.
In ILC2, the latter meaning can now be expressed in the form of attributes of a class. Attributes are always introduced by a -a- which is not used to express subclasses anymore. Thus, wa “artefact attributes” include wahh “wheels” meant as separate from the artefacts to which they belong.
Attributes usually consist of processes, properties or parts, that are conveniently listed in this order in schedules, though not marked in any particular way for now. However, processes can often be used as foci of process facets (95), properties as foci of property facets (96) and parts as foci of part facets (97, as in wv97hh “vehicles, with wheels”).
Expression of wheels as a part using a facet (in ILC1):
w97 with organ, component, part
wv vehicles
wv97hh vehicles, with wheels [specifications of a class]
Expression of wheels as a phenomenon itself (newly added in ILC2):
w artifacts
wah mechanical components
wahh wheels as auto parts alone [attribute class]
This distinction between attributes (“wheels”) and faceted compounds (“vehicles, with wheels”) is an innovative feature of ILC as compared to other faceted classifications such as Colon or Bliss. It recognizes Brian Vickery’s (1975) conception, as reported by Coates (1988), that “facets may be characterised alternatively as categories of concepts or as a class of relationships between concepts”. The same consideration was also made by Jacques Maniez, as recently discussed by Hudon and Fortier (2018).
6 Publication as SKOS
The structure of ILC as a freely faceted classification (Gnoli et al., 2011) has been analyzed in order to publish the scheme in SKOS format. SKOS has been chosen because it currently is the standard format for representing knowledge organization systems, despite other formats like OWL that allow for greater expressivity.
While not all structural elements can be represented accurately in SKOS, most classes, captions and synonyms can indeed be published as SKOS, which has been done in collaboration with University of South Wales Hypermedia Research Unit (Binding et al., 2020). The SKOS version of ILC2 is available on the ILC project website (http://www.iskoi.org/ilc/skos.php). Using the AllegroGraff 3.3, the SKOS version of ILC2 can be visualized as follows:
Figure 1. ILC2 as SKOS visualization using AllegroGraff <http://www.iskoi.org/ilc/skos.php>. |
Visualization in Skosmos is also available on BARTOC Website by Andreas Ledl at Basel University Library.
Figure 2. BARTOC Skosmos browser <https://bartoc-skosmos.unibas.ch/ilc2/en/>. |
7 Application to BARTOC
Recent applications of ILC include indexing of the Basel Register of Thesauri, Ontologies and Classifications (BARTOC). In a previous study (Gnoli et al., 2018), ILC1 was used to classify a sample of KOSs in BARTOC. We assigned ILC1 class numbers in a freely combined way to 200 top-rated KOSs plus KOSs of the healthcare domain. By classifying the KOSs in BARTOC with ILC, we could compare the discipline-based DDC with the phenomenon-based ILC and analyze the knowledge dimensions of KOSs in BARTOC (Gnoli, Park, & Ledl, 2019). In accordance with the revision of ILC, ILC2 will be applied to the classification of KOSs in BARTOC.
Reclassification of KOSs in BARTOC can be done in two ways. The first way is to use a mapping table of ILC1 and ILC2. The class numbers of ILC1 applied to BARTOC are basic numbers listed in the ILC1 schedule, without facet indicators or combination of class numbers. Therefore, automatic reclassification is basically possible using mapping information between ILC1 and ILC2 classification scheme. In this process, not only the subclass numbers but also the main class numbers can be changed. For example, the KOS, Thesaurus of Clinical Signs is classified at mq30 “disease” and sh “health care” in ILC1. In ILC2, the class number becomes mqad “diseases” and vm “health care.”
The first method is effective when the classmarks in ILC1 and in ILC2 are mapped in a 1:1 way. However, as ILC2 is revised, new classes are often created or subdivided. Therefore, it may be necessary to manually assign new classmarks in accordance with ILC2. The classmarks below are some examples of 1: N mapping between ILC1 and ILC2.
Therefore, in this case, we can reclassify the KOS, International Migration and Colonization, by assigning new ILC2 classmarks after the analysis of the KOS characteristics. The KOS is classed at n3m “migration” and sx “organized civil society” in ILC1. In ILC2, it will be classed at sar “human migration” and so “organized civil society.”
8 Discussion
We have reviewed the main changes introduced in ILC2 as compared to ILC1. These concern various areas, from specific classes and subclasses to general syntactical devices for expressing attributes and faceted combinations. Finally, we have shown how changes in classes can affect reclassification of BARTOC items, and evaluated some possible methods to perform it.
We believe that these cases can provide a useful example of how a general KOS with a yet young history can evolve in time. One challenge of this process clearly is conciliating freedom in experimenting new solutions with need of stability for test applications. Indeed, one can not wait until the system is “finished” before applying it, as applications are part of the feedback process that informs the evolution of the system itself. Our paper has tried to document various such changes that have been introduced in ILC2 in the very last years, both to keep track of them and to illustrate a process of KOS evolution between experimentation and stability.
Author contributions
Ziyoung Park (zgpark@hansung.ac.kr) analyzed the application ILC to BARTOC, derived reclassification implications of ILC2 development, reviewed the paper. Claudio Gnoli (claudio.gnoli@unipv.it) conducted the introduction and theorical foundation, analyzed the characteristics of ILC2, and made a major revision to the draft. Daniele P. Morelli (netherself@gmail.com) conducted a major revision to the field of mathematics in ILC2 and review the paper.