1 Introduction
2 Literature review
3 Methodology
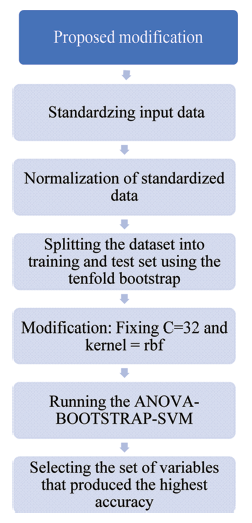
Figure 1. The ANOVA-BOOTSTRAP-RBF-SVM: illustration. |
4 Empirical results
Table 1 Maldonado et al.’s results on WBCD (Mixed linear integer approach). |
| ACC | AUC | k | Error rate | |
|---|---|---|---|---|
| l2-SVM* | 97.900 | 97.300 | 31 | 2.1 |
| LP-SVM* | 97.200 | 96.500 | 31 | 2.8 |
| l1-SVM* | 97.500 | 97.200 | 31 | 2.5 |
| Fisher+ SVM* | 97.900 | 97.300 | 31 | 2.1 |
| RFE-SVM* | 97.900 | 97.300 | 23 | 2.1 |
| l0-SVM* | 97.900 | 97.300 | 16 | 2.1 |
| MILP1* | 98.100 | 97.700 | 26 | 1.9 |
| MILP2* | 97.900 | 97.300 | 17 | 2.1 |
Source: Maldonado et al., 2014; error rate—author’s calculations. |
Table 2 Khairunnahar et al.’s results on WBCD (sigmoid classification function). |
| ACC | AUC | k | Error rate | |
|---|---|---|---|---|
| Classical system | 95.708 | 82.000 | 12 | 4.3 |
| Proposed sigmoid | 97.425 | 90.000 | 12 | 2.6 |
| Classical system | 95.423 | 97.540 | 31 | 4.6 |
| Proposed sigmoid | 96.831 | 99.000 | 31 | 3.2 |
Source: Khairunnahar et al., 2019, error rate—author’s calculations. |
Table 3 Vrigazova’s results on the WBCD. |
| ACC | AUC | k | Error rate | |
|---|---|---|---|---|
| ANOVA-CV-RBF-SVM | 97.310 | 99.750 | 3 | 2.7 |
| ANOVA-Bootstrap-L-SVM* | 97.270 | 99.131 | 24 | 2.7 |
| ANOVA-Bootstrap-RBF-SVM | 97.561 | 99.477 | 27 | 2.4 |
| ANOVA-PCA-Bootstrap-L-SVM* | 95.985 | 99.221 | 27 | 4.0 |
| ANOVA-PCA-Bootstrap-RBF-SVM* | 92.908 | 99.445 | 3 | 7.1 |
| Classical SVM with linear kernel C=1 | 97.540 | 99.990 | 30 | 2.5 |
| Classical SVM with RBF kernel C=1 | 97.720 | 99.990 | 30 | 2.3 |
| Classical SVM with linear kernel C=0.10 | 97.890 | 99.941 | 30 | 2.1 |
| Classical SVM with RBF kernel C=0.10 | 94.550 | 99.059 | 30 | 5.5 |
Source: *—Vrigazova & Ivanov, 2019, the rest is authors’ calculations. |
Table 4 Performance of modified classifications on the WBCD. |
| ACC | AUC | k | Error rate | |
|---|---|---|---|---|
| LR with bootstrap | 97.362 | 99.494 | 30 | 2.6 |
| DT with bootstrap | 92.085 | 92.458 | 30 | 7.9 |
| SVM bootstrap | 97.070 | 99.451 | 30 | 2.9 |
| KNN bootstrap | 96.159 | 98.082 | 30 | 3.8 |
| ANOVA-Bootstrap-RBF-SVM C=5 | 98.561 | 99.425 | 27 | 1.4 |
| ANOVA-Bootstrap-RBF-SVM C=7 | 98.201 | 99.412 | 30 | 1.8 |
| ANOVA-Bootstrap-RBF-SVM C=13 | 98.221 | 99.088 | 21 | 1.8 |
| ANOVA-Bootstrap-RBF-SVM C=14 | 98.276 | 99.648 | 27 | 1.7 |
| ANOVA-Bootstrap-RBF-SVM C=30 | 98.913 | 99.445 | 24 | 1.1 |
| ANOVA-Bootstrap-RBF-SVM C=32 | 99.627 | 98.808 | 27 | 0.4 |
Source: authors’calculations. |
Table 5 Time comparison of SVMs’s versions on the WBCD. |
| Time | |
|---|---|
| l2-SVM | 0.20 |
| LP-SVM | 0.10 |
| MILP1-NFS | 0.20 |
| MILP2-NFS | 0.30 |
| Fisher + SVM | 0.20 |
| l1-SVM | 0.40 |
| RFE-SVM | 0.40 |
| l0-SVM | 0.50 |
| MILP1-FS | 0.20 |
| MILP2-FS | 0.20 |
| ANOVA-CV-L-SVM | 0.04 |
| ANOVA-CV-RBF-SVM | 0.05 |
| ANOVA-Bootstrap-L-SVM | 0.05 |
| ANOVA-Bootstrap-RBF-SVM | 0.07 |
| ANOVA-PCA-Bootstrap-L-SVM | 0.07 |
| ANOVA-PCA-Bootstrap-RBF-SVM | 0.06 |
| Classical SVM with linear kernel C=1 | 0.65 |
| Classical SVM with RBF kerne C=1 | 0.95 |
| Classical SVM with linear kernel C=0.1 | 0.55 |
| Classical SVM with RBF kernel C=0.1 | 1.02 |
Source: green—Maldonado et al., 2014; authors’ calculations. |
Table 6 Comparison of the ANOVA-BOOTSTRAP-RBF-SVM performance and the classic ANOVA-SVMs with cross validation. |
| Algorithm | Datset | Kernel | C | ACC | AUC | N of features | Error rate |
|---|---|---|---|---|---|---|---|
| ANOVA-BOOTSTRAP- RBF-SVM | WPBC | rbf | 30 | 85.4 | 71.9 | 20 | 14.6 |
| rbf | 5 | 82.3 | 70.3 | 26 | 17.7 | ||
| rbf | 7 | 84.5 | 71.0 | 20 | 15.5 | ||
| rbf | 13 | 83.7 | 71.5 | 26 | 16.3 | ||
| rbf | 14 | 87.8 | 75.8 | 23 | 12.2 | ||
| rbf | 32 | 84.6 | 71.9 | 26 | 15.4 | ||
| Mamographic Mass dataset | rbf | 5 | 83.3 | 83.5 | 4 | 16.7 | |
| rbf | 7 | 81.5 | 83.5 | 4 | 18.5 | ||
| rbf | 13 | 82.4 | 83.7 | 5 | 17.6 | ||
| rbf | 14 | 82.5 | 83.7 | 5 | 17.5 | ||
| rbf | 32 | 84.5 | 83.7 | 5 | 15.5 | ||
| rbf | 30 | 81.7 | 83.8 | 3 | 18.3 | ||
| Classic ANOVA SVMs with tenfold cross validation | WPBC | rbf | 30 | 78.5 | 71.7 | 26 | 21.5 |
| rbf | 5 | 74.6 | 69.1 | 3 | 25.4 | ||
| rbf | 7 | 74.9 | 69.1 | 3 | 25.1 | ||
| rbf | 13 | 75.1 | 69.1 | 23 | 24.9 | ||
| rbf | 14 | 75.4 | 69.1 | 30 | 24.6 | ||
| rbf | 32 | 78.5 | 71.7 | 26 | 21.5 | ||
| Mamographic Mass dataset | rbf | 5 | 78.7 | 85.8 | 3 | 21.3 | |
| rbf | 7 | 79.0 | 85.9 | 3 | 21.0 | ||
| rbf | 13 | 79.5 | 86.4 | 4 | 20.5 | ||
| rbf | 14 | 79.6 | 86.3 | 4 | 20.4 | ||
| rbf | 32 | 80.0 | 87.0 | 5 | 20.0 | ||
| rfb | 30 | 80.1 | 86.9 | 5 | 19.9 |
Source: author’s calculations. |