1 Introduction
The researchers’ impact is a quantitative representation of the number of papers and citations. The most well-known index for a researcher’s impact is called the H-Index, proposed by Hirsch (2005), which combines two parameters, i.e. the number of papers and citations. Most indexing services i.e. Scopus, Clarivate Analysis, and Google Scholar use H-index to represent the researcher profile.
From the literature, H-index is used because it has advantages such as 1) it has a simple mathematical calculation, 2) it combines the number of papers and citations, 3) it can be applied at any levels, 4) high citation number for several papers did not affect the H-index value of a researcher, 5) all types of documents can be included, 6) uncited papers have no effect on the H-index value, 7) the total output of publication is correlated with the H-index value (Jin et al., 2007). The disadvantage of the H-index is that the high number of citations from several papers cannot increase the H-index value (Egghe, 2006). It does not accommodate researchers that have a high number of citations from several papers and the number of papers that have a few numbers of citations. (Gagolewski & Grzegorzewski, 2009). H-index calculation does not take into account the group of researchers, which has an “infinitely many” citations on the n number of papers, and the rest of the other papers that have n number of citations (Mesiar & Gagolewski, 2016).
Many researchers have proposed some H-index variants to fix or complement the H-index, i.e. G-index (Egghe, 2006), Maxprod (Kosmulski, 2007), AR-index (Jin, 2007), and HCP-index (Waltman, Van Eck, & Wouters, 2013). The correlation study between H-index and its variant has been done with the correlation value of H-index and its variant of 0.8 to 0.9 (Bornmann et al., 2011). There is no significant difference between the variants compared to H-index, so the H-index is still used.
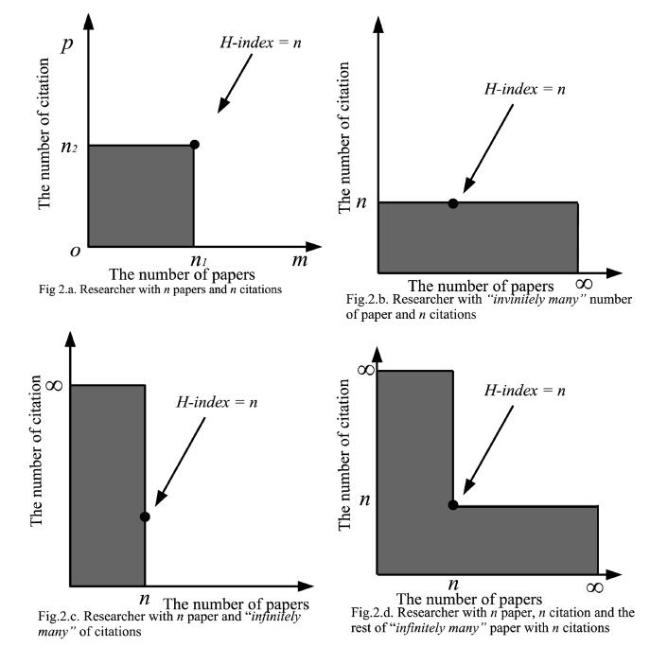
One of the problems is some institutions still use the H-index for evaluative purposes, for example, the H-index is used to evaluate the ranking of an academic department (Meyers & Quan, 2017). It’s difficult to differentiate two or more institutions/scientists who have the same H-index, so it cannot be distinguished by the impact factor. This is one of the lack of the H-index (Zhang, 2013). The rank of the top world researchers is based on the H-index, but one needs to differentiate researchers with the same H-index, for example, an implementation of the rank of scientists on the webometrics website (Aguillo, 2018; Mester, 2016). The problem occurs because the H-index is a single number indicator, so it is possible to find researchers with the same H-index. 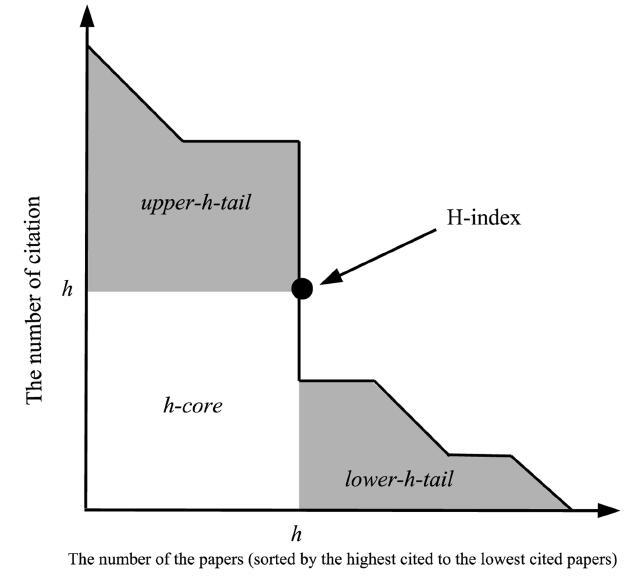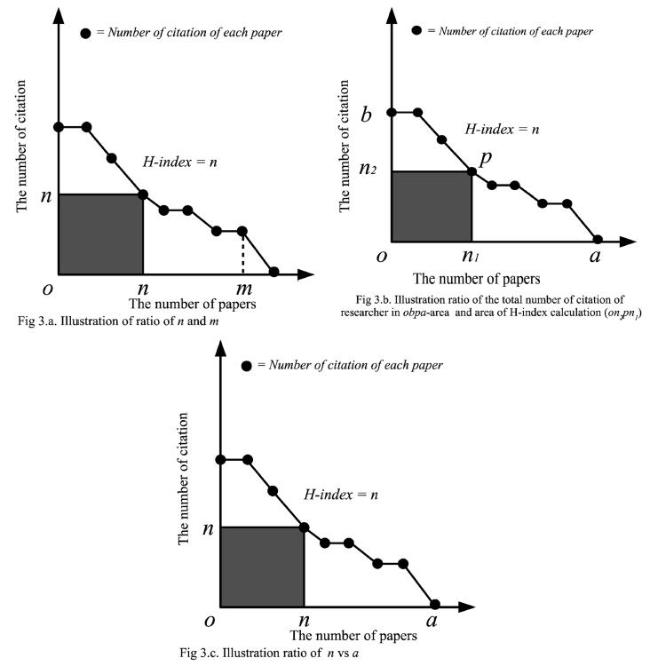The cause is due to the loss of citation information on the H-index calculation (Zhang, 2013). The loss of citation information on the H-index calculation is due to the high number of citations from some papers and the number of citations of papers that have the number of citations under the H-index value are not calculated by H-index method (Zhang, 2013).
The area of the loss of citation information is located in upper-h-tail and lower-h-tail of the citation distribution graph. Figure 1 shows the areas of the loss of citation information.
Figure 1. Upper-h-tail and lower-h-tail were not considered in the H-index calculation. |
In addition to the loss of citation information, the number of uncited papers was not considered calculation of H-index. Thus, the paper that has no citation is considered in as same as the paper that is not existed, indexed and published. The information about the number of uncited papers is potentially taken into account to differentiate researchers that have identical H-index.
To answer this question, we introduce a simple model of discrimination index. This model demonstrates that, the discriminatory value of the loss of citation information stems from the number of citations and the number of papers in the upper-h-tail and lower-h-tail areas. The boundary of the discrimination value is from 0 to 1. The result of this discrimination value is tested by the correlation with H-index and other parameters. The method used is based on the Shapiro-Wilk method and Pearson’s product-moment correlation (Hauke & Kossowski, 2011). This test is important to prove whether the results of the discrimination calculations correlate with the H-index value. The purpose of this work is to find a parameter value to make the H-index able to differentiate the researchers that have the same H-index. We called the result of the discrimination calculation is the Discrimination-offset (D-offset), as a result of the discrimination index calculation.
Discrimination of index calculation is important because the loss of citation information from the H-index calculation is a valuable information. The information can be processed to be used to differentiate researchers with identical H-index values. Mesiar and Gagolewski (2016) illustrated the groups that have the H-index as shown in Figure 2 .
Mesiar and Gagolewski (2016)classified four groups of researchers who have the same H-index value: a) researchers who have n number of papers and n citations, b) researchers who have “infinitely many” number of papers and n citations, c) researchers who have n number of papers and “infinitely many” number of citations, d) researchers who have n number of papers with “infinitely many” number of citations, and it has “infinitely many” number of papers with n number of citations (Mesiar & Gagolewski, 2016).
Figure 2. |
To develop a measurement tool for distinguishing researchers with same H-index values, this paper defined some areas on H-index calculation, i.e. h-core and h-tails. To distinguish the researchers with same H-index value, we use discrimination index calculation model. The model analyse three areas of the number of citations (y-axis) and papers (x-axis), which is based on the Jain’s fairness index. In this paper, three areas and parameters i.e. 1) h-core, 2) upper-h-tail and 3) lower-h-tail (Kuan, 2011; Zhang, 2013), and 4) the number of uncited papers. Figure 1 shows the area of the H-index calculation. H-tails are excluded from the H-index calculation.
This paper is divided into five sections. The next section discusses the methodology used. The third section presents data sources and data collection. The fourth section explains results and discussion. Finally, the conclusion is presented.
2 Methodology
This section has covered methodology for calculating the discrimination index and the validation test of D-offset. Data source in this study is data from the Scopus database. This study uses Scopus because the coverage is wider than Clarivate analytics (Harzing & Alakangas, 2016) and the data provided is relatively more valid than Google Scholar (GS) (López-Cózar, Robinson-García, & Torres-Salinas, 2014).
The proposed discrimination index method is described as follows:
1. Getting data set citation of the authors from Scopus database.
2. Calculating the H-index.
3. Calculating the total number of citations, the number of cited papers and the number of indexed papers.
4. Calculating the discrimination offset of authors.
5. Validating the test result of D-offset based on Pearson Product-Moment Correlation Coefficient.
6. Representing the results.
In order to provide the figure of the discrimination for this work, a calculation comparison sample of the H-index calculation value is used. The parameters to be compared are the number of cited papers, the total number of citations, and the number of papers.
The definition of fairness index here is perceived as a factor of fairness received and then represented into a number of properties (Jain, Chiu, & Hawe, 1984). Fairness index can be calculated as follows.
Jain’s method measures the fairness index of resources allocation. The resources in this paper are as the parameters to evaluate the fairness of H-index of the information distribution, i.e. the total number of citations, the total number of indexed papers and the number of cited papers.
$f(x)=\frac{[\sum^{n}_{i=1}x_{i}]^{2}}{N\sum_{i=1}^{n}x_{i}^{2}}\text{where}\ x_{i}\geq 0$
Jain’s method was chosen since it can be implemented on unlimited data and has an independent scale as the unit of measurement by bounded value of 0 to 1. It also has the continuous characteristic that can be presented by the percentage. The method can detect the slightest changes (continuous) that are appropriate to be applied to measure the discrimination value.
To improve the sensitivity of comparison of the researchers with the same H-index, the following three parameters have been considered:
a) The first parameter (α) is the ratio of the number of cited papers of researcher (m) and the number of cited papers of H-index (n), as shown in Figure 3 .a.
Figure 3. Illustration of α, β, and γ to calculate the D-offset. |
b) The second parameter (β) is the ratio of the total number of citations of researcher in obpa-area and area of H-index calculation of on2pn1, as shown in Figure 3 .b.
c) The third parameter (γ) is the ratio of the number of indexed papers of a researcher (a) and the number of indexed papers based on H-index calculation (n), as shown in Figure 3 .c.
Discrimination index can be defined as:
Discrimination = 1-Fairness Index
Resources’ allocation in this work consists of 1) the index value, 2) the number of the cited papers, and 3) the sum of the number of citations (NoC).
The sum of the number of citation = NoC -1 NoC - 2... NoC - i
$\textit{The sum of the number of citation }= \sum_{n=1}^{i} NoC_n$
We proposed some parameters for calculating the discrimination index as follows:
1. αo is the square of the H-index value, and αt is a total number of citations of a researcher.
2. βo is the number of papers of the H-index calculation, and βt is the number of papers of researcher.
3. γt is the total number of the cited papers of a researcher, and the number of cited papers in H-index calculation is γo. It depends on the H-index value, for example γo = 3, the number of cited papers based on H-index calculation is 3. Likewise, γo = 10, so the number of the cited papers based on the H-index calculation is 10.
Discrimination index can be calculated as: (Rochim, Muis, & Sari, 2017, 2018)
α = αt / αo
β = βt / βo
γ = γt / γo
$\textit{Discrimination index}=1-\left(\frac{|\alpha+\beta+\gamma|^{2}}{3*(\alpha^{2}+\beta^{2}+\gamma^{2})}\right)$
2.1 Validation testing of discrimination index calculation
The validation test is used to find the parameters’ correlation in D-offset calculation. Correlation of each parameter was obtained using Pearson’s product-moment correlation method (Hauke & Kossowski, 2011). The method is suitable to find correlations of the parameters of the H-index values, the number of indexed papers, the number of cited papers, the number of citations, the number of uncited papers, and the D-offset value.
The initial hypothesis was that D-offset has high correlation with the parameters, i.e. the number of indexed papers, the number of cited papers, and the number of uncited papers. The importance of uncited papers is analyzed, because they may be temporarily uncited but may become a “sleeping beauty of paper” (Van Raan, 2004). Sleeping beauty of paper is a publication that goes uncited (“sleeps”) for a long time and then, almost suddenly, attracts a lot of attention (“is awakened by a prince”). Therefore, it is not wise if the number of uncited paper is not used to increase the researcher’s impact value (Abramo & D’angelo, 2014; Daraio, 2019; Lou & He, 2015).
We assume that there is no correlation between D-offset with H-index value and the total number of citations. This means that D-offset is independent; thus, D-offset can be used to complement the measurement of the H-index value.
3 Data source and collection
To prove the proposed method, we explored discrimination in the numbers of citations and papers of authors based on Jain’s fairness index. This paper uses citation data set from Scopus. Here the author names are the ones listed as the top cited researcher on the Webometrics site. The source data of the citation data set are gained from the Scopus database of 1,000 world’s top scientists of the Webometrics in August 2017.
Each query has the maximum of 200 counts with the default of 25 maximum query. The quota of the maximum query is 20,000 for seven days on the Scopus Data. The data used in this work is 1,000 of world top scientists of the webometrics before it is filtered. A query program was developed using Python language to obtain data through Application Programming Interface (API).
Scopus provides data access services through two ways as follows:
1. Accessing the web using an authenticated user password at http://scopus.com
2. Accessing via an Application Programming Interface (API) by token authentication and Internet Protocol (IP) listed by Scopus, via URL address http://api.elsevier.com. Figure 4 presents a flowchart to collect the data from Scopus.
Figure 4. Data collection flowchart. |
4 Results and discussion
The data obtained from the Scopus are filtered; i.e. H-index values ranging from 1 to 110 are required. The number of data samples processed in the calculation, obtained from each range of the H index based on the highest average number of researchers from the sample data obtained.
Next process is the calculation of D-offset. This process calculated the discrimination index value of each researcher in the range of 1 to 110.
Figure 5. Discrimination offset value on Range H-index 1 to 110. |
Table 1 Distribution of discrimination offset value in H-index Range 1 to 110. |
| Mean | Minimum | Maximum | Median |
|---|---|---|---|
| 0.16 | 0.02 | 0.73 | 0.18 |
Table 2 Correlation test results using pearson product correlation moment of total citations, the number of indexed papers, the number of uncited papers, and D-offset. |
| Parameters | H-index | Total Citation | Number of Indexed Papers | Number of Cited Papers | Number of Uncited Papers |
|---|---|---|---|---|---|
| D-offset | -0.1 | 0.05 | 0.27 | 0.24 | 0.35 |
D-offset value does not correlate with the H-index value (-0.1). Table 2 shows no correlation between H-index and Discrimination offset value, which means that the D-offset and H-index values are independent. However, these parameters are expected to be used to differentiate rankings of researchers with the same H-index.
To differentiate researchers that have the identical H-index, we proposed a discrimination offset as a complement for the H-index. For example, if a researcher A has a higher D-offset value than researcher B, and conditions A and B have same H-index value, then the H-index performance of researcher A is slighty higher than that of B, because researcher A has more citations and number of papers based upon the D-offset. Figure 6 illustrates the additional scenario of D-offset value on the H-index value.
Practical implementation of the D-offset can be described as follows. Let us consider two researchers in a case. Each researcher has an H-index value 4, but the discrimination offset value of researcher A is 21% and researcher B is 0%. The H-index for researchers can be written with the format of “H-index: D-offset”. For example, the researchers’ H-index of Researcher A is 4:0.21 and Researcher B is 4:0. It can be shown that the researcher A has a higher impact than B, because researcher A has more citations and papers. The H-index and D-offset value can differentiate researcher fairly.
Figure 6. Range of H-index of (n to n+1) to add D-offset on the H-index. |
5 Conclusion
The validation testing results showed that D-offset is not correlated with H-index of -0.1, which means the value of D-offset does not depend on H-index value. The correlations of D-offset with the number of indexed papers is 0.27, with the number of papers is 0.24, and with the number of uncited papers is 0.35. Therefore, D-offset is worthy to consider as a complementary value to add to the H-index value. If the D-offset was added in the H-index value, the H-index would have more discrimination power to differentiate the rank of the researchers who have the same H-index.
In the future, we plan to make calculation method to combine H-index and D-offset into a single number and more discriminate, so that the researchers with same H-index values can simply be distinguished.
Acknowledgments
This research was financially supported by the Ministry of Research and Technology, Republic of Indonesia through Fundamental Research Grant No. 225-98/UN7.6.1/PP/2020.
Author contributions
Adian Fatchur Rochim (adian@ce.undip.ac.id) proposed the original idea and wrote the manuscript; Abdul Muis (Muis@ui.ac.id) prepared the fairness algorithm and helped to edit the text; Riri Fitri Sari (riri@ui.ac.id) analyzed weaknesses of the h-index and reviewed the manuscript.