1 Introduction
Generally, many of the Machine learning algorithms applied to classification problems assume that the classes are well balanced. But in practical scenarios, many of the applications like credit card fraud, cancer detection, oil spills from radar images, malicious apps detection, Medical Diagnosis, and many other datasets are imbalanced, which deviates from the assumption of traditional classification algorithms. When the data is imbalanced or when the dataset has skewed class distributions, the predictive power of minority classes is under threat, and it exhibits poor prediction for minority classes.
Imbalance occurs due to rare instances (Fotouhi, Asadi, & Kattan, 2019), for example, in medical diagnosis, the cancerous patient will be minimal compared to non-cancerous patient. Since the minority class is limited, learning will be difficult for the classifier to make predictions. Many researchers suggest sampling methods as a solution for imbalanced problems. Several resources have indicated a performance improvement when the data is balanced by using sampling methods before employing classification algorithm. On the contrary, it is also suggested, in some rare cases, even without balancing original data, the classifier will be able to produce a comparable performance with balanced data. Studies show that several applications like customer churn prediction (Amin et al., 2016), autism imbalanced data (El-Sayed et al., 2016), diagnosing cancer, imbalanced health care data (Zhao, Wong, & Tsui, 2018) have been analyzed in this context. One such significant dataset is Medical appointment no-show data. The data set used for the experiment was extracted from the public dataset hosted by Kaggle (www.kaggle.com)①(① Kaggle allow user community to find and publish data sets. It allows users to build models in data science and machine learning environment. It also allows users to attend competitions and solve machine learning challenges.).
A medical hospital offers various services that need the patients to book appointments for consultation, surgery, test, etc. Though patients attend their appointments on time most of the time, 20% of the patients fail their appointments. This failure, which is called a No-Show, is vital to the medical center as it blocks other patients to book their slots. The medical hospital will prefer to reduce the no-shows by predicting earlier so that other patients can utilize those slots. In practice, for any medical problem, the patient calls the doctor, and an appointment is scheduled. When patients miss their scheduled medical appointments without cancellation, i.e. a no-show, it creates an issue to the medical department. The reservation of an appointment involves the allocation of health care providers’ time, medical equipment, room, etc. From the literature (Kheirkhah et al., 2016), it is seen that more than 20% of patients don’t show up, resulting in two fold issues such as creating a financial loss to the doctor and also it really affects the patients who need doctor appointment. This shows that data is imbalanced. Several imbalanced algorithms are available as a preprocessing technique that balances the data before we can apply the classifier.
This research aims to build a classifier to predict (Mohammadi et al., 2018) whether a scheduled appointment will be attended or not. In such a study, if any hospital data is examined, the no-show class is minimal. The application of classification algorithms on such data paves the way for inaccurate predictions since the class is imbalanced. Mostly in any training dataset, the number of instances is high for a particular class (i.e. those who do not miss their appointments), while there are few instances for other classes (no-shows). This particular scenario is called the imbalanced data. The data imbalance in the datasets could cause the resulting models to be biased towards the majority class (i.e. those who do not miss their appointments) during prediction.
Hence on the Medical Appointment No-Show dataset which is imbalanced, various under sampling and oversampling techniques were applied to make the class balanced for prior prediction. This paper also compares the performance metrics of the various over sampling and under sampling methods widely used before applying classifiers. Sampling techniques such as Random over Sampling (ROS), Random under Sampling (RUS), Synthetic Minority Oversampling Technique (SMOTE), ADAaptive SYNthetic Sampling (ADASYN), Edited Nearest Neighbor (ENN), and Condensed Nearest Neighbor (CNN) are investigated using the medical appointment no-show dataset and the Decision Tree classifier. The majority and minority class before and after sampling were found for all the chosen sampling techniques. The performance of the classifier after applying sampling was assessed using measures such as precision, recall, and Area under Curve (AUC). The performance of ENN with decision tree classifiers outperforms other techniques for the chosen medical appointment dataset. CNN and ADASYN have performed equally well on the imbalanced data.
The purpose of this paper is to balance the classes using different sampling methods for Medical appointment no-show data and identify the best results. This paper is organized as follows: Section 2 depicts the methodology adopted for Rebalancing Framework for Classification of imbalanced Medical appointment no-show data. Section 3 describes the various sampling techniques used in this experimental analysis. Section 4 focuses on the experimental setup details and the results were analyzed in Section 5. The conclusion is provided in Section 6.
2 Methodology
This paper defines a Rebalancing Framework for Classification of imbalanced Medical appointment no-show data. The data set is split into k folds, each one containing 20% of the patterns of the dataset. For each fold, data is split into training set and test set. The training data is either under sampled or oversampled to generate a balanced training sample. The decision tree classifier is applied to the balanced training data and the performance of the classifier is evaluated against the test set. This process is repeated for different sampling techniques and evaluated using performance metrics for medical no-show dataset as shown in Figure 2 . The objective is to build a prediction model which is capable of predicting whether an appointment would be no-show.
3 Sampling techniques
Data sampling provides a collection of techniques that transform a training dataset in order to balance the class distribution. Once data is balanced, standard machine learning algorithms can be trained directly on the transformed dataset without any modification. This allows the challenge of imbalanced classification, even with severely imbalanced class distributions, to be addressed with a data preparation method. There are many different types of data sampling methods that can be used, and there is no single best method to use on all classification problems and with all classification models. Sampling techniques may follow the strategy of either under sampling or oversampling.
$\bullet$ Oversampling methods, which increase the instances of minority class as equal to majority class using various techniques like ROS, SMOTE, ADASYN
$\bullet$ Under sampling methods, which reduces the majority class to minority level using various techniques like RUS, ENN, CNN
$\bullet$ Hybrid methods, which is a combination of under sampling and oversampling methods.
3.1 Random over sampling
Studies (Lemnaru & Potolea, 2012) mentions that ROS is adding examples to the minority class so that it increases the size of the minority class to balance the data. Minority class is sampled with replacement and then the samples are combined with majority data. This leads to over fitting, since it makes exact copies of existing instances. The algorithm of ROS is described below.
Algorithm 1: ROS |
| Step 1: D is the original data set Step 2: E is new set and adds it by appending randomly selected examples from the minority class (with replacement). Step 3: D = Dmin + Dmaj + E which is the balanced dataset. Dmin and Dmaj refers the minority and majority dataset respectively |
3.2 Random under sampling (RUS)
RUS is removing the examples from majority class (Galar et al., 2012) which might remove some important information. It keeps all minority data and randomly selects data from majority class which is equivalent to minority class. However, in cases where each example of the majority class is near other examples of the same class, this method might yield better results. Below depicts the RUS algorithm.
Algorithm 2: RUS |
| Step 1: D is the original data set Step 2: E is new set and it is a subset of D which is created randomly with or without replacement. Step 3: D = Dmaj + Dmin - E which is the balanced dataset. Dmin and Dmaj refers the minority and majority dataset respectively |
3.3 Synthetic minority oversampling technique (SMOTE)
ROS generates duplicate instances of minority classes whereas SMOTE generates synthetic instances of minority classes. The synthetic instances are created by joining the line segments of nearest neighbors of minority class. To identify the nearest neighbor, K-nearest neighbor is applied. The synthetic instances will be created on the line segment. This avoids the over fitting (López et al., 2013) and causes the decision boundaries for the minority class to be spread further into the majority class space. The difference between the feature vector (sample) under consideration and its nearest neighbor is taken. This difference is multiplied by a random number between 0 and 1.This calculated value is added to the feature vector under consideration. This causes the selection of a random point along the line segment between two specific features. For the nominal cases, a random instance is chosen from the k nearest neighbors and this value is assigned a synthetic variable. Each nominal attribute is repeated in this way. The disadvantage of SMOTE is that it generates synthetic data without considering nearby examples which leads to overlapping of classes.
Algorithm 3: SMOTE |
| Step 1: D is the original data set Step 2: Create data set I with minority set observation of I € D Step 3: Identify the value of K which is the number of nearest neighbors of Minority class Step 4: Identify the value of N which is the number of synthetic examples which needs to be created. Step 5: Create a dataset D’ which is the random sample of I of size N. For each example xk ∊ I D’ = x + rand(0,1) * | x - xk | |
3.4 Adaptive synthetic sampling (ADASYN)
ADASYN also improves the class imbalance by generating synthetic data like SMOTE. The ADASYN focuses on the samples which are difficult to classify (i.e. minority class with a nearest-neighbors rule) whereas SMOTE doesn’t make any distinction. SMOTE uses uniform distribution whereas ADASYN uses density distribution to identify the number of synthetic samples to be generated. ADASYN does not generate Synthetic instances for minority dataset with no majority cases in their k-nearest neighbors. (He et al., 2008).
Algorithm 4: ADASYN |
| Step 1: D is the dataset with m class examples {((x1,y1)(,(x2,y2)…..(xn,yn)} Step 2: Calculate the Imbalance ratio IR = |Dmaj / |Dmin|. If IR is less than the threshold value then the data is Imbalanced Step 3: Identify G the no of synthetic examples which need to be generated for the minority class G = (|Dmaj| - |DMin|) × β Step 4: For each instance in minority class identify the K nearest neighbor using Euclidean distance (Δi) and calculate the ration Ri which is defined as Ri = Δi /K Step 5: Normalize Ri Step 6: Identify the number of synthetic data (gi) example for each minority instance gi = ˆri × G Step 7: For each minority xi choose the nearest neighbor xk and generate the synthetic example as follows si = xi + rand(0,1) * |xi - xk| |
3.5 Edited nearest neighbour (ENN)
The ENN is another method of under sampling by deleting selected samples. It uses K-nearest neighbors to locate those samples in a dataset for deletion. All instances which have been misclassified by the k-NN rule from the training set are removed.
Algorithm 5: ENN |
| Step 1: Let D is the original training set, and T is the edited set Step 2: For each xi in D remove xk if it is misclassified using the k-NN rule |
3.6 Condensed nearest neighbour (CNN)
CNN is under sampling technique which removes the samples from its K-nearest Neighbors. A subset of data is created which will be able to correctly classify the original data set using a one nearest neighbor rule. Take a random instance from D and create a subset T. Using subset T classify the remaining elements in D which does not match class using KNN Rule. xI is randomly chosen from xn, CNN scans all members of xn, and adds to T where x of xn whose nearest prototype does not match in label with xi. The algorithm scans xn as many times as necessary, until all members of xn have been absorbed or, equivalently, no more prototypes can be added to T.
Algorithm 6: CNN |
| Step 1: Let D be the original dataset(x1,x2,x3….xn) Step 2: Take a random instance xi from D and create a Subset T Step 3: Scan all members of D and add to T where x € T does not match class using KNN Rule and add it to T. Step 4: Repeat step 3 until all members of xi have been checked |
4 Experimental setup
Imbalance Dataset: The Medical appointment dataset which is taken from kaggle website is an imbalanced binary classification problem. Sample snapshot of the no-show data set is given in below Figure 1 . The dataset contains the Appointment Id, Gender, Scheduled day, Appointment day, Age, medical details and whether the patient turned up or not turned up (No-show)
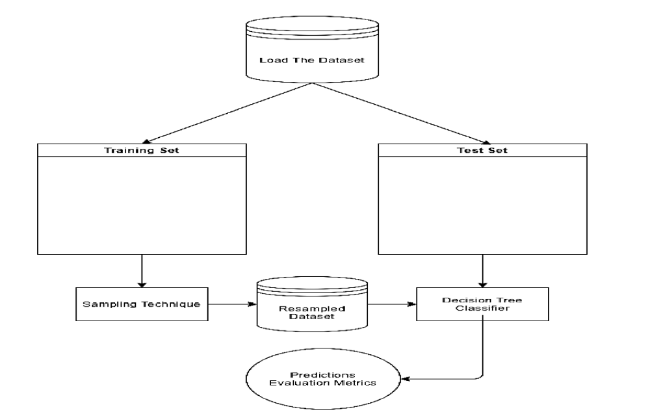
Figure 1. Rebalancing framework for imbalanced data classification. |
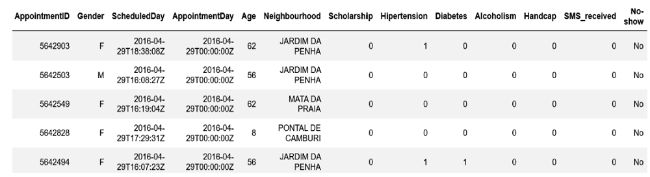
Figure 2. Sample records of medical appointment no-show dataset. |
The most important feature in the dataset is whether the patient show-up or no-show to the appointment. The structured dataset used in the modeling and evaluation is 110.527x14 dataset with 20% of minority cases and 80% majority cases where No-show and Non_no-show cases as minority and majority classes respectively. As an experimental study 8,000 records were taken and the resampling framework is applied to the data to identify the best performance of the sampling strategy.
Choice of classifier: Several Conventional classifying algorithms are available in the field of machine learning like Logistic regression, Support vector machine, Random Forest, and Decision Trees for a classification problem. The choice of classifier plays a crucial role in classifying and prediction of imbalanced data. Many healthcare applications choose the classifier based on simplicity, Interpretability and computational efficiency. In this study, Decision tree is chosen as classifier which is a non linear algorithm. This classifier is applied on the different strategies of rebalanced data for the prediction of appointment no-shows. The decision tree is identified as the appropriate classifier based on the following reasons:
$\bullet$ Successive splitting of the data space results in very fewer observations of minority class instances resulting in fewer leaves describing minority class and successively does the weaker confidence estimates.
$\bullet$ It supports weighted samples in decision trees.
$\bullet$ Decision tree does not require parameter tuning.
$\bullet$ Decision Tree performs well for both numerical as well as categorical data.
$\bullet$ The height of the tree has logarithmic complexity, the cost of accessing any tree is very less compared to other models (Mehndiratta & Soni, 2019).
Performance Metrics: The choice of metrics plays a vital role for evaluating the best sampling models for medical appointment no-show dataset. The chosen metric captures the details of a model and its predictions, which are most important to the experiment. This study concentrates on the following metric for skewed class distributions:
Recall = True Positive/(True Positive+False Negative)
Precision = True Positive/(True Positive+False Positive)
F1 Score = Harmonic mean of precision and Recall
AUCROC indicates how well the probabilities from the positive classes are separated from the negative classes.
In assessing skewed distributions, recall denotes the percentage of correctly classified minority instances. Precision means the percentage of relevant results whereas recall refers to the percentage of total relevant results correctly classified by the algorithm. F1-score represents a harmonic mean between recall and precision. In many scenarios of imbalance, recall is the primary measure which identifies rare but significant minority cases. As there is always a tradeoff between recall and specificity, indiscriminately improving recall can result in low specificity and classification accuracy.
5 Results and discussion
A 5-fold cross validation for four times was executed to get the performance metrics for 20 runs. For every fold, data is split into a training set and a test set. The training data is either under sampled or over sampled and the balanced data is used by the decision tree classifier. The performance of the classifier is evaluated against the test set in each fold. The performance measures, Recall, Precision, F1 Score AUCROC are calculated for each sampling method RUS,ROS,ADASYN, SMOTE, CNN, ENN.
In Table 1 , totally 20 trial runs were executed (RUS_TRIAL1, RUS_TRIAL2… RUS_TRIAL20), with RUS sampling method + decision tree classifier and the corresponding Recall, Precision, F1 Score, AUCROC for each trial is recorded. Similarly Table 2 to Table 6 , represents 20 trial runs of various sampling methods (ROS, ADASYN, SMOTE, CNN, ENN) + Decision tree classifier with performance measures such as Recall, Precision, and F1Score AUCROC. The comparison of sampling techniques with performance metric is tabulated in table 7. The experiment was carried out in R with UBL package.
Table 1 Random under sampling performance with decision tree. |
| Sampling method | Precision | Recall | AUCROC | F1 Score |
|---|---|---|---|---|
| RUS_TRIAL1 | 0.81934847 | 0.666132 | 0.574591 | 0.734838 |
| RUS_TRIAL2 | 0.28668942 | 0.501493 | 0.585529 | 0.364821 |
| RUS_TRIAL3 | 0.295886076 | 0.586207 | 0.619411 | 0.39327 |
| RUS_TRIAL4 | 0.851084813 | 0.677394 | 0.607102 | 0.754371 |
| RUS_TRIAL5 | 0.810810811 | 0.655226 | 0.519437 | 0.724763 |
| RUS_TRIAL6 | 0.826679649 | 0.673275 | 0.574101 | 0.742133 |
| RUS_TRIAL7 | 0.851485149 | 0.667702 | 0.593466 | 0.748477 |
| RUS_TRIAL8 | 0.866866867 | 0.679749 | 0.635887 | 0.761989 |
| RUS_TRIAL9 | 0.830491474 | 0.669361 | 0.601898 | 0.741271 |
| RUS_TRIAL10 | 0.841451767 | 0.684006 | 0.575977 | 0.754604 |
| RUS_TRIAL11 | 0.295492487 | 0.55836 | 0.614722 | 0.386463 |
| RUS_TRIAL12 | 0.273703041 | 0.496753 | 0.591256 | 0.352941 |
| RUS_TRIAL13 | 0.827420901 | 0.693173 | 0.593065 | 0.754371 |
| RUS_TRIAL14 | 0.83960396 | 0.667191 | 0.587395 | 0.743534 |
| RUS_TRIAL15 | 0.840352595 | 0.682578 | 0.603679 | 0.753292 |
| RUS_TRIAL16 | 0.281350482 | 0.589226 | 0.623086 | 0.380849 |
| RUS_TRIAL17 | 0.859683794 | 0.671815 | 0.60312 | 0.754226 |
| RUS_TRIAL18 | 0.843062201 | 0.691523 | 0.594228 | 0.75981 |
| RUS_TRIAL19 | 0.832358674 | 0.697143 | 0.619238 | 0.758774 |
| RUS_TRIAL20 | 0.81237525 | 0.650679 | 0.555999 | 0.722592 |
| RUS TRIAL MEAN | 0.699309894 | 0.642949 | 0.593659 | 0.669946 |
Table 2 Random oversampling performance with decision tree. |
| Sampling method | Precision | Recall | AUCROC | F1 Score |
|---|---|---|---|---|
| ROS_TRIAL1 | 0.853307766 | 0.696401 | 0.610623 | 0.766911 |
| ROS_TRIAL2 | 0.298611111 | 0.508876 | 0.594374 | 0.376368 |
| ROS_TRIAL3 | 0.854684512 | 0.696804 | 0.608655 | 0.767711 |
| ROS_TRIAL4 | 0.83109405 | 0.687847 | 0.585859 | 0.752716 |
| ROS_TRIAL5 | 0.847152847 | 0.669826 | 0.605871 | 0.748125 |
| ROS_TRIAL6 | 0.838461538 | 0.689873 | 0.594937 | 0.756944 |
| ROS_TRIAL7 | 0.854917235 | 0.682737 | 0.604107 | 0.759187 |
| ROS_TRIAL8 | 0.840770791 | 0.657937 | 0.598086 | 0.738201 |
| ROS_TRIAL9 | 0.853472883 | 0.700781 | 0.609766 | 0.769627 |
| ROS_TRIAL10 | 0.304878049 | 0.511696 | 0.597263 | 0.382096 |
| ROS_TRIAL11 | 0.293165468 | 0.506211 | 0.59935 | 0.371298 |
| ROS_TRIAL12 | 0.83030303 | 0.662903 | 0.598118 | 0.73722 |
| ROS_TRIAL13 | 0.850943396 | 0.70304 | 0.602309 | 0.769953 |
| ROS_TRIAL14 | 0.313559322 | 0.534682 | 0.605858 | 0.395299 |
| ROS_TRIAL15 | 0.861248761 | 0.67208 | 0.608027 | 0.754996 |
| ROS_TRIAL16 | 0.298181818 | 0.514107 | 0.60639 | 0.377445 |
| ROS_TRIAL17 | 0.844054581 | 0.687847 | 0.60932 | 0.757987 |
| ROS_TRIAL18 | 0.850551655 | 0.663537 | 0.600402 | 0.745495 |
| ROS_TRIAL19 | 0.843444227 | 0.67874 | 0.596946 | 0.752182 |
| ROS_TRIAL20 | 0.838150289 | 0.690476 | 0.598179 | 0.75718 |
| ROS TRIAL MEAN | 0.710047667 | 0.64082 | 0.601722 | 0.67366 |
Table 3 Adaptive synthetic sampling performance with decision tree. |
| Sampling method | Precision | Recall | AUCROC | F1 Score |
|---|---|---|---|---|
| ADAYSYN_TRAIL1 | 0.790373654 | 0.991263 | 0.510294 | 0.879493 |
| ADAYSYN_TRAIL2 | 0.806615776 | 0.98677 | 0.510846 | 0.887644 |
| ADAYSYN_TRAIL3 | 0.800127714 | 0.989731 | 0.526303 | 0.884887 |
| ADAYSYN_TRAIL4 | 0.804692454 | 0.987549 | 0.504885 | 0.886792 |
| ADAYSYN_TRAIL5 | 0.788973384 | 0.993615 | 0.516981 | 0.879548 |
| ADAYSYN_TRAIL6 | 0.789574062 | 0.987281 | 0.509723 | 0.877428 |
| ADAYSYN_TRAIL7 | 0.815974441 | 0.98534 | 0.518986 | 0.892695 |
| ADAYSYN_TRAIL8 | 0.805590851 | 0.987539 | 0.509592 | 0.887334 |
| ADAYSYN_TRAIL9 | 0.799492386 | 0.990566 | 0.513576 | 0.884831 |
| ADAYSYN_TRAIL10 | 0.778693722 | 0.991922 | 0.513917 | 0.872469 |
| ADAYSYN_TRAIL11 | 0.80393401 | 0.989071 | 0.51021 | 0.886944 |
| ADAYSYN_TRAIL12 | 0.790343075 | 0.992817 | 0.520904 | 0.880085 |
| ADAYSYN_TRAIL13 | 0.806883365 | 0.984448 | 0.50974 | 0.886865 |
| ADAYSYN_TRAIL14 | 0.78643853 | 0.989633 | 0.507822 | 0.876412 |
| ADAYSYN_TRAIL15 | 0.79949077 | 0.985871 | 0.509807 | 0.882953 |
| ADAYSYN_TRAIL16 | 0.792141952 | 0.993641 | 0.517288 | 0.881523 |
| ADAYSYN_TRAIL17 | 0.813095995 | 0.986122 | 0.507912 | 0.891289 |
| ADAYSYN_TRAIL18 | 0.812903226 | 0.971473 | 0.507188 | 0.885142 |
| ADAYSYN_TRAIL19 | 0.778059607 | 0.991115 | 0.512132 | 0.871758 |
| ADAYSYN_TRAIL20 | 0.789240506 | 0.991256 | 0.508786 | 0.878788 |
| ADASYN TRIAL MEAN | 0.793672332 | 0.970829 | 0.516991 | 0.873358 |
Table 4 Synthetic minority oversampling performance with decision tree. |
| Sampling method | Precision | Recall | AUCROC | F1 Score |
|---|---|---|---|---|
| SMOTE_TRAIL1 | 0.298013245 | 0.555556 | 0.611634 | 0.387931 |
| SMOTE_TRAIL2 | 0.857976654 | 0.694488 | 0.626032 | 0.767624 |
| SMOTE_TRAIL3 | 0.273462783 | 0.53481 | 0.592561 | 0.361884 |
| SMOTE_TRAIL4 | 0.8382643 | 0.669291 | 0.586161 | 0.744308 |
| SMOTE_TRAIL5 | 0.827884615 | 0.689904 | 0.590691 | 0.752622 |
| SMOTE_TRAIL6 | 0.290552585 | 0.512579 | 0.601063 | 0.370876 |
| SMOTE_TRAIL7 | 0.851669941 | 0.674708 | 0.597672 | 0.752931 |
| SMOTE_TRAIL8 | 0.842105263 | 0.666667 | 0.611742 | 0.744186 |
| SMOTE_TRAIL9 | 0.841359773 | 0.699372 | 0.592017 | 0.763823 |
| SMOTE_TRAIL10 | 0.841112214 | 0.672756 | 0.601774 | 0.747573 |
| SMOTE_TRAIL11 | 0.85257032 | 0.688332 | 0.608872 | 0.761698 |
| SMOTE_TRAIL12 | 0.310344828 | 0.49422 | 0.595595 | 0.381271 |
| SMOTE_TRAIL13 | 0.855327468 | 0.680934 | 0.605546 | 0.758232 |
| SMOTE_TRAIL14 | 0.834834835 | 0.661905 | 0.588305 | 0.73838 |
| SMOTE_TRAIL15 | 0.848393574 | 0.664308 | 0.601971 | 0.74515 |
| SMOTE_TRAIL16 | 0.303664921 | 0.494318 | 0.587303 | 0.376216 |
| SMOTE_TRAIL17 | 0.290718039 | 0.533762 | 0.609783 | 0.376417 |
| SMOTE_TRAIL18 | 0.844984802 | 0.664013 | 0.609623 | 0.743647 |
| SMOTE_TRAIL19 | 0.851887706 | 0.684825 | 0.599555 | 0.759275 |
| SMOTE_TRAIL20 | 0.846989141 | 0.675591 | 0.602947 | 0.751643 |
| SMOTE MEAN | 0.68010585 | 0.630617 | 0.601042 | 0.654427 |
Table 5 Edited nearest neighbor performance with decision tree. |
| Sampling method | Precision | Recall | AUCROC | F1 Score |
|---|---|---|---|---|
| ENN_TRAIL1 | 0.791353383 | 1 | 0.505935 | 0.883526 |
| ENN_TRAIL2 | 0.805886036 | 0.999224 | 0.502817 | 0.892201 |
| ENN_TRAIL3 | 0.796493425 | 1 | 0.504573 | 0.88672 |
| ENN_TRAIL4 | 0.799249531 | 1 | 0.501553 | 0.888425 |
| ENN_TRAIL5 | 0.780839073 | 1 | 0.504249 | 0.876934 |
| ENN_TRAIL6 | 0.793621013 | 1 | 0.501511 | 0.884937 |
| ENN_TRAIL7 | 0.787593985 | 0.998411 | 0.502138 | 0.88056 |
| ENN_TRAIL8 | 0.811166876 | 0.999227 | 0.507784 | 0.895429 |
| ENN_TRAIL9 | 0.79111945 | 1 | 0.501493 | 0.88338 |
| ENN_TRAIL10 | 0.790100251 | 1 | 0.5059 | 0.882744 |
| ENN_TRAIL11 | 0.793988729 | 1 | 0.504518 | 0.885166 |
| ENN_TRAIL12 | 0.808630394 | 1 | 0.501629 | 0.894191 |
| ENN_TRAIL13 | 0.78334377 | 1 | 0.504298 | 0.878511 |
| ENN_TRAIL14 | 0.794855709 | 0.998424 | 0.505254 | 0.885086 |
| ENN_TRAIL15 | 0.7922403 | 0.999211 | 0.501107 | 0.88377 |
| ENN_TRAIL16 | 0.805764411 | 1 | 0.506369 | 0.892436 |
| ENN_TRAIL17 | 0.778473091 | 1 | 0.502809 | 0.87544 |
| ENN_TRAIL18 | 0.80075188 | 0.998438 | 0.502344 | 0.888734 |
| ENN_TRAIL19 | 0.796875 | 1 | 0.5 | 0.886957 |
| ENN_TRAIL20 | 0.790362954 | 1 | 0.502967 | 0.882908 |
| ENN TRAIL MEAN | 0.794635463 | 0.999647 | 0.503462 | 0.885429 |
Table 6 Condensed nearest neighbor performance with decision tree. |
| Samplin method | Precision | Recall | AUCROC | F1 Score |
|---|---|---|---|---|
| CNN_TRAIL1 | 0.803154574 | 0.995309 | 0.511673 | 0.888966 |
| CNN_TRAIL2 | 0.784770296 | 1 | 0.515581 | 0.879408 |
| CNN_TRAIL3 | 0.802639849 | 0.996877 | 0.506276 | 0.889276 |
| CNN_TRAIL4 | 0.802639849 | 0.998436 | 0.510122 | 0.889895 |
| CNN_TRAIL5 | 0.791457286 | 0.998415 | 0.508083 | 0.882971 |
| CNN_TRAIL6 | 0.798865069 | 0.995287 | 0.509876 | 0.886324 |
| CNN_TRAIL7 | 0.803650094 | 0.999218 | 0.515137 | 0.890827 |
| CNN_TRAIL8 | 0.797604035 | 0.998421 | 0.517229 | 0.886786 |
| CNN_TRAIL9 | 0.792085427 | 1 | 0.511799 | 0.883982 |
| CNN_TRAIL10 | 0.797356828 | 0.998424 | 0.512807 | 0.886634 |
| CNN_TRAIL11 | 0.79886148 | 0.995272 | 0.517273 | 0.886316 |
| CNN_TRAIL12 | 0.797986155 | 0.998425 | 0.512849 | 0.887023 |
| CNN_TRAIL13 | 0.804770873 | 0.999221 | 0.509074 | 0.891516 |
| CNN_TRAIL14 | 0.789077213 | 0.998411 | 0.506537 | 0.881487 |
| CNN_TRAIL15 | 0.795725959 | 0.999211 | 0.511617 | 0.885934 |
| CNN_TRAIL16 | 0.805782527 | 1 | 0.514151 | 0.892447 |
| CNN_TRAIL17 | 0.784722222 | 0.995994 | 0.513622 | 0.877825 |
| CNN_TRAIL18 | 0.795725959 | 0.998423 | 0.509754 | 0.885624 |
| CNN_TRAIL19 | 0.811439346 | 1 | 0.514563 | 0.895906 |
| CNN_TRAIL20 | 0.790302267 | 0.996823 | 0.510142 | 0.88163 |
| CNN TRAIL MEAN | 0.797430865 | 0.998108 | 0.511908 | 0.886555 |
Table 7 Comparative study of different sampling performances with decision tree. |
| Sampling method | Precision | Recall | AUCROC | F1 Score |
|---|---|---|---|---|
| RUS | 0.69931 | 0.642949 | 0.593659 | 0.669946 |
| ROS | 0.710048 | 0.64082 | 0.601722 | 0.67366 |
| ADAYSYN | 0.789241 | 0.991256 | 0.508786 | 0.873358 |
| SMOTE | 0.680106 | 0.630617 | 0.601042 | 0.654427 |
| ENN | 0.794635 | 0.999647 | 0.503462 | 0.885429 |
| CNN | 0.797431 | 0.998108 | 0.511908 | 0.886555 |
Before analyzing the performance of various sampling methods, it is to be noted that there is no constant winner that can always beat all the other algorithms. As Recall is the key measure for an imbalanced scenario, it is identified that ENN Performance outperforms other models. It is observed that the performance of recall scales well for CNN and ADASYN also. When False Negative and False Positive are equally costly, F1 metric is significant where ENN, CNN, ADASYN outperforms others.
High Recall, Low Precision: This is achieved by ADASYN, CNN, and ENN where it has High recall and Low precision meaning the classifier were able to predict the no-shows which is a minority class more correctly.
High recall, High precision: The classifier predicts most of the positive samples where appointment has been carried out, as appointed and missed appointment as no-shows. This enables both positive and negative cases to classify correctly. RUS and SMOTE techniques perform well with High Recall and High Precision.
Moreover F1-Score which shows the prediction performance of Appointed and No-shows gives a remarkable performance when ENN, CNN and ADASYN sampling method are used with decision tree classifier.
Overall, Recall depicts the negative samples where False Negative is high where the NO_Shows were predicted correctly by sampling method using ENN.
The limitation is that the testing was carried out with a limited dataset and needs to be tested with a larger dataset and the implications are this framework will be useful whenever the data is imbalanced in real world scenarios, which ultimately improves the performance.
6 Conclusion
This experimental study incorporates various rebalancing strategies for appointment no-show data in healthcare and also some guidelines were provided for tackling similar imbalanced problems. The performance of each sampling method with Decision Tree classifier is compared. Performance is assessed with metrics such as Precision, Recall, AUCROC, and F1 score. In imbalanced classification problems, recall is usually more important since false negatives are frequently more costly than false positives. The recall value of 0.999 for ENN sampling method predicts the no-shows minority class exactly when compared to other sampling methods such RUS, ROS, ADASYN, and CNN. For future work the performance of sampling methods could also be tested with large datasets with more imbalance ratio. Similarly this framework can be tried on cost sensitive approaches and ensemble algorithms.
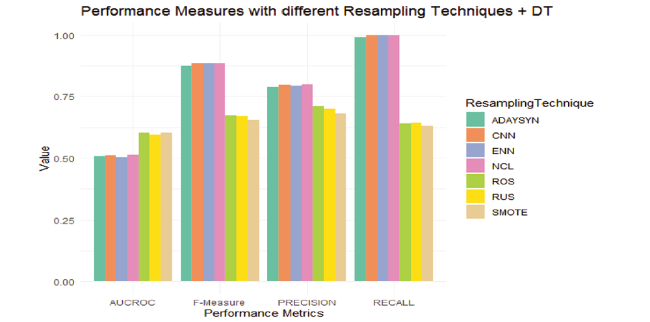
Figure 3. Comparative study of different sampling performances. |
Author contributions
K. Ulagapriya (ulagapriya@gmail.com) proposed the original idea,carried out the experiment and wrote the manuscript. S. Pushpa (pushpasangar96@gmail.com) analysed and reviewed the manuscript. Both authors discussed the results and contributed to the final manuscript.