1 Introduction
In the era of big scholarly data, scientific collaboration is becoming more and more prevalent due to the challenge of interdisciplinary research. The trend of increasing scientific collaboration has been confirmed in many studies (Barabási et al., 2002; Xia et al., 2017). Apart from that, scientific collaboration has been found to improve the quality of academic output, which plays a key role in the success of individual scholars and scientific teams (Lee & Bozeman, 2005; Kong et al., 2019). However, due to the rapid growth of academic data, it is increasingly difficult for scholars to find their needed information and potential partners from the massive academic data (Xia et al., 2017). So, to solve this problem, academic collaborator recommendation systems are designed to find potential collaborators for scholars (Liu, Xie, & Chen, 2018; Zhang et al., 2020). These recommendation systems aim to promote collaborative behavior in scientific research, improve the quality of the produced studies, and flourish the ecology of science and technology.
To help scholars find their potential collaborators, the design of the recommendation system focuses on how to measure the similarity among scholars. So far, various methods have been proposed to tackle this problem (Kong et al., 2017; Lopes et al., 2010; Xia et al., 2014; Zhou et al., 2021). The key of these methods is to quantify the relationships among scholars via various academic factors. Most of the design of the academic collaborator recommendation system considers different academic factors that may affect scientific collaboration, such as academic age (Wang et al., 2017), research interest (Kong et al., 2017), scholar influence (Zhou et al., 2021). Although many previous methods consider different aspects of scholarly attributes, it still cannot be a good supplement. In addition, these methods still have no good performance on large-scale networks. Recently, with the rapid development of network embedding technology, various embedding models have emerged. These methods learn the low-dimensional representation of nodes in large-scale networks, which performs well in link prediction (Aziz et al., 2020; Cen et al., 2019), node classification (Dong, Chawla, & Swami, 2017), and community detection (Chen et al., 2020).
In this paper, we propose an academic collaborator recommendation model based on attributed network embedding, which considers both the non-local structure of the academic collaboration network and multi-type scholar attributes. Specifically, we define non-local neighbors for capturing the strong relationships among scholars. Non-local neighbors can be obtained using a biased random walk and frequency filtering. At the same time, six different types of academic attributes are explored, namely, academic age, research interest, number of publications, average citations, number of collaborators and H-index. The long-distance dependencies in the network are further obtained by establishing attribute similarity. Ultimately, we use a semi-supervised deep model to preserve both the network structure and scholar attributes simultaneously. Overall, our contributions are mainly as follows:
•We propose an academic collaborator recommendation model which combines the network structure and multi-type scholar attributes.
•We define the non-local neighbors for scholars to capture strong relationships among scholars.
•We combine the multi-type scholar attributes to make up for the deficiency of considering only the network topology.
•We conduct extensive experiments with two real-world scholarly datasets, and empirically show that our proposed method performs better.
This paper is organized as follows. In section 2, we summarize the work related to our research problems. In section 3, we define our research problem. Then we present the details of our proposed model in section 4. Experimental results are reported in section 5. The conclusion and discussion are drawn in Section 6.
2 Related work
2.1 Academic collaborator recommendation
At present, the popular academic mining task is academic recommendation, which aims to help scholars deal with a large amount of scholarly data and find potential collaborators. Usually, the collaborator recommendation can be regarded as a problem of measuring the similarity among scholars. Approaches for recommending collaborator using similarity mainly include network structure-based, random walk-based, and deep learning methods. CN (Lü & Zhou, 2011) is a network structure-based approach, holding that the more scholars who have common neighbors, the more likely they will collaborate in the future. The method based on Random Walk with Restart (RWR) mainly uses random walk to capture the relationship among nodes. For example, Xia et al. (2014) explore three academic factors, i.e., coauthor order, latest collaboration time, and times of collaboration, to define link importance in academic social networks. Zhou et al. (2021) define the transition probability among different types of nodes via quantifying three academic relationships, i.e., researcher-researcher, researcher-article, and article-article. For recommending the most Beneficial Collaborator, Kong et al. (2017) studied researchers' topic distribution of research interest, interest variation with time, and researchers' impact in collaborators network.
Recently, some methods based on deep learning have been proposed. Liu, Xie, and Chen (2018) proposed a context-aware academic collector recommendation model CACR, which consists of the collaborative entity embedding network (CEE) and the hierarchical factorization model (HFM). CEE learns joint embeddings for researchers and topics with their mutual dependency. HFM exploits researchers' activeness and conservativeness to make high-quality new collaborator recommendations. Zhang et al. (2020) perform an improved random walk, generate specific node sequences capturing network structures, and then employ a novel graph recurrent neural framework to embed scholar attributes. ACNE (Wang et al., 2021) proposed by Wang et al., which extracts four types of scholar attributes based on the proposed scholar profiling model, can learn a low-dimensional representation of scholars considering both scholar attributes and network topology simultaneously. However, while many of the recommended models by academic collaborators take into account the fusion of network topology and scholarly attribute information, exploration of the highly nonlinear relationship between them is rarely studied.
2.2 Network embedding
In recent years, network embedding has flourished. The main idea of network embedding is to map the network into a low-dimensional latent space to maximize the preservation of network topological and node attributes information. In general, network embedding technology can be divided into two categories, topology network embedding, and attributed network embedding. Perozzi, Al-Rfou, and Skiena (2014) introduce word embedding into graph embedding. The proposed model DeepWalk adopts a truncated random walk to obtain the structural information of the network and uses the skip-gram model to learn the low-dimensional node embedding. The Node2vec (Grover & Leskovec, 2016) designed by Grover et al. proposes a biased random walk that can flexibly explore diverse neighborhoods. Wang, Cui, and Zhu (2016) utilize an auto-encoder to preserve the first order and second order proximity simultaneously. Most recently, some embedding methods enhance node representation by joining node attributes. To preserve the unique properties of each relationship while integrating information of different types of relationships, MNE (Zhang et al., 2018) represents it with high-dimensional public embedding and low-dimensional additional embedding. Cen et al. (2019) apply the multi-view network embedding approach to heterogeneous networks, which proposed a transductive and Inductive model to learn node embedding. Shi et al. (2019) adopt a meta-path based random walk strategy on heterogeneous information network embedding for the recommendation.
3 Problem definition
In this section, we first define some notations used in this paper, as shown in Table 1 . We then give some definitions and formulate the problem to be solved.
Table 1 Notations. |
| Notation | Description |
|---|---|
| G V E S A X Y d da $x_{i},\hat{x}_{i}$ $w^{(k)},\hat{w}^{(k)}$ $b^{(k)},\hat{b}^{(k)}$ | The attributed academic collaboration network The set of all scholars The set of relationship between scholars The weight of edge Scholar attribute matrix Adjacency matrix of multi-relational networks Final scholar embedding matrix Scholar embedding dimension Scholar attribute embedding dimension The input data and reconstructed data The k-th layer weight matrix The k-th layer biases |
Definition 1 (Academic Collaborator Recommendation): Academic social networks contain a wide variety of academic relationships among scholars. The goal of scholar collaborator recommendation is to help scholars tackle large-scale academic data and recommend the most suitable academic collaborators for them. We recommend potential collaborators mainly through the academic collaboration network structure features and scholar's multi-type attributes in this work.
Definition 2 (Attributed Network Embedding): Given a network G, it aims to learn a mapping function f : V → Y|V|×d, where d «|V| and |V| is the total number of nodes in the network. The objective of mapping function f is to map each node of G to a point in a low-dimensional latent feature space while preserving topology and attributes.
Based on the above definition, we can form our problem as follows. Given an academic collaboration network G, we aim at utilizing network structure and scholar attributes to learn low-dimensional scholar embedding. Finally, the obtained embeddings can help us explore potential academic collaboration relationships among scholars.
4 Methodology
In this paper, we introduce an Academic Network Embedding model for Collaborator Recommendation on Attributed network, called ACR-ANE. The model framework is shown in Fig. 1 . It mainly consists of three parts, preservation of non-local academic social network structure, preservation of attribute-based academic relationships, and learning scholar embedding based on deep neural network.
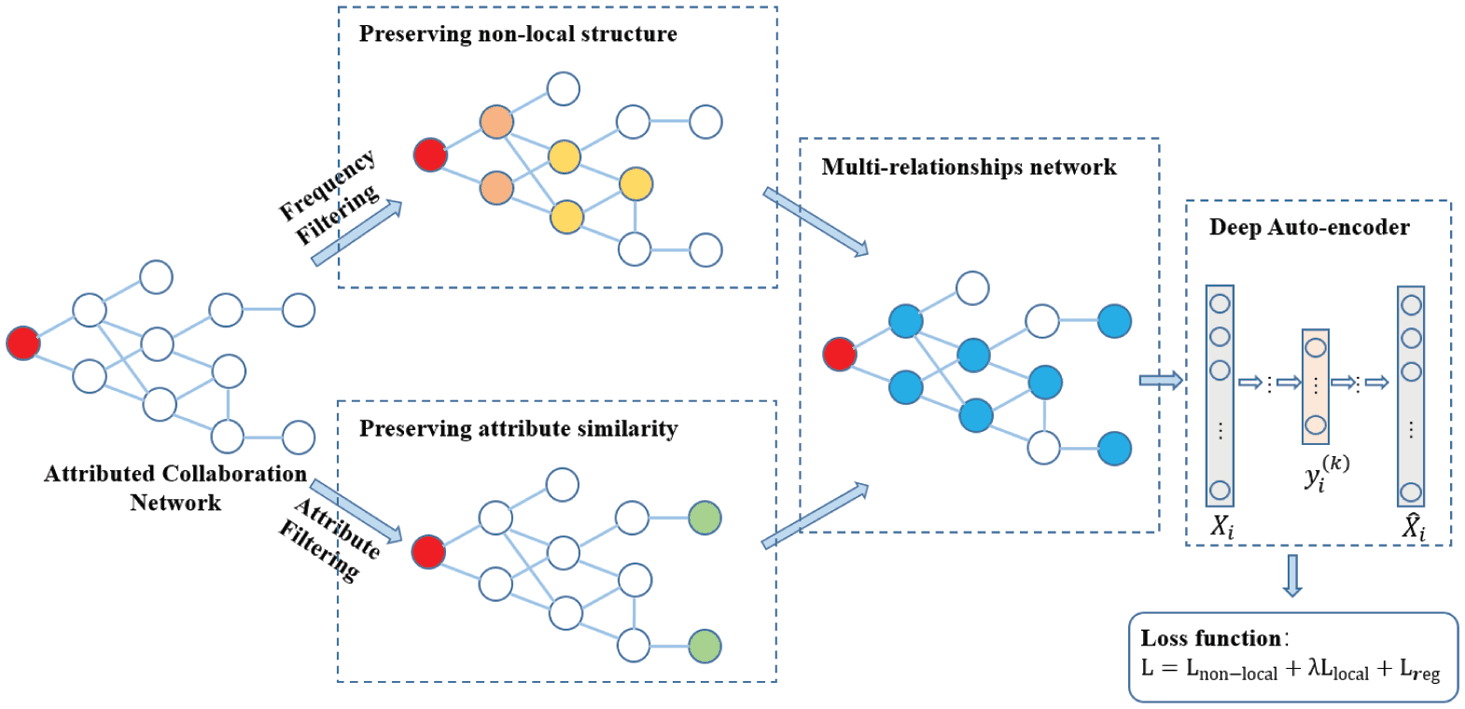
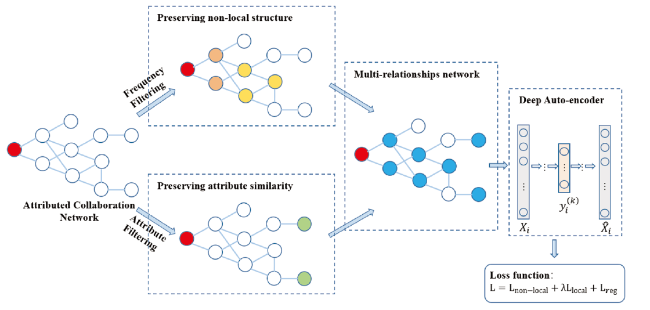
Figure 1. The framework of our proposed ACR-ANE model. |
4.1 Preservation of non-local academic social network structure
Usually, working with others is inevitable for scholars engaged in scientific research. Collaboration among scholars is now becoming more and more common. Studies have shown that collaboration will also promote the improvement of scientific output. Academic collaboration networks can help us discover academic social relationships among scholars. For example, the first-order neighbors of scholars in the network represent his co-authors. Describing relationships in networks with first-order neighbors proved efficient, but there are certain limitations in using it directly to mine academic relationships. In fact, for a specific scholar, scholars who have worked with him are not necessarily more likely to cooperate in the future than those who have never worked with him. That is, the relationships among scholars do not only depend on the near neighbors in the network. It also inspires us to reconsider the capture of academic network structure when predicting potential collaborators.
To more comprehensively capture non-local academic collaboration network structure, we define a new neighbor for each scholar, called non-local neighbors. Specifically, for each node in the academic collaboration network, the non-local neighbor comes from the nodes that start from the start node and passes through after T times of walk with a length of l. Note that our walk strategy builds on the Node2vec (Grover & Leskovec, 2016). After walking T times, we did not select the nodes of all the walk sequences. Here we set a filtering threshold Freq, to take partial nodes with their higher occurrence frequency as non-local neighbors of the start node. The reason for that is when we are building an academic collaboration network, the weight of links in the network is the number of collaborations among scholars. After a certain number of random walks and frequency filtering, the non-local neighbor nodes have a strong relationship with the start node.
Take an example, as shown in Fig. 2 . First, we select scholar a as the start node and set the number of walks as 5, and the walk length as 5. Under the guidance of link weight, we start the biased random walk from scholar a, after that, a series of scholars related to a will be sampled. Finally, based on the sampled nodes, after the operation of frequency filtering, we get scholar a's non-local neighbors b, c, e, f, h. It should be noted that among all the non-local neighbors of scholar a, even if some first-order neighbors are filtered out in the frequency filtering, their first-order neighbors should be involved.
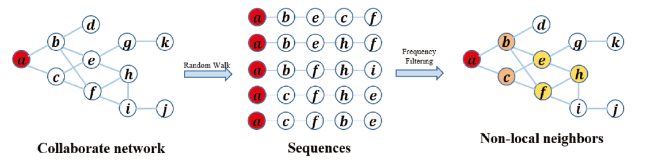
Figure 2. Capture non-local neighbors. |
4.2 Attributes information extraction for scholars
Recent studies have shown that it is necessary to consider the scholar's comprehensive attributes. However, although some recent works combine the scholar's attributes, they almost only consider one aspect, which is relatively not comprehensive for the grasp of the overall information of scholars. Therefore, for the recommendation of academic collaborators, it is natural for us to consider various attributes information of scholars. The following attributes for scholars are explored:
•Academic Age (AA): Academic age can be represented by the interval between the first paper and the last paper published by scholars within the period of our study.
AA = tcur - tfirst
where tcur is the year of the last paper published by the scholar up to the research point, and tfirst is the year of the first paper published by the scholar in the research period.
•Research Interest (RI): Many digital libraries provide abundant academic data, which makes it easy for us to access the historical publications of each scholar. Then, based on the topic and abstract information in scholarly history publications, we can get their research topic distribution via topic model, e.g. LDA (Blei, Ng, & Jordan, 2001).
•Publications (Pub): Number of all papers published by the scholar.
•Average Citations (AC): The average number of citations of papers published by the scholar.
•Collaborators (Co): The total number of historical collaborators.
•H-index (H): H-index is an important reference index to evaluate the influence of scholars. It refers to that the h-index of scientist is h if h of her papers have at least h citations and each of the remaining papers have less than h citations.
4.3 Preserve scholar attributes information
For the six different attributes mentioned above, we integrate them through the concatenate operation. Scholar attributes matrix A can be obtained by concatenation operation concat() as shown in Eq. (1).
A = concat(AA, RI, PUB, AC, CO, H)
Based on the attribute matrix A, we can calculate the attribute similarity among scholars with a cosine function. For example, assuming that Ai and Aj are the attributes embedding of scholar i and scholar j, respectively. The calculation of attributes similarity between them is shown as follows:
$ \operatorname{Sim}\left(A_{i}, A_{j}\right)=\frac{A_{i} \cdot A_{j}}{\left|A_{i}\right|\left|A_{j}\right|}=\frac{\sum_{m}^{d_{a}}\left(A_{i, m} * A_{j, m}\right)}{\sqrt{\sum_{m=1}^{d_{a}} A_{i, m}^{2}} * \sqrt{\sum_{m=1}^{d_{a}} A_{j, m}^{2}}} $
After obtaining the attributes similarity among scholars, we establish relationships for all scholars with their Top-K attributes similar neighbors. Here, we take nodes with high attribute similarity as attr_sim neighbors. As shown in Fig. 3 , suppose we aim to find scholar a's attr_sim neighbors. First, we use Eq. (2) to calculate the similarity of the attributes between a and other scholars. Then, we find scholars k, j and a have higher attributes proximity when we set the number of attr_sim neighbors as 2. Therefore, scholars k, j serve as the attr_sim neighbors of a, which could preserve the intrinsic similarity among scholars.
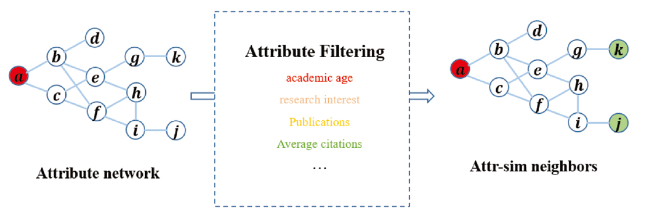
Figure 3. Capture attr_sim neighbors. |
4.4 Fusion of network topology and scholar attributes
The non-local neighbors and attr_sim neighbors describe the proximity of scholars on network topology and academic attributes levels, respectively. To integrate these two proximities, we construct a new multi-type relationship network for all scholars, combining their non-local neighbors and attr_sim neighbors, as shown in Fig. 4 . By integrating the two proximity, our multi-type relational network can also capture the similarity of attributes among scholars while preserving non-local network topology.
Figure 4. Preservation of multi-type academic relationships. |
4.5 Learning scholar embedding
To encode the academic collaboration network topology and scholar attributes into a low-dimensional representation space, we extend the traditional deep auto-encoders according to the literature (Salakhutdinov & Hinton, 2009). Deep auto-encoder is a deep neural network model for feature learning, which can learn highly non-linear topological and attribute features. It is an unsupervised model, consists of an encoder and a decoder. Formally, given the i-th row xi of the adjacency matrix X of multi-relational network, the hidden representations for each layer are shown as follows:
$ y_{i}^{(1)}=\sigma\left(W^{(1)} x_{i}+b^{(1)}\right) $
$ y_{i}^{(k)}=\sigma\left(W^{(k)} y_{i}^{(k-1)}+b^{(k)}\right), \quad k=2, \ldots, K $
where k is the number of layers for the encoder and decoder. $\sigma$() represents the non-linear activation function. W(k) and b(k) are the trainable parameters. Here, yi(k) is the final low-dimensional representation of the i-th scholar. After obtaining yi(k), we can get the output $\hat{x}_{i}$ by reversing the calculation process of encoder. The learning process can be simply described as minimizing the difference between the input xi and the reconstructed data $\hat{x}_{i}$. Therefore, we minimize the reconstruction loss LNon-local as follows:
$ L_{\text {Non-local }}=\sum_{i=1}^{|V|}\left\|\hat{x}_{i}-x_{i}\right\|_{2}^{2} $
In addition, we should also consider the importance of local network structure. That is to say, for the scholars who have collaborated, we hope that their representation will be closer, simultaneously. Here, the supervised loss LLocal for this goal is designed as follows:
$ L_{\text {local }}=\sum_{i, j=1}^{|V|} S_{i, j}\left\|y_{i}-y_{j}\right\|_{2}^{2} $
where Si, j ∈ {0,1}, which indicates whether there is a link between the node i and j. Finally, to preserve the global and local structure of the network simultaneously, we propose a semi-supervised model ACR-ANE based on deep auto-encoder, which combines Eq. (5) and Eq. (6) and joint minimizes the following objective function:
$ L=L_{\text {Non-local }}+\lambda L_{\text {Local }}+L_{\text {Reg }}=\sum_{i=1}^{|V|}\left\|\hat{x}_{i}-x_{i}\right\|_{2}^{2}+\lambda \sum_{i, j=1}^{|V|} S_{i, j}\left\|y_{i}-y_{j}\right\|_{2}^{2}+\frac{1}{2} \sum_{i=1}^{|K|}\left(\left\|_{W}^{(k)}\right\|_{2}^{2}++\left\|\hat{W}^{(k)}\right\|_{2}^{2}\right) $
Specifically, l is a linear trade-off parameter that adjusts the penalty between LNon-local and LLocal. LReg is an L2-norm regularizer term to prevent overfitting.
5 Experiments
In this section, we present the experiments of the proposed model ACR-ANE on two scholarly datasets, where the initial three sections present the experimental dataset, evaluation metrics, and Baseline methods. Then the experimental results and discussions are described in a further section.
5.1 Datasets
To evaluate the performance of ACR-ANE, we conduct experiments using two real-world scholarly datasets, including Aminer①(① https://www.aminer.cn/) and APS②(② https://journals.aps.org/datasets). The subset of Aminer dataset we extracted comes from the scientific publication information at the SIGMOD conference, ranging from 2006 to 2016. Then we extracted the top 100 scholars with the most published papers as seed scholars from the subset and extracted their collaborators from the entire network. After data processing, we obtain 7,436 scholars and 11,568 collaborative relationships. In addition, collaboration relationships of the 100 scholars from 2017 to 2019 are extracted to evaluate the performance of our model. Similarly, we use a subset of APS dataset with the journals of Physic Review A, B, and C for the experiments. After performing name disambiguation (Sinatra et al., 2016), we obtaind 5,102 scholars and 39,333 collaborative relationships from APS. Then we divided the datasets into two parts, including the training set with t = [2003, 2007] and the testing set with t = [2008, 2010]. The statistics of the datasets are described in Table 2 .
Table 2 Statistics of two datasets. |
| Datasets | # of Nodes | # of Links |
|---|---|---|
| Aminer | 7,436 | 11,568 |
| APS | 5,102 | 39,333 |
5.2 Evaluation metrics
We adopt three widely used metrics to evaluate the proposed recommendation model ACR-ANE, including Precision@k, Recall@k, and F1@k. Precision@k is a metric for indicating the proportion of new scholars in the recommendation list who have collaborated with the target scholars, defined as:
$Precision@k=\frac{Number of correct recommended collaborators}{Number of recommended scholars}$
And for Recall@k, which denotes the proportion of new collaborators recommended by the model who have actually collaborated with target scholars, defined as:
$Recall@k=\frac{Number of correct recommended collaborators}{Number of true collaborators}$
F1@k is an integrated metric of Precision@k and Recall@k, defined as:
$Fl@k=\frac{2*(Precision@k * Recall@k)}{Precision@k+Recall@k}$
5.3 Baseline methods
To evaluate the performance of the proposed recommendation model ACR-ANE, here we use the following baseline methods. For the rest baseline methods, their parameters are set following their original papers. A brief description of these methods is as follows:
•DeepWalk (Perozzi, Al-Rfou, & Skiena, 2014): DeepWalk is a classic deep learning model for network embedding. It uses a truncated random walk to obtain node sequence and then adopts Skip-gram model to train and generate scholars embedding. The gained scholar embedding can be used for similarity calculation for the recommendation.
•TADW (Yang et al., 2015): TADW based on matrix decomposition, which combines the topological structure and attributes features of collaboration network into scholar embedding.
•SDNE (Wang, Cui, & Zhu, 2016): SDNE adopts the auto-encoder and Laplace feature mapping to learn the scholar embedding. Notice that both DeepWalk and SDNE are plain network embedding approaches that do not consider any scholar attributes.
•ACNE (Wang et al., 2021): ACNE extracts four types of scholar attributes based on the scholar profiling model, which can learn a low-dimensional scholar embedding considering both scholar attributes and network topology simultaneously.
•ACR-NE: ACR-NE is a weakened version of ACR-ANE that only considers the network structure and does not incorporate scholar attributes in learning scholar embedding.
5.4 Results and discussions
In this part, we mainly study the impact of different experimental parameter settings, including scholar embedding dimension, scholar non-local neighbor filtering parameters. Finally, to demonstrate the effectiveness of the proposed method, we compare our model to the baseline models from three evaluation metrics.
5.4.1 Influence of non-local filtering parameter Freq
Freq indicates the filtering threshold when selecting the non-local neighbors. We analyze how the adjustment parameter Freq influences the performance of the proposed model on Precision, Recall, and F1. To obtain a better Freq, we conducted experiments on two datasets with 5 possible values for adjustment parameter, i.e. {10, 20, 30, 40, 50}.
The experimental results are shown in Fig. 5 and Fig. 6 , respectively. From Fig. 5 , we can observe that the model performance is gradually better when we increase the frequency from 10 to 30, while the Freq is greater than 30, the performance of the model shows a downward trend. Unlike Fig. 5 , Fig. 6 shows the performance of ACR-ANE on the APS dataset. From Fig. 6 (a)(b)(c), we can see that the model performs best when Freq is set to 10. Therefore, we set Freqas 30 and 10 for these two datasets, respectively. In addition, as shown in Fig. 5 (a) and Fig. 6 (a), we can see that the Precision shows an overall downward trend with the increasing value of recommendation list k. It is not hard to understand that as the recommendation list k increases, the probability that new collaborators of the target scholar will be recommended is greater. However, the increase in the number of new collaborators recommended is less than the increase in the recommendation list length k. Therefore, according to the definition of precision, we can see that precision decreases.
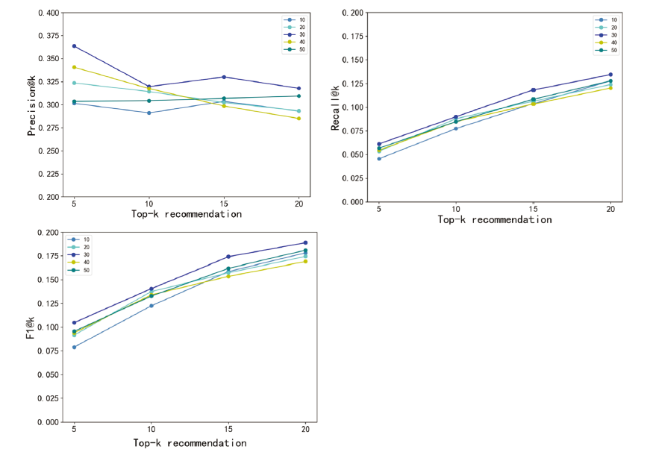
Figure 5. Influence of Freq on Precision, Recall, and F1(Aminer). |
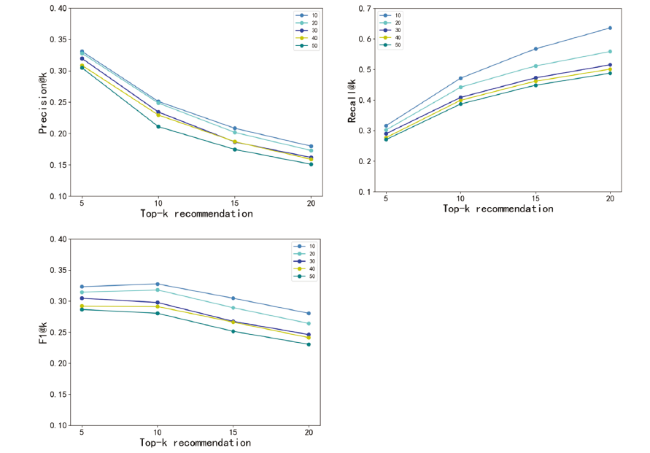
Figure 6. Influence of Freq on Precision, Recall and F1(APS). |
5.4.2 Influence of scholar embedding dimension
To obtain the ideal dimension of the embedding, we set the length k of the recommended list as 20, and the scholar embedding dimension is set as five different values, i.e. {40, 60, 80, 100, 120, 140}. We have conducted extensive experiments on AMiner and APS, and Precision@k, Recall@k, F1@k are used to evaluate the recommendation performance of the model under the different scholar embedding dimensions. What can be seen from Fig. 7 and Fig. 8 is that with the increase of scholar embedding dimension Dim, the overall performance of ACR-ANE is expected to increase accordingly, and then remain steady after a certain value. Specifically, the best performance of the model is achieved with a dimension of 120. Therefore, considering the above model performance, we set the scholar embedding dimension as 120 in the following experiments.
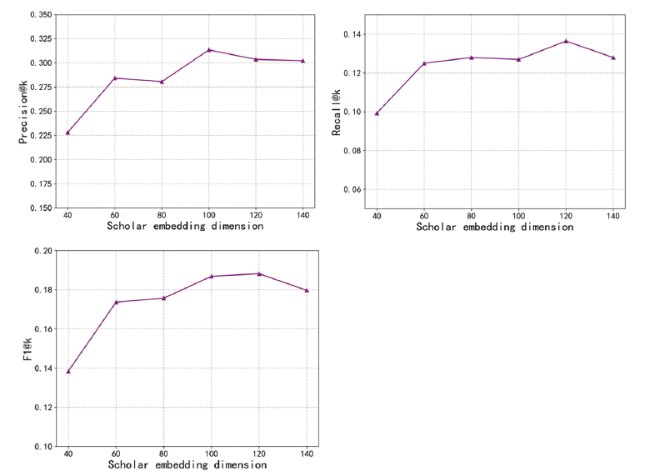
Figure 7. Influence of scholar embedding dimension on Precision, Recall, and F1(Aminer). |
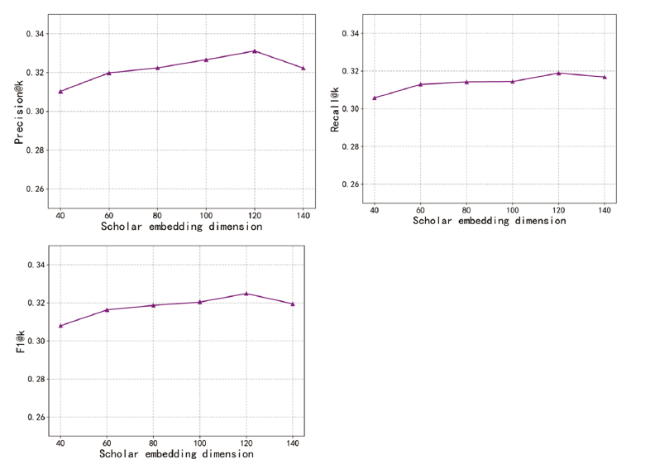
Figure 8. Influence of scholar embedding dimension on Precision, Recall, and F1(APS). |
5.4.3 Comparison with baselines
Our ultimate task is to recommend potential academic collaborators for scholars. In this section, we compare ACR-ANE with several baseline models. At the same time, to demonstrate the importance of scholar attributes information, we propose a variant of the ACR-ANE model, which is a weakened version that only considers the structure of the academic collaboration network and does not incorporate attributes in learning scholar embedding. Fig. 9 and Fig. 10 present the experimental comparison results on the Aminer dataset and APS datasets in terms of Precision, Recall, and F1. According to the experimental results, we can get the following observations:
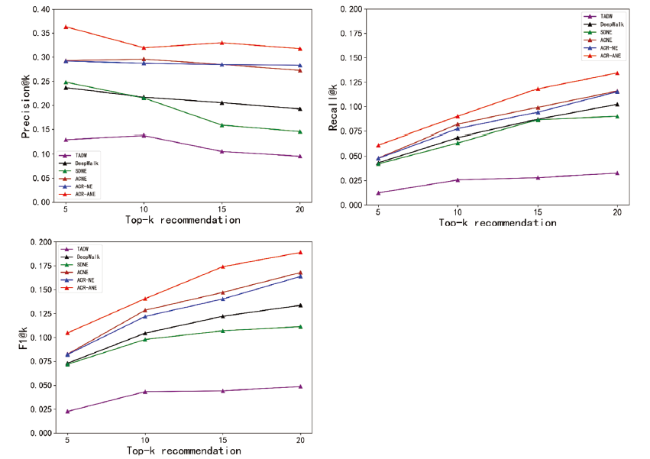
Figure 9. Comparison between ACR-ANE and baselines in terms of Precision, Recall, and F1(Aminer). |
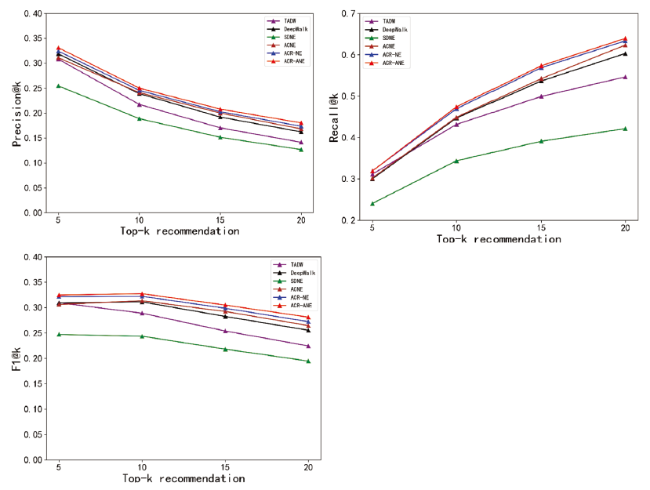
Figure 10. Comparison between ACR-ANE and baselines in terms of Precision, Recall, and F1(APS). |
1) Our proposed ACR-ANE has better performance in recommendation precision, recall, and f1 than all the state-of-the-art methods. This result shows the effectiveness of our proposed model in the task of academic collaborator recommendation.
2) While comparing with other network structure-based embedding models, ACR-NE performs best in the final recommendation task. It indicates the effectiveness of our proposed method to consider scholars' non-local neighbors in terms of capturing academic collaboration network structure. In contrast with ACNE, our proposed method performs better on two more datasets. Specifically, ACNE is an embedding model dominated by attribute information, while our proposed model is structure-dominated. The results demonstrate the importance of focusing on preserving the network structure for the final node representation learning.
3) Through the comparative analysis of ACR-ANE and ACR-NE, we can see that ACR-ANE performs better, which shows that it is significant to consider the structure of academic collaborate network and scholar attributes when recommending collaborators.
6 Conclusion
In this work, we propose an academic collaborator recommendation model for predicting potential collaborators of scholars. This model is designed based on network embedding, where the non-local network structure and the multi-type scholar attributes are jointly embedded via a deep auto-encoder. Specifically, to capture strong relationships among scholars, On the one hand, we use the biased random walk and frequency filtering to obtain their non-local neighbors. On the other hand, we extracted multi-types of academic attributes from the dataset to capture the similarity of attributes among scholars. And then the long-distance dependence in the network is further established via similar attributes. Finally, we conducted extensive experiments on two real-world scholarly datasets to evaluate the effectiveness of the proposed model. The results show that the proposed model ACR-ANE outperforms other state-of-the-art models in precision, recall, and F1. This paper deals with the static network, while the scientific collaboration network in the real world is dynamic. So, capturing the relationships among scholars based on the dynamic network will be our future work.
Acknowledgements
This work was supported by National Natural Science Foundation of China (No. 61603310) and the Fundamental Research Funds for the Central Universities (No. XDJK2018B019).
Author contributions
Ouxia Du (ou15881775735@163.com) proposed the original idea, carried out the experiment, and wrote the manuscript. Ya Li (crystal@swu.edu.cn) analyzed and reviewed the manuscript. Both authors discussed the results and contributed to the final manuscript.