This article brings together two independent strains of investigation. One is related to Mantel-Haenszel statistics (Agresti, 2019; Mantel & Haenszel, 1959; Smolinsky et al., 2022), and the other one is related to measures for collaboration intensity (Fuchs et al., 2021).

First, we recall the construction of the relative index of collaboration (RIC), a size-independent index (Fuchs et al., 2021). We investigate the meaning of this index, especially when it is close to one. Smolinsky et al. (2022) showed how to calculate the 95% confidence interval for indexes derived from contingency tables. We will show how the RIC can be derived from such contingency tables and hence how the method of Smolinsky et al. (2022) can be applied to it. Finally, we give an example of the use of such confidence intervals providing an interpretation of the calculated value of a RIC (here based on one database).

Analyzing the scientific collaboration between countries can be done by focusing on the authorship of publications as they are registered in a publication and citation database like the Web of Science (Clarivate Web of Science, 2022).

The vague term “collaboration” used above must be defined in more detail. In (Fuchs et al., 2021) the symbol C_XY denotes the number of publications under investigation written by at least one author of country X, at least one author of country Y, and possibly authors of other countries. These publications may be restricted by field or year of publication. When authors of two countries (based on their addresses) are co-authors in a publication we refer to this fact as a collaboration link between these two countries and to the publication as a collaborated publication. One publication can lead to at most one collaboration link between two given countries, even if three or more authors of these two countries are collaborating. We used whole counting, i.e., no fractionalization of any kind was applied. All of this leads to a collaboration network, with the countries X and Y as nodes of the network and C_XY as the weight of the edge between X and Y. For example, an additional paper with at least one author from the USA and one from Japan would raise the weight of the edge between the nodes USA and Japan by one unit.

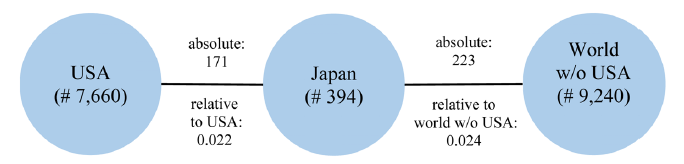
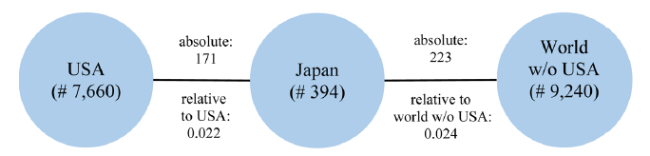
While the United Nations recognizes 193 sovereign states, the Web of Science also lists so-called regions, such as Wales or Taiwan. Hence, in many applications, it is not practical to draw a complete collaboration network (with more than 193 nodes and over 18,000 links). Therefore, focusing just on two countries we can simplify the graph and reduce it to three nodes (the two focal countries and the remaining part of the world) and the corresponding edges. Continuing the example of the USA and Japan, we consider the nodes USA, Japan, and all remaining countries registered in the WoS. To keep our example simple, we focus on the year 2020 and limit the publications to the WoS subject psychology (as we did in (Fuchs & Rousseau, 2021)). In this example, 171 publications had at least one co-author from Japan and at the same time at least one co-author from the USA. Hence, the weight of the Japan-USA edge is 171. We further had 394 publications with at least one author from Japan and one co-author from another country. This implies that 223 publications of these (394 minus 171) did not have any co-author from the USA. 7,660 publications had at least one author from the USA and at least one co-author from another country. 16,900 publications had at least two authors from two distinct countries, i.e., 9,240 publications of these (16,900 minus 7,660) did not have any co-author from the USA. We ignored 44,977 publications related to the year 2020 and the subject of psychology, because they were single-country/region publications, and did not contribute to the observed collaboration graph. For simplicity, we will refer to a publication in which at least two countries collaborate as a co-publication. Using the above-mentioned numbers, we derive the following representation (Fig. 1) summarizing all given information:

The collaboration between the USA and Japan (171 publications) seems to be not as intensive as the collaboration between Japan and the remaining countries (223 publications). This is not surprising as we are comparing a single country (the USA) against almost the whole world.

Consequently, we should not focus on the absolute number of collaborations to evaluate the intensity of collaboration between the USA and Japan, but on the relative intensity of collaboration. The probability of a collaborated publication by an author from the USA having a co-author from Japan is 2.2% (= 171 / 7,660), while the probability of a collaborated publication without an author from the USA having a co-author from Japan is 2.4% (= 223 / 9,240). Relating both probabilities to each other retrieves the Relative Intensity of Collaboration (RIC):

$\operatorname{RIC}(X, Y)=\left(\frac{C_{X Y}}{C_X}\right) /\left(\frac{C_Y-C_{X Y}}{T-C_X}\right)=\frac{C_{X Y} \cdot\left(T-C_X\right)}{C_X \cdot\left(C_Y-C_{X Y}\right)}$.

Here, C_X represents the number of collaborations of country X (i.e.,${{C}_{X}}=\sum\limits_{\left\{ Z|Z\ne X \right\}}{{{C}_{XZ}}}$, where Z is a country or region in the WoS database), C_Y represents the number of collaborations of country Y (i.e.,${{C}_{Y}}=\sum\limits_{\left\{ Z|Z\ne Y \right\}}{{{C}_{XY}}}$, Z as above), C_XY (= C_YX) represents the collaborations between these two countries and T stands for the collaborations of all countries (i.e.,$T=\frac{1}{2}\sum\limits_{\left\{ X,Y|Y\ne X \right\}}{{{C}_{XY}}}$. Applied to our example (with X=USA and Y=Japan), we get

This means that a publication by an author from the USA has not such a high probability to have a Japanese co-author as a publication without an author from the USA, or more specifically, a collaborated publication with an American (USA) author is only 92.5% as likely as one without an American author to have a Japanese coauthor.

The RIC indicator was introduced to correct the AOER-indicator by Luukkonen et al. (1992). It can be formulated in words as the ratio of the share of the collaborations of X and Y within all collaborations of X to the share of collaborations of Y (excluding those with X) within all collaborations of the system excluding all collaborations of X. We consider RIC to be better than AOER, among other reasons because if countries X and Y increase their collaboration while all other collaborations stay the same, then RIC(X,Y) increases, while this does not have to be the case for the AOER indicator. Note that RIC, as well as AOER, are asymmetric indicators because the relative collaboration importance of country Y for country X is usually not the same as the relative collaboration importance of country X for country Y. Indeed, one expects that, e.g., the importance of the USA for Mexico is much larger than the importance of Mexico for the USA. For a complete discussion of the difference between RIC and AOER, we refer the reader to (Fuchs et al., 2021; Rousseau, 2021). For another interpretation of the RIC indicator, we refer to (Fuchs & Rousseau, 2021). Recently, it has been shown how the RIC plays a role in the construction of a weighted Lorenz curve, used to characterize balance in collaboration (Rousseau et al., 2022).

Furthermore, we can quantify the intensity of collaboration as a correlation. Let o_USA be the odds of a collaborated publication of the Web of Science having an author from the USA. Then ${{o}_{USA}}=\left( \frac{7,660}{16,900} \right)/\left( 1-\frac{7,600}{16,900} \right)$. Let o_USA|Japan be the odds of a collaborated publication from an author from Japan having at least one co-author from the USA. Then ${{o}_{USA|Japan}}=\left( \frac{171}{394} \right)/\left( 1-\frac{171}{394} \right)$. Then RIC(USA,Japan) is exactly the coefficient, that transforms the first odds into the second, or in other words

It is of interest to know if the RIC value is above or below 1. Especially for RIC values near 1, quality attributes of the RIC are important, because our next examples show, that the statement RIC(USA,Japan) < 1 is not necessarily true for all publications, including those not mentioned in the WoS. We used WoS data to calculate this RIC value, but note that Heinze et al. (2019) showed that only about 70% of the psychology citations mentioned in the Web of Science refer to publications in this database. Putting it the other way around, about 30% or at least 18,000 publications are missing as referenced data. If we assume that the WoS-cited publications are of a similar quality as the WoS journal publications, then we can take the actual WoS journal publications as a sample of the larger sample space consisting of all WoS-indexed or cited articles.

This observation implies that the RIC of 0.925 we derived from the WoS does not have to be the real value (referring to all publications) of RIC(USA,Japan). Let us examine some extreme cases relating to the missing publications. Assume that all 18,000 missing publications are collaborations between the USA and other countries not being Japan.

Now, let us assume a second extreme scenario, where all 18,000 missing publications are collaborations only between Japan and the USA:

Other extreme cases would yield $RIC=\frac{171\cdot (9,240+18,000)}{7,660\cdot (223+18,000)}=0.033$ and $RIC=\frac{171\cdot (9,240+18,000)}{7,660\cdot 223}=2.727$.

Finally, if all missing publications are single-country publications, then, of course, RIC = 0.925.

We can conclude that the true RIC value has to be somewhere between 0.03 and 30.0. This is a very wide range and a more precise quality attribute of the RIC like a 95% confidential interval would be more informative. Assume that this interval would be [1.127] (this is in fact the 95% confidence interval as we will see later). Even though this is a more realistic range than [30.0] for the true value of RIC(USA,Japan) (i.e., the value of RIC if we would have the missing publications), we still have no evidence, if the true value of RIC is above or below 1. Consequently, we have to assume, that it is only a coincidence of our chosen set that the obtained RIC(USA,Japan) is below 1.

Smolinsky et al. (2022) elaborated on how to calculate the confidence interval of the RIC using contingency tables, see also (Katz et al. 1978). We find such tables everywhere, whenever the elements of a countable set can have two distinct attributes, i.e., the element e of a set E can possess the attribute X or not, and e can also possess the attribute Y or not. In general, we get a contingency table as shown below (Table 1):

Collaborations lead to such a contingency table, too. In this case, attribute X of a publication (i.e., the element e) is having an author from country X while attribute Y is having an author from country Y. This leads to Table 2.

The four upper-left parts shown in Table 2 (i.e., the table without the row sums and column sums) are completely disjoint in the sense that any publication under consideration (explicitly excluding single-country publications) contributes to exactly one of the four alternatives C_XY, C_X - C_XY, C_Y - C_XY, or T - C_X - C_Y + C_XY.

Table 2 corresponds to Table 3 cell by cell, where the variables a, b, c, and d are used instead. In the literature (like Smolinsky et al. (2022)), the notation with variables a to d is often used. Table 3 helps to transfer the results of common literature to our collaboration network and the RIC.

Table 3 alters the RIC to the formula $RIC(X,Y)=\frac{a/(a+b)}{c/(c+d)}$.

Before we finally look at the work of Smolinsky et al. (2022), we want to make a short excursion into biomedical statistics. This research field uses contingency tables for decades, where the attribute X is often the attribute if a patient has a disease (X) or not (not X). The attribute Y is associated with a positive test (Y) or a negative test (not Y) on this disease. The variables used in biomedical statistics are then a for true positive tests, b for false-negative tests, c for false-positive tests, and d for true negative tests. From such contingency tables, several indexes are derived. Just to recall some widely-used ones, we mention recall $\left( \frac{a}{a+b} \right)$, precision $\left( \frac{a}{a+c} \right)$, accuracy $\left( \frac{a+b}{a+b+c+d} \right)$, and the F-measure $\left( \frac{2a}{2a+b+c} \right)$. Also worth mentioning is the positive likelihood ratio $\left( \frac{a/(a+b)}{c/(c+d)} \right)$, which is equivalent to the RIC. Of course, these indices are also well-known in the field of information retrieval (Salton & McGill, 1983).

After this short excursion, let us now consider the results of Smolinsky et al. (2022). The authors start from data separated into K strata, where the data observed in each stratum can be summarized in a 2x2 contingency table like Table 3 only that Smolinsky uses the variables a_i, b_i, c_i, and d_i (i from 1 to K). In our application we only need one stratum (i.e. K = 1), hence we will just use our contingency Table 3 and do not mention strata anymore. Moreover, the original data related to the work of Smolinsky et al. (2022), namely those studied in (Bornmann & Haunschild, 2018), refer to articles published by a group, e.g., an institute, and their mentions in a social medium, such as Twitter. However, as long as contingency tables are following the meta schema we presented in Table 3, the different uses do not make any difference in the mathematical analyses of the various relations derived from these tables.

In their article (Smolinsky et al., 2022) the authors discuss the following three indicators (if restricted to one stratum): the row risk indicator RR^r, the column risk indicator RR^c and the odds ratio OR. Replacing their group G by country X and their group of mentioned publications by country Y, these three indicators referred to as formulae (1),(2),(3) in (Smolinsky et al., 2022) become:

Clearly, expressed in terms of collaboration, RR^r = RIC(X,Y) and RR^c = RIC(Y,X). The odds ratio does not play a role in our approach to collaboration relations.

As mentioned before, (Smolinsky et al., 2022) are using different strata, because every stratum is representing a special set of articles. The risk ratios (RR^c and RR^r) are derived for every stratum resulting in K different risk ratios and—by weighting these RRs—they are summed up to one single index, called the Mantel-Haenszel row risk ratio (MHRR) regarding RR^r and the Mantel-Haenszel column risk ratio (MHCR) regarding RR^c. Because we are observing only one single stratum, MHRR and MHCR are identical to their summands. Following equations (5) and (6) in (Smolinsky et al., 2022) we have:

Using the notation from (Smolinsky et al., 2022; p. 5, section 3.4) we retrieve the two coefficients:

Then, Var(ln(MHRR)) can be calculated by

and we obtain a 95% confidence interval related to ln (MHRR), which we transform by the exponential function e^x to a 95% confidence interval related to MHRR of the form

$\exp (\ln (MHRR)\pm 1.96\sqrt{VAR\left[ \ln (MHRR) \right]})$.

This confidence interval is the same as the confidence interval of the RIC, because of the relation MHRR = RIC. Returning to our example we get

In the next step, we calculate the 95% confidence interval of RIC(USA,JAPAN) by

In this investigation, we extended our investigations related to the Relative Intensity of Collaboration (RIC) indicator, by constructing confidence intervals for the obtained values. We followed the approach by Smolinsky et al. (2022) based on a new look at Mantel-Haenszel statistics. In this way, we combine the statistics of binary categorical data and bibliometric studies of collaboration. We note that this approach can be applied to any indicator derived from a contingency table.

We recall that bibliometric indicators are more often than not presented as “precise values” instead of an approximation depending on the database and the time of measurement. These precise values are descriptive statistics of the particular database and not of the entire literature. If they are interpreted as an indication of a broader set of literature, then they are being used as inferential statistics and confidence intervals give the computed values a basis for interpretation. Already forty years ago confidence intervals for the Journal Impact Factor were proposed by Schubert and Glänzel (1983), see also Nieuwenhuysen & Rousseau (1988) for a simplified approach.

We address four limitations, three of which are limitations on RIC but also common to bibliometric indicators. The fourth is common to confidence intervals derived from managed bibliometric databases.

1. When used with a classification in which journals or articles may have multiple classifications (e.g., Scopus, WoS), the RIC indicator for various fields will not be independent. For example, we examined RIC_Psychology which may have a significant correlation with RIC_Psychiatry. Of the 150 Psychology journals in the Journal Citation Reports of 2020, 83 are also classified as Psychiatry, so collaborations on articles in those 83 journals will contribute to both the 2020 RIC_Psychology and RIC_Psychiatry. Even when articles are assigned to a unique field a correlation would still remain because of the affinity between fields.

2. One can examine the RIC for the union of all fields, e.g., the entire WoS database ignoring field classification. This will give a measure of pairwise collaboration across all fields and an accurate measure of overall collaborative authorship activity. Nevertheless, some fields will be overwhelmed by the number of articles and collaborations in other fields and a subset of fields may dominate the result.

If one wishes to construct an indicator that is not a measure of simply overall collaborative activity, but includes a balance of all fields, then a stratified version of RIC may be necessary and is a possible area of further research.

3. Collaborations of a country can be counted in different ways as shown in (Fuchs & Rousseau, 2021). Two counting methods were discussed, one counting links between countries resulting in publications counted more than once if their authors were from more than two countries. The other counting method counted publications independent of the number of authors, resulting in alternative RIC values. Obviously, different counting methods represent different kinds of information.

4. A substantial limitation for obtaining confidence intervals for the RIC and any resulting comparison to the world is the sampling method. The choice of articles included in the database (e.g., WoS) is never completely objective, nor is it determined by researchers for the specific purpose they have in mind. One may consider the quality of WoS-cited articles and articles appearing in WoS-indexed journals equivalent, but, nevertheless, such citation indexes never constitute a random selection.

The authors thank the reviewers for their constructive comments.

Joel Emanuel Fuchs (joelemanuelfuchs@gmail.com): Formal analysis (Equal). Methodology (Equal). Writing—original draft (Equal). Writing—review & editing (Equal); Lawrence Smolinsky (smolinsky@math.lsu.edu): Conceptualization (Equal). Formal analysis (Equal). Investigation (Equal). Methodology (Equal). Writing—original draft (Equal). Writing—review & editing (Equal); Ronald Rousseau (Ronald.Rousseau@kuleuven.be): Conceptualization (Equal). Formal analysis (Equal). Investigation (Equal). Writing—original draft (Equal). Writing—review & editing (Equal).