1 Introduction
2 Assumption for causal inference using regression in observational studies
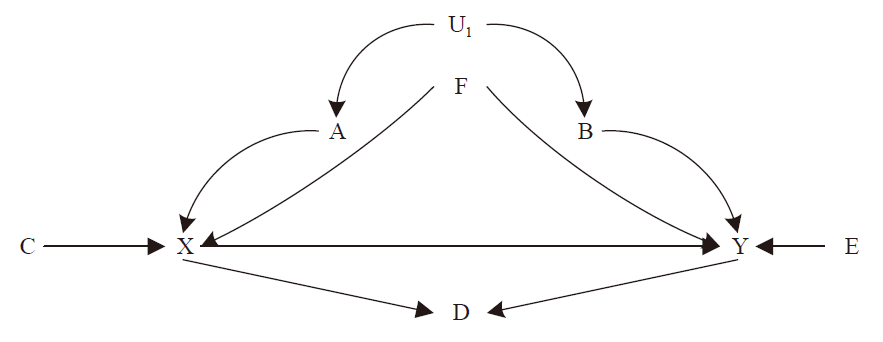
Figure 1. Causal diagram |

Journal of Data and Information Science >
Causal inference using regression-based statistical control: Confusion in Econometrics
Received date: 2022-10-24
Revised date: 2023-01-10
Accepted date: 2023-01-30
Online published: 2023-02-22
Regression is a widely used econometric tool in research. In observational studies, based on a number of assumptions, regression-based statistical control methods attempt to analyze the causation between treatment and outcome by adding control variables. However, this approach may not produce reliable estimates of causal effects. In addition to the shortcomings of the method, this lack of confidence is mainly related to ambiguous formulations in econometrics, such as the definition of selection bias, selection of core control variables, and method of testing for robustness. Within the framework of the causal models, we clarify the assumption of causal inference using regression-based statistical controls, as described in econometrics, and discuss how to select core control variables to satisfy this assumption and conduct robustness tests for regression estimates.
Key words: Causal Inference; Regression; Observational Studies; Econometrics; Causal Model
Fan Chao , Guang Yu . Causal inference using regression-based statistical control: Confusion in Econometrics[J]. Journal of Data and Information Science, 2023 , 8(1) : 21 -28 . DOI: 10.2478/jdis-2023-0006
Figure 1. Causal diagram |
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
/
| 〈 |
|
〉 |