1 Introduction
Recently, the availability of large-scale bibliometric datasets enables us better understand science, leading to the emergence of “science of science” field (Azoulay et al., 2018; Fortunato et al., 2018; D. Wang & Barabási, 2021; Zeng et al., 2017). As a prospect domain, the science of science deals with underlying regularities behind science, ranging from scientific careers (Liu et al., 2018; Zeng et al., 2019), to collaborations (Wu et al., 2019; Zeng et al., 2021, 2022), scientific impacts (D. Wang et al., 2013), and science funding (Azoulay et al., 2011; Y. Wang et al., 2019). Results emerging from the science of science have consequential effects on designing science policies. Take team science as an example, Wu et al. suggest that small teams tend to produce disruptive scientific papers, while large teams develop current knowledge (Wu et al., 2019). Moreover, prior studies confirm that scientific articles with diverse teams are more likely to be highly cited and novel (AlShebli et al., 2018; Yang et al., 2022). If teams with diverse memberships and small sizes tend to produce highly novel and disruptive research, how to design science policies to support such teams?
Generally, current studies in the science of science mainly use large-scale empirical datasets, including the Web of Science, the Microsoft Academic Graph, and Dimensions, among others. Researchers mainly focus on understanding correlational behaviors embedded in such datasets (AlShebli et al., 2018), or studying the underlying regularities in descriptive natures (Yin et al., 2022). Although recent research in the science of science uses causal analysis including Coarsened Exact Matching, Difference in Difference, and Regression Discontinuity Design, such methodology rooted in the field of economics seems not to attract much attention (Bol et al., 2018; Jin et al., 2021; Ma et al., 2020; Y. Wang et al., 2019). Yet, causal analysis is critical in designing science policies. For example, funders need to understand the causal impact of their investments, and simply comparing successful applicants with failed ones may lead to biased results. As it is often not feasible to run randomized experiments in social science studies, recent researches also use Regression Discontinuity Design to study the impact of scientific funding (Azoulay et al., 2019; Bol et al., 2018; Ganguli, 2017; Jacob & Lefgren, 2011b).
Among all causal inference methods, Regression Discontinuity Design (RDD) is one of the most credible quasi-experimental methods for identification, estimation, and inference of causal effects (Angrist & Pischke, 2009). RDD was first introduced by Thistlethwaite and Campbell in 1960 when they studied the effect of merit scholarship on students’ career development (Thistlethwaite & Campbell, 1960). Using the cutoff of the scholarship line, their results suggest that college aptitude tests increase the probability of obtaining a scholarship due to public recognition, but do not affect the students’ attitudes and career plans. The idea of using the cutoff to solve the problem of identifying ideal treatment and control groups has made RDD applicable to situations where rules have specific cutoff values, and individuals or units around the cutoff are assigned to the treatment and control groups randomly. RDD has been used in various studies since its introduction, and it has recently attracted much attention due to its transparency and potential applications to policy and program evaluations.
Recently, there has been a growing body of literature documenting the applications of RDD in various scientific domains, including labor economy, agricultural economy, environmental economy, public policy evaluation, education, and applied policy analysis, etc. (Anderson, 2014; Angrist & Pischke, 2009; Athey & Imbens, 2017; Ayres et al., 2019; Benavente et al., 2012; Bento et al., 2014; Bronzini & Iachini, 2014; Burger et al., 2014; Clark & Royer, 2013; Eibich, 2015; Ganguli, 2017; Hausman & Rapson, 2017; Henry et al., 2010; Huang & Zhou, 2013; G. W. Imbens & Lemieux, 2008; Jacob & Lefgren, 2002, 2011a, 2011b; Lang & Siler, 2013; Ludwig & Miller, 2007; Matsudaira, 2008; Moscoe et al., 2015; Thistlethwaite & Campbell, 1960). For example, Eibich estimated the effect of German retirement system on health conditions and behaviors, finding that retirement increases satisfaction in both physical and mental health (Eibich, 2015). Lalive et al. analyzed the joint retirement decisions of couples in Switzerland, finding that men and women are 28% and 12% less likely to be in the labor market around the full retirement age, respectively (Lalive & Parrotta, 2017). Recently, researchers have increasingly used RDD in environmental economics and agriculture to identify causal effects (Asher & Novosad, 2020; Ayres et al., 2019; Jones et al., 2022; Wuepper & Finger, 2022). In many real-world cases, various thresholds such as population level, poverty level, pay line, or farm size exist, making RDD a highly valuable tool in the empirical toolkit.
In this work, we provide a systematic survey of RDD, including its basic assumptions, mathematical notations, relationship with other scientific domains, and practical recommendations. Our survey aims to be comprehensive in terms of concepts and applications, but not in great technical detail. To better understand the history of the RDD, we also use bibliometric data to study the evolution of the RDD, providing a systematic view of the dynamic evolution of this field. Additionally, we employ the Web of Science and the Microsoft Academic Graph datasets to investigate the associations between RDD and other fields through citation analysis (Frank et al., 2019). Finally, we give practical recommendations using real-world datasets.
The rest of the paper is organized as follows. Section 2 introduces the basic assumptions of RDD. Section 3 discusses prior literature related to RDD and its applications, particularly the temporal evolution of RDD. In section 4, we provide explicit empirical recommendations on how to apply RDD in causal analysis.
2 Regression discontinuity design
In many real-world cases, it is challenging to estimate the causal effects of certain policy interventions without some initial plannings by administrators. For example, imagine that a science foundation wants to evaluate the impact of its funding program, and a group of awardees of that program published numerous scientific papers and trained many graduate students or postdocs ex post. It is not enough to conclude that this program has led to tremendous outputs. Rather, the funding agency needs to know what the awardees would have achieved had they not received such funding (Azoulay & Li, 2020). In the field of medicine, scientists perform randomized experiments to address such challenges by comparing outcomes for treated patients with outcomes for the control group, which are similar to the treated group but without any treatment. Such a strategy is also related to A/B testing in business settings. As a result, funding agencies that want to understand the real impacts of their funding programs need to compare successful scientists with failed ones who are identical.
Identifying failed scientists who are identical ex ante to the successful ones often requires randomized experiments in most cases. Thus, randomized controlled trials have become the gold standard for understanding treatment effects. In social science, however, such experiments are often not feasible due to ethical problems, and huge costs. In settings where random experiments are infeasible, RDD becomes a rigorous and flexible non-experimental method to learn about treatment effects of policy interventions. Consistent with prior work (Cattaneo & Titiunik, 2022), we use the potential outcomes framework to introduce RDD.
In an RDD setting, there must exist a cutoff, and the score and treatment assignment rule must be clearly defined in order to estimate the treatment effects. Specifically, suppose each individual has a score denoted by Xi, which is the running variable. Given that the cutoff denoted by c exists ex ante, individuals with Xi<c are assigned to the control group, i.e., Ti=0, while individuals with Xi≥c are assigned to the treatment group, i.e., Ti=1, where Ti represents the observed treatment status. Consequently, the observed treatment assignment is a function of the score for each individual. If all individuals assigned to treatment group actually receive treatment while individuals in control group remain untreated, we have P[Ti=1│Xi<c]=0 and P[Ti=1│Xi≥c]=1, which refers to the sharp RDD. On the other hand, fuzzy RDD refers to situations where P[Ti=1│Xi<c]≠0, P[Ti=1│Xi≥c]≠1, and there are significant differences between the treatment group and the control group near the cutoff. Thus, the treatment probability at the cutoff from zero to one is the key feature of the sharp RDD.
In the framework of potential outcomes, each individual has two potential outcomes, Yi(0) and Yi(1), where Yi(0) represents the outcome for individuals if they do not receive treatment, and Yi(1) represents the outcome if they do receive treatment. However, we cannot observe both outcomes for any individual in real-world cases. In order to estimate the treatment effect, we need to compare the average outcome levels of those who receive treatments and those who do not, which is expressed as E(Y(1)│T=1)−E(Y(0)│T=0). However, there are strong endogeneity issues to consider, as the observed treatment assignment Ti is often related to other observable and unobservable covariate variables. Let us revisit the funding evaluation problem. Simply comparing scientists who were supported by the program with those who were not is not enough, as awardees may have higher ability to produce scientific papers (or highly cited papers) than failed applicants in many aspects, thus they may publish substantially more papers, train more students, and win further awards.
To address this issue, Hahn et al. proposed that continuity around the cutoff score is the basic assumption of RDD (Hahn et al., 2001). Figure 1 a depicts the conditional expectation functions E(Yi(1)│Xi) and E(Yi(0)│Xi). Note that treated individuals cannot be observed when Xi<c, and individuals in the control group cannot be observed when Xi>c. Under the assumption of continuity, the conditional expectation functions E(Yi(1)|Xi=x] and E(Yi(0)|Xi=x] are continuous at the cutoff x=c,
$E\left[Y_{i}(1)-Y_{i}(0) \mid X=c\right]=\lim \limits_{x^{\uparrow} c} E\left[Y_{i} \mid X_{i}=x\right]-\lim \limits_{x \downarrow c} E\left[Y_{i} \mid X_{i}=x\right].$
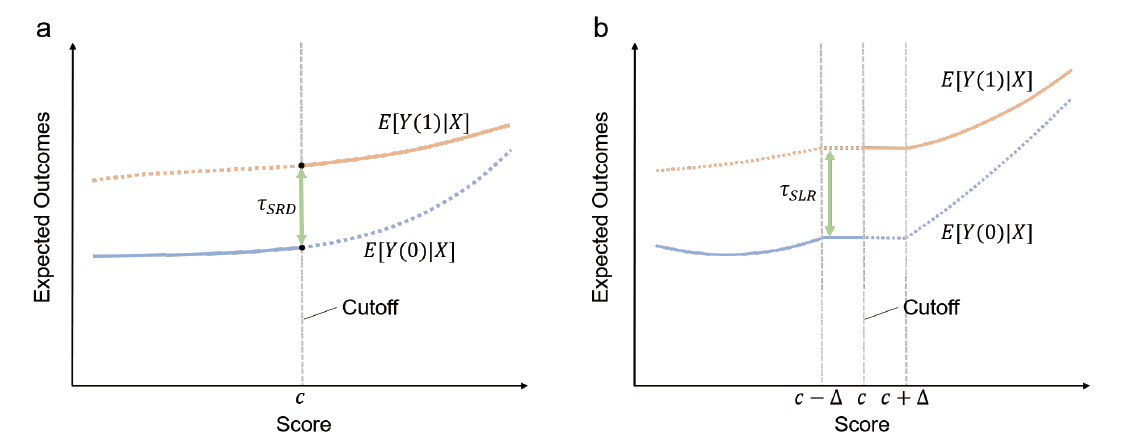
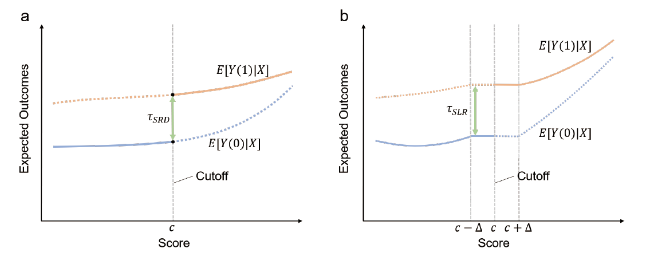
Figure 1. Illustrations of RDD. (a) The continuity framework, and (b) the local randomization framework. The figure depicts the expected outcomes conditional on the running variable Xi, denoted by E[Yi(1)|Xi=x] and E[Yi(0)|Xi=x]. τSRD and τSLR represent the causal effect using these two frameworks at the cutoff c in the window [c−Δ, c+Δ], respectively. This figure is adapted from (Cattaneo & Titiunik, 2022). |
In the sharp RDD, the average treatment effect τRD is captured only at the cutoff c, where x↑c represents the running variable approaches the cutoff c from the right, while x↓c the left,
τRD≡E[Yi(1)−Yi(0)|X=c].
Since Xi is continuous near the cutoff score c, we may conclude that these individuals receive the binary treatment assignment randomly near the cutoff. Namely, we can treat RDD near the cutoff as a local randomized experiment, which was introduced by Cattaneo et al. (Cattaneo et al., 2015). The key assumption of the local randomized trial is that individuals near the cutoff are randomly assigned to treatment (Cattaneo & Titiunik, 2022). It requires two conditions to fulfill this assumption. The first one is that the probability density function of the running variable X is continuous at the cutoff. The second condition is that the potential outcomes are not related to the score in the small window around the cutoff [c−Δ, c+Δ]. The local randomization approach rules out selection bias, and assumes that individuals in the treatment group and the control group are similar around the cutoff. To illustrate the local randomization approach, Figure 1 b shows that the treatment effect can be written as follows
τRD≡E[Yi(1)−Yi(0)|Xi=c]=Ew[Yi(1)]−Ew[Yi(0)],
where Ew represents the expected difference conditional on all Nω individuals in the small window around the cutoff. In the case of funding evaluation, one can compare scientific outcomes between awardees just above the funding pay line with failed scientists just below the pay line, and estimate the causal effect of funding on scientific outcomes using RDD.
If the treatment assignment and treatment receipt do not coincide for some individuals, we need to develop another approach, namely fuzzy RDD. Here, we introduce a variable Di, representing whether individual i received the treatment, i.e., Di=1 represents that the individual received the treatment. In settings of fuzzy RDD, some individuals with the running variable X smaller than the cutoff value c actually receive the treatment, and some individuals with X>c do not receive the treatment, and there is a significant difference in the probability of treatment at the cutoff
$P\left(D_{i}=1 \mid X_{i}\right)=\left\{\begin{array}{ll}g_{1}\left(x_{i}\right) & \text { if } x_{i} \geq c \\ g_{0}\left(x_{i}\right) & \text { if } x_{i}＜c\end{array}\right.$
where g1(xi)≠g0(xi). Note that g1 (xi) and g0(xi) differ at the cutoff value c. Thus, we can write the probability of receiving the treatment as
E(Di|xi)=P(Di=1|Xi)=g0 (xi)+[g1(xi)−g0(xi)]Ti,
where Ti=1 if xi≥c. In order to study the treatment effect, scholars focus on individuals in the narrow region around the cutoff c. The causal treatment effect in fuzzy RDD is
$\tau_{F R D}=\lim \limits_{\Delta \rightarrow 0} \frac{E\left[Y_{i} \mid c＜x_{i}＜c+\Delta\right]-E\left[Y_{i} \mid c-\Delta＜x_{i}＜c\right]}{E\left[D_{i} \mid c＜x_{i}＜c+\Delta\right]-E\left[D_{i} \mid c-\Delta＜x_{i}＜c\right]}$
Fuzzy RDD naturally leads to the instrumental variable framework, where Ti is the instrument variable. This approach assumes that the observed treatment assignment status Ti affects the outcome Yi through the treatment status Di only, i.e., Ti is uncorrelated with any observed or unobserved variables. In many cases, such a framework works fine if individuals or units cannot precisely manipulate the running variable X to be above or below the cutoff c. For example, scientists do not know precisely whether their proposal scores are above or below the pay line. Generally, scholars employ the two-stage least square (2SLS) regression to estimate the treatment effect (Aral & Nicolaides, 2017; Y. Wang et al., 2019).
In the first stage, one uses the running variable X to predict whether or not the individual will receive treatment:
Di=γ0+γ1xi+γ2xi2+…+γp xip+ρTi+ϵ1i,
where the probability to receive treatment can be described by pth-order polynomials, ρ is the first-stage effect of Ti on Di, and ϵ1i is the error term. In the second stage, one uses the predicted value of Di to predict the outcome variable Yi,
$Y_{i}=\alpha_{0}+\alpha_{1} x_{i}+\alpha_{2} x_{i}^{2}+\cdots+\alpha_{p} x_{i}^{p}+s \hat{D}_{i}+\epsilon_{2 i}$
where $\hat{D}_{i}$ is the predicted value of Di in the first stage and it is uncorrelated with ϵ1i, ϵ2i is the error term. In real cases, researchers often include control variables to ensure the robustness of the results. Alternatively, one can use the reduced form to assess whether a causal relationship exists, as follows:
Yi=α0+α1xi+α2xi2+…+αpxip+πTi+ϵ2i.
In practical cases, one can use the full sample with an appropriate value of p and all control variables, and then reduce the sample towards the cutoff c to eliminate all polynomial controls. It should be noted that the treatment effect estimated from the RDD applied to the local region around the cutoff c, and one cannot know whether such effect can be generalized to other regions far from the cutoff value.
3 The evolution of the regression discontinuity design
In this section, we provide a systematic study of the evolution of RDD, including the number of papers, citation patterns with other related fields, and its applications to other domains. Our sample is as follows: first, we obtain RDD papers from the Web of Science through keyword searches; second, we study citation patterns of RDD papers from the Microsoft Academic Graph (hereafter, MAG) (Sinha et al., 2015); third, we provide a survey on the application of RDD to other domains including science of science.
To study the evolution of RDD, we collect relevant papers from the Web of Science using keywords including regression discontinuity analysis, regression discontinuity, and regression discontinuity design. We manually check the data to eliminate articles that are irrelevant to RDD. Besides the first paper entitled “the Regression-discontinuity analysis: An alternative to the ex post facto experiment” published from 1960 to 2023, we obtain 3,387 RDD papers from the Web of Science (Figure 2 a). To study the citation patterns between RDD and other scientific domains, we match these papers with the MAG via paper DOIs (Sinha et al., 2015), resulting in 2,061 papers, 75,280 references pairs and 57,658 citations pairs from 1960 to 2021. We find that RDD papers showed a tremendous increase over time after 2010, especially in the field of economics and psychology, indicating that these two fields increasingly rely on RDD methods (Figure 2 b).
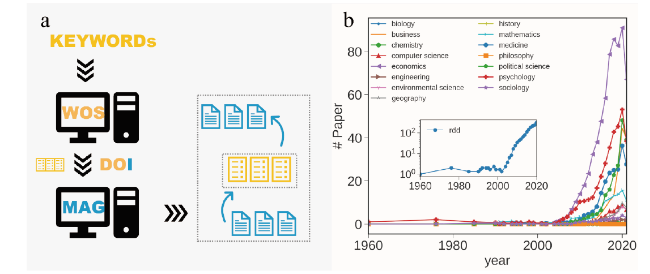
Figure 2. Data collection procedure. (a) Illustration of data collection procedure. Specifically, we manually collect 3,387 RDD papers from Web of Science through keyword searching, and we obtain 2,061 RDD papers in the MAG by matching their DOIs with the Web of Science data. (b) The number of RDD papers in 19 MAG categories as the function of time. The main plot is smoothed using a three-year sliding window. The inset figure shows the total number of RDD papers from 1960 to 2021. |
Since the first paper on RDD was published in 1960, the methodology was largely neglected for almost 30 years (Figure 2 b). During this time, RDD was not seen as substantially different from conventional causal inference methods such as matching, difference in difference, and instrumental variables. After 2000, interesting patterns emerged, with the field of economics leading the development of RDD. This observation suggests that scientists at that time focused on economics foundations of RDD (Figure 2 b), as evidenced by papers published by Angrist et al. (Angrist & Pischke, 2009), Hahn et al. (Hahn et al., 2001), Leuven et al. (Leuven et al., 2007), McCrary (McCrary, 2008), and Imbens et al. (G. Imbens & Kalyanaraman, 2012). Since 2010, many applications of RDD have been proposed in the field of economics and psychology.
To go beyond merely counting the number of publications, we also analyze the interactions between RDD and other academic fields through referencing and citation analysis. In particular, we investigate the share and strength of RDD papers in other fields, as shown below (Frank et al., 2019). The reference share from field A to field B is as follows:
share $_{t}(A, B)=\frac{\# \text { refs from A papers to B papers in year } t}{\# \text { refs made by A papers in year } t}$
which controls the total paper production of the referencing field over time. However, as papers in field B increased exponentially as a function of time, thus it may explain the evolution of the reference share measurement. We further normalize the reference share with the fraction of field B with respect to all papers, and define the reference strength as follows:
$\phi_{t}(A, B)=$ strength $_{t}(A, B)=\frac{(\text { refs share from A papers to B papers in year } t)}{\left(B^{\prime} s \text { share of all papers from } 1960 \text { to year } t\right)}$
Φt (A,B) > 1 indicates that referencing behaviors from field A to field B is greater than expected from random citation behaviors.
3.1 The global evolution of RDD papers
In this section, we will study the evolution of RDD over several decades. Specifically, we will present the results in two figures and one table. Figure 3 illustrates the development of RDD. We demonstrate citation patterns between RDD and other fields in Figure 4 . Table 1 shows the application of RDD in various research fields.
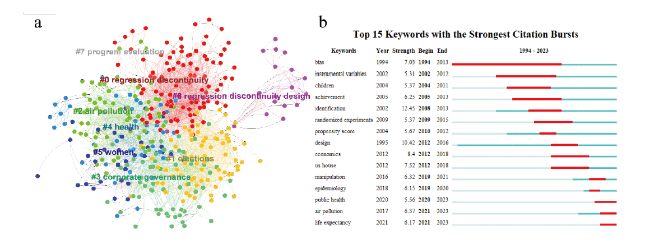
Figure 3. The RDD keyword network and emergent words in WOS. (a) We illustrate the RDD keyword network, where nodes represent keywords and links indicate that two keywords appear in the same paper. The modularity Q is 0.37, indicating a strong community structure. Here, we display only the largest eight clusters, excluding small clusters. (b) Top 15 emergent words of RDD papers, which indicate research frontiers. Year indicates the year when the keyword first appeared, while Begin and End represent the starting and ending years of the keyword as the research frontier. The graph on the rightmost displays the research frontiers in different time periods. For example, air pollution is the research frontier of RDD between 2021 and 2023. |
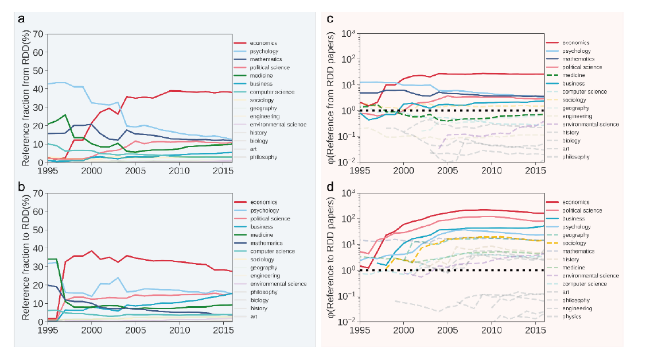
Figure 4. The citation behaviors between RDD and other academic domains over time. (a) The fraction of references made by RDD papers to certain scientific domains. (b) The fraction of references made to RDD papers by papers in various scientific domains. (c) Reference strength from RDD papers to papers in other academic fields. (d) Reference strength from other academic fields to RDD papers. Black dashed lines in c,d represent φ= 1, and other dashed lines in c, d indicate that the strength of references from certain academic fields is lower than the average value cross fields in 2016. |
Table 1. The survey of studies that utilize RDD. Context reveals the settings of the focal paper. Outcome(s) means the dependent variable of the focal paper. Treatment(s) is the treatment variable in the focal paper. In practice, the treatment variable is a binary variable. Running variable(s) is the forcing variable for individuals. |
| Context | Outcome(s) | Treatment(s) | Running Variable(s) | |
|---|---|---|---|---|
| Economics | ||||
| Yi et al. (Yi et al., 2022) | Great Famine in China | Risk tolerance and entrepreneurship in adulthood | Experiencing early-life hardship | Location |
| García-Jimeno et al. (García-Jimeno et al., 2022) | Women’s Temperance Crusade in American | Collective action decisions | Affective information networks | Location |
| Akhtari et al. (Akhtari et al., 2022) | The politically motivated replacement of personnel in the schools in Brazil | The quality of public education provision by the government | Political turnover | Share of Votes |
| Van Der Klaauw (Van Der Klaauw, 2002) | East Coast college’s aid | College enrollment | Offering financial aid | Aid allocation decisions |
| Education | ||||
| Davies et al. (Davies et al., 2018) | Reform of increasing the minimum school leaving age in England | Risk of diabetes and mortality | Remaining in school | Time |
| Huang et al. (Huang & Zhou, 2013) | Great Famine in China | Cognition estimated by episodic memory survey | Completion of primary school | Year of birth and entering primary schooling |
| Clark et al. (Clark & Royer, 2013) | Reform of increasing the minimum school leaving age in England | Adult mortality and health | Remaining in school | Time |
| Science of Science or Innovation Studies | ||||
| Seeber et al. (Seeber et al., 2019) | Scientists’ promotion in Italian higher Education system | Scientists’ number of self-citations | Undergoing the introduction of the habilitation procedure | Time |
| Wang et al. (Y. Wang et al., 2019) | Early-career setback, NIH R01 grant applications | Future Career outcomes | Receiving the R01 grant | Priority score |
| Bol et al. (Bol et al., 2018) | Innovation Research Incentives Scheme for early career scientists, Netherlands | Winning a midcareer grant | Winning the early career award | Evaluation scores |
| Bronzini et al. (Bronzini & Iachini, 2014) | Firms’ R&D subsidy in northern Italy | Investment spending of firms | Receiving funding | Priority score |
| Jacob et al. (Jacob & Lefgren, 2011b) | NIH R01 grant applications | Subsequent publications and citations | Receiving an NIH research grant | Priority score |
| Jacob et al. (Jacob & Lefgren, 2011a) | NIH postdoctoral training grants | Subsequent publications and citations | Receiving an NIH postdoctoral training grant | Priority score |
To present a holistic view of RDD, we first show its keyword network that consists of eight major clusters, named regression discontinuity, elections, air pollution, corporate governance, health, women, regression discontinuity design, and program evaluation (Figure 3 a). The nodes in the network represent keywords and the links indicate that the keywords appeared in the same paper. Specifically, the largest cluster contains keywords and papers related to regression discontinuity with an average publication year of 2014. The second largest cluster contains 96 nodes and is mainly related to election studies, with the smallest average publication year of 2004. This suggests that papers in political science studies applied RDD methodology to estimate the treatment effect.
When examining the evolution of RDD keywords, we observe interesting patterns that RDD research before 2002 was primarily centered on the development of RDD methodology, such as bias in 1994, design in 1995, and instrumental variables in 2002. However, after 2010, the development of RDD methodology allowed researchers to shift their focus to its application in various real-world scenarios, including the U.S. House election, public health, and environmental research on air pollution (Figure 3 b). In general, our findings suggest that RDD was initially driven by the development of methods and subsequently expanded to encompass various domains through its application.
Furthermore, we explore the knowledge spillovers of RDD to other scientific domains using MAG publication data from 1960 to 2021. The MAG identifies scientific fields of each paper using natural language processing methods, providing unique opportunities to study knowledge transfers (Frank et al., 2019; Sinha et al., 2015). We use citations between RDD papers and papers from other scientific domains to characterize their complex interactions. Such interactions indicate that the cited field reflects a piece of existing knowledge that the citing field builds upon (Sun & Latora, 2020). Specifically, we estimate the fraction of references made by RDD papers to papers from different scientific domains, finding that RDD papers often absorb knowledge from psychology, political science, and mathematics (Figure 4 a). We also track the fraction of references made to RDD papers from other domains over time, finding that economics, psychology, and political science show strong dependence on RDD, while medicine and business increasingly rely on RDD method (Figure 4 b).
Do the results change if we control for paper productivity? To this end, we estimate the reference strength from RDD papers to each academic field. Figure 4 c shows that RDD papers rely strongly on economics, and mathematics. Interestingly, although RDD papers increasingly cite medicine, such a pattern is balanced by the paper productivity of medicine (Figure 4 c). We find strong evidence that RDD method has been applied to various related domains, as most fields show higher than one reference strength to RDD papers (Figure 4 d). Specifically, economics, political science, business, and sociology strongly rely on RDD papers. Taken together, our systematic analysis shows that RDD exhibits strong applications in various scientific domains recently. There are strong interactions between RDD and mathematics in early years, suggesting math plays a fundamental role in forming the field of RDD.
Here, we present some cases regarding the application of RDD to other scientific domains. For example, research on the effects of education on individual development has emerged as a body of work. A recent study considers a British reform that increased the minimum school leaving age as a natural experiment. Using RDD, the authors find that remaining in school causally reduces the risk of diabetes and mortality (Davies et al., 2018). Other studies use similar approaches but find smaller effects (Clark & Royer, 2013). In political science, Akhtari et al. focus on the effect of political turnovers on the quality of public education (Akhtari et al., 2022). Using the sharp RDD, this study leverages closed elections (i.e., barely losing, and barely winning) as exogenous variations in political turnover, and finds that political turnover harms test scores for public schools due to the increase in the replacement rate. Using the fuzzy RDD, Garcia-Jimeno et al. make use of the highly nonlinear relationship between information networks and collective action decisions to study the effect of information flow on subsequent Temperance Crusade events (García-Jimeno et al., 2022). Moreover, prior research studies the effect of early-life hardship on adulthood entrepreneurship behaviors by leveraging China’s Great Famine as a natural experiment (Yi, Chu, & Png, 2022), as well as the effect of education on long-term cognitive reserve capacity (Huang & Zhou, 2013). Finally, a few other studies focus on the effects of financial aid offers on student enrollment decisions and student achievement (Henry et al., 2010; Van Der Klaauw, 2002).
3.2 The application of RDD to Science of Science
In this section, we focus on how RDD is applied to the science of science. Papers from science of science increasingly cite RDD papers, and researchers are interested in estimating the causal effects of policy interventions, such as government R&D expenditures (Bol et al., 2018; Jacob & Lefgren, 2011a, 2011b; Y. Wang et al., 2019).
Conventional science of science research mainly focuses on observable factors such as publications, individual scientists, or grants, making causal inference in science of science very challenging. Recent advances have presented an array of empirical research aimed at estimating the causal effect of a specific event (D. Wang & Barabási, 2021). A growing literature has shown the effectiveness of government expenditures in R&D for individual scientists, including scientific productivity and impact. Researchers use RDD to estimate the causal effect of funding by comparing outcomes of funded applicants just above the cutoff score with outcomes of failed applicants just below the cutoff based on evaluation scores (Bol et al., 2018; Y. Wang et al., 2019). For example, the success of an NIH R01 grant increases one additional scientific publication over the next five years (Jacob & Lefgren, 2011b). Similarly, Jacob et al. argue the positive effect of receipt of an NIH post-doctoral fellowship (F32 grant) on scientific productivity over the next five years, reflecting a 20% increase in scientific productivity (Jacob & Lefgren, 2011a). While the Matthew effect drives the allocation of science funding (Bol et al., 2018), a recent study using fuzzy RDD finds that near-miss applicants outperformed narrow-wins in the long run, consistent with the concept that “what doesn’t kill me makes me stronger” (Y. Wang et al., 2019). Seeber et al. study the extent to which scientists may strategically respond to bibliometric measures due to the introduction of a promotion regulation in Italy (Seeber et al., 2019). Using publication data of 886 scientists from four scientific domains, this study adopts RDD based on the nonlinearity of the relationship between the time trend and the number of self-citations. The authors find that the introduction of regulation had a strong and significant impact on self-citations for assistant or associate professors, who benefit the most from increasing citations. Moreover, Bronzini et al. evaluate a unique investment subsidy program implemented in northern Italy, finding no significant effects of the program on investment spending but a significant increase in investment for small enterprises (Bronzini & Iachini, 2014).
Overall, the application of RDD to the science of science is still limited, but the related literature is constantly growing over time. The main application is to evaluate the effects of scientific funding, policy interventions, or investment spending on various outcome variables such as scientific productivity, citation impact or scientists’ behaviors. As RDD requires a clear cutoff or threshold, we advocate that researchers need to find well-defined cutoffs or thresholds in science or related domains, contributing to the development of science of science and innovation.
3.3 Areas of research using RDD
In order to illustrate the applications of RDD, we summarize several studies that utilize the RDD in other domains. Table 1 includes the context of the study, the outcome variable, the treatment of interest, and the assignment variable. Note that the assignment variable determines whether individuals enter the treatment group, such as the admission score in education and review score in science funding.
4 Practical applications of RDD
This section describes the practical processes involved in implementing RDD, including identification, bandwidth selections, estimation, and some robustness tests (Moscoe et al., 2015). Furthermore, we provide a real-world case to estimate the impact of a government funding program. Note that we use the RD package developed by Cattaneo (Matias D. Cattaneo, 2021), which shows the RDD applications using Python, Stata, and R.
4.1 Identification
At the outset, researchers should determine whether sharp or fuzzy RDD is feasible for the data. Visualization is a simple yet powerful way to achieve this (G. W. Imbens & Lemieux, 2008). The first step is to see whether one can manipulate the running variable near the cutoff score. One should inspect whether there is a clear discontinuity in the distribution of the running variable x at the cutoff c. RDD relies on the local randomness assumption, so there must be a lack of prior knowledge of the cutoff. If there is no clear discontinuity in the distribution of the running variable, one should focus on the conditional mean of the outcome around the threshold c. A basic plot is straightforward but credible evidence for proving that the dependent variable has a discontinuity near the cutoff. More specifically, one can use the rdplot command in Stata as follows: rdplot y x, c(cutoff) p(n), where c(cutoff) represents the cutoff value as cutoff, and p(n) denotes the polynomial fitting (n=1 means linear regressions) (see Figure 5 a for a linear fitting plot). From Figure 5 a, we observe a possible discontinuity at the cutoff.
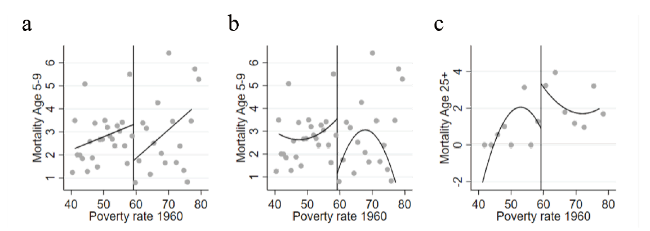
Figure 5. The results of the analysis conducted in (Ludwig & Miller, 2007). (a) - (b) show the linear and quadratic fits, respectively, using rdplot for county mortality of children aged 5 to 9 in 1973-1983. (c) shows the quadratic fit using rdplot for county mortality of people ages 25 and older in 1973-1983. The data used in the analysis come from (Matias D. Cattaneo, 2021). |
4.2 Estimation
As shown before, RDD has two frameworks, i.e., continuity and local randomization framework. The former estimates the effect using the full dataset and the latter estimates the effect using only the data near the cutoff. In practice, it may be best to estimate multiple specifications using both methods.
When using the full data, it is common to compare flexible models with higher order polynomial terms to linear models (Calonico et al., 2017). To do this, one can estimate parameters using ordinary least squares (OLS) and then select the optimal model. Specifically, different orders (usually smaller than 4) of the running variable X are generated, and the best model is chosen based on the minimum value of the Akaike Information Criterion (AIC) or Bayesian Information Criterion (BIC).
When using local polynomial regressions, selecting the bandwidth is the primary work, and there is a default bandwidth procedure available in the Stata command rdrobust. Specifically, one can use the following command:
rdrobust y x, c(cutoff) p(2)
This command uses local quadratic regressions and reports the treatment effect of outcome y. The cutoff score is specified as the cutoff, and its best bandwidth is estimated using the default method. Moreover, one can manually select the optimal bandwidth by using rdwselect y x, c(cutoff).
4.3 Robustness checks
One usually needs to perform a series of robustness checks when conducting RDD analysis (Cattaneo & Titiunik, 2022). The first test is to test whether the running variable is continuous near the cutoff score. One can plot the distribution of the running variable to see whether there is a discontinuity in the distribution near the cutoff score. Moreover, McCrary proposed a quantitative test for this purpose, i.e., the McCrary test (McCrary, 2008). The second test is to evaluate the sensitivity of the bandwidth selection. One should vary the bandwidth to see if the estimated results are robust. The third test is the cutoff score placebo test. Specifically, one can consider other scores as the hypothetical cutoff and use the same RDD method to estimate the causal effect. One should expect that the main effect disappears when using other cutoff scores. Finally, one should test the sensitivity of the samples by eliminating samples based on quantiles from the population.
4.4 A real-world case
In this section, we estimate the spillovers of fiscal funding, i.e., whether the government funding program improved children’s health. The Office of Economic Opportunity (hereafter, OEO) developed the Head Start funding program (hereafter, HS) in 1965 to provide health and other social services to children at ages 3 or 4 in poor counties in the US. Ludwig et al. (Ludwig & Miller, 2007) show that this program effectively reduces child mortality rate in the subsidized counties using RDD. Here we aim to reproduce their results to demonstrate the application of RDD in empirical research.
In this case, the OEO supported the 300 poorest counties according to the poverty rate in 1960, and the country with the lowest poverty rate among all counties in the US is 59.198%. This means that the running variable is the county poverty rate in 1960, and the cutoff score is 59.198%. We use the sharp RDD method to estimate the effect of the HS program on children’s mortality for counties that received the treatment, implied by:
Mc = m(Pc)+ αTc+νc
where c represents a county, and Mc, the outcome of interest, is the mortality rate of children aged 5 to 9 in 1973-1983, considering that children aged from 5 to 9 could have been involved in the HS program when they were 3 years old. m(Pc) is a smooth function of 1960 county poverty index. Tc is a binary variable equal to one if Pc≥ P300, zero otherwise. α is the impact of HS, and νc is the error term.
Specifically, we use county-level data that include the 1960 poverty rate for U.S. counties, the 1973-1983 child mortality rate for HS-eligible children aged 5-9, and the mortality rate for HS-eligible individuals aged 25 and above. As the HS program has a clear assignment rule based on the poverty rate, we estimate the effect of this program using samples around the cutoff. We conduct a kernel-weighted linear regression for both the left and right points of the OEO cutoff (i.e., 1960 county poverty 59.198%) separately, and estimate the treatment effect as the difference between the left and right limits of the regressions at the cutoff.
We display results for a broad range of candidate bandwidths. Table 2 presents the 1960 poverty rate, the mortality rate for children aged 5-9, and the mortality rate for young adults aged above 25 for counties with poverty rates 10% above and below the cutoff value. We find that the mortality rate for children aged 5-9 living in HS-eligible counties shows clearly smaller values, whereas the mortality rate for individuals aged above 25 shows limited differences. Table 3 shows the regression discontinuity estimation regarding the effect of the HS funding program on mortality. Our findings indicate that the HS funding led to a significant decrease in mortality rates for children aged 5-9 in 1973-1983 (Figure 5 a b, Table 3 ). Furthermore, we confirm the effect by finding no statistical difference in mortality for people aged 25 and older (Figure 5 c Table 3 ).
Table 2. Counties Characteristic. Column 1 represents county-level data, including the county poverty rate in 1960, mortality of children aged 5 to 9, and people aged 25 and older in 1973-1983. Counties with a 1960 poverty rate of 49.198% to 59.198% are the control group, while counties with a 1960 poverty rate of 59.1984% to 69.1984% are the treatment group, i.e., the poorest counties funded by the HS funding program. |
| County-level data | Counties with 1960 poverty 49.198% to 59.198 | Counties with 1960 poverty 59.1984% to 69.1984 | ||
|---|---|---|---|---|
| No. of observations (counties) | 347 | 228 | ||
| Mean | Std | Mean | Std. | |
| County Poverty Rate 1960 (%) | 54.08 | 2.861 | 63.40 | 2.644 |
| Mortality, Ages 5-9, 1973-1983 (%) | 3.044 | 5.897 | 2.316 | 4.566 |
| Mortality, Ages 25+, 1973-1983 (%) | 132.5 | 30.96 | 135.7 | 30.53 |
Table 3. Regression discontinuity estimation of the effect of HS funding on mortality. Robust standard errors are in parentheses，*** p<0.01, ** p<0.05, * p<0.1. |
| (1) | (2) | (3) | (4) | (5) | ||
|---|---|---|---|---|---|---|
| Parametric | ||||||
| Variable | Mean | Nonparametric estimator | Flexible linear | Flexible quadratic | ||
| Bandwidth or poverty range | 9 | 18 | 36 | 8 | 16 | |
| Main results | ||||||
| Number of countries | 524 | 954 | 2,161 | 482 | 858 | |
| Mortality, Ages 5-9 (%) | 2.252 | -1.895* | -1.198* | -1.114** | -2.201** | -2.558** |
| (0.984) | (0.662) | (0.501) | (1.058) | (1.096) | ||
| Mortality, Ages 25+(%) | 132.626 | 2.204 | 6.016 | 5.872 | 2.091 | 2.574 |
| (5.645) | (4.025) | (3.600) | (5.872) | (6.370) | ||
5 Discussion
As the science of science is of interest to policymakers, it is critical to use causal inference methods in this emerging field to design effective science policies that can support and nurture junior scientists or innovative teams. In this work, we provide a systematic survey of RDD, and demonstrate how to use this method to estimate causal effects. We provide detailed descriptions of its key assumptions as well as mathematical notations. Moreover, we examine the evolution of RDD and its citation patterns with respect to other scientific domains. In the case study, we apply the RDD method and find that the Head Start funding program significantly reduces child mortality rates for children aged 5 to 9. As RDD is a powerful tool for program or policy evaluations, we advocate that researchers in the science of science field should take notice of this method. More importantly, funders, universities, or other related agencies should also be aware of this method to better evaluate their programs.
Since the ground-breaking work by Thistlethwaite and Campbell, current RDD works offer abundant concrete and theoretical implementations from various scientific domains. We find that scientists typically developed RDD methodologies before 2000, which rely heavily on economics and mathematics. After 2008, RDD methods have been widely applied to various domains. Our results also suggest that RDD is a highly valuable tool in the field of science of science and its potential applications have not been fully exploited yet.
As a prominent area in science of science, estimating the impact of funding has attracted numerous attention. Many researchers from science of science, sociology of science, as well as innovation fields have provided valuable insights into this question. However, many studies rely on data from the National Institutes of Health (Azoulay et al., 2019). Funding data, especially for other countries, are quite limited, which prohibits researchers from evaluating the impact of funding. In addition to funding data, there are many contexts in science that involve cutoffs. For example, many valuable papers were rejected initially, and studying the impact of such events on the development of individual careers has policy implications for nurturing junior scientists (Calcagno et al., 2012).
Finally, we present a checklist for using RDD in the field of science of science.
• First, test whether there might be a manipulation of the treatment assignment variable. This can be done by presenting a histogram of the running variable using different numbers of bins. Quantitative tests such as the McCrary test can also be used to test for a discontinuity of the running variable around the cutoff score.
• Second, present the main RDD plot using local averages or polynomial fitting methods. Software such as Stata or R has typical toolboxes to achieve this.
• Third, explore the sensitivity of the results by varying the bandwidth or the order of polynomial fittings. Estimate the discontinuity of the outcome near the cutoff using both nonparametric and parametric estimations.
• Finally, add some controls to see whether the results are robust. Additionally, one may change the cutoff value in order to conduct placebo tests.
Lastly, the fuzzy RDD can be simply conducted using the conventional 2SLS method.
Acknowledgments
We thank Ludwig et al. and Cattaneo et al. for the HS dataset.
Author contributions
Meiling Li (21mlli@stu.xjtu.edu.cn): Methodology; Software; Formal analysis; Writing original draft. Yang Zhang (zhangyang_xjtu@163.com): Methodology; Formal analysis; Writing original draft. Yang Wang (yang.wang@xjtu.edu.cn): Conceptualization; Supervision; Project administration; Writing review & editing.
Conflict of interest statement
The authors have no competing interests.
Funding information
This work was supported by grants from the National Natural Science Foundation of China under Grant Nos. 72004177 and L1924078.
Data availability
We downloaded RDD papers from the Web of Science, the MAG dataset is publicly available, and HS data was downloaded from https://rdpackages.github.io/.