1 Introduction
Collaboration has become a common practice in scientific production (Hara et al., 2003; Hu et al., 2020; Newman, 2004; Regalado, 1995). While scientific collaboration promotes publication output and the work’s impact (Dong et al., 2017; Pravdić et al., 1986; Wu et al., 2019), it brings difficulties in determining who gets how much credit for the team’s work (Hodge et al., 1981; Zeng et al., 2017). This gives rise to a new problem of credit allocation, which aims to quantitatively calculate the share of the credit by each author (Allen et al., 2014; Kennedy, 2003). However, as most important decisions in science, such as job appointment, funding application, tenure promotion, and award nomination, are based on the achievements of the individual (Jones, 2011), it is more important for credit allocation methods to accurately and confidently identify the leading author or the owner of a collaborated work (Rennie et al., 1994; Smolinsky et al., 2020), the one who gets the most credit among all authors.
In practice, the science community has developed several ways to solve the credit allocation problem. One is to consider all co-authors in the team get the same credit for the work (Burrell et al., 1995; Oppenheim, 1998; Price, 1981; Rennie et al., 1994). Equivalently, any co-author can claim himself/herself as the owner of the work. This is most common in fields like Mathematics, Economics, and Particle Physics, where the author’s name is usually listed alphabetically in the paper (Endersby, 1996; Frandsen et al., 2010; Waltman, 2012).
The other way takes the byline order of authors into consideration (Beveridge et al., 2007; Riesenberg et al., 1990; Zuckerman, 1968). The last author, who is usually the corresponding author, and the first author take a greater share of the credit. Considering the observation that the first and last authors usually conduct most jobs of the work (Tscharntke et al., 2007), it seems fair to make them the owner of the paper. While these two approaches have their pros and cons (Das et al., 2020; J. Xu et al., 2016), they are widely applied in the science community for their simplicity and feasibility.
Recently, an algorithm-based approach is proposed that tackles the credit allocation problem from a new angle (Shen & Barabási, 2014). The leading author of a paper is not determined by factors on that paper, such as the byline order of authors, but is determined by the perception of the scientific community. By analyzing how the target paper and papers by the team members are co-cited, the leading author can be quantitatively identified, who is the one most appreciated by peers in the community and recognized as the leader of the teamwork. The original method and other variants (Bao et al., 2017; F. H. Wang et al., 2019; J. P. Wang et al., 2019; Xing et al., 2021) are tested in empirical data and demonstrate high accuracy in determining Nobel Prize laureates from the team that uncovers the scientific discover together.
However, existing methods present several limitations that can be further addressed. First, it is important to determine the weights of different papers in the citation network (H. Huang et al., 2022; Waltman et al., 2013). the number of citations, which has been widely accepted as a measure of a paper’s awareness (Eysenbach, 2006; L. L. Xu et al., 2021; Waltman, 2016; Radicchi et al., 2008; Sinatra et al., 2016), is considered by some methods and improves their performance. But given the scale-free nature of the citation distribution (Barabási, 2009; Barabási et al., 2001; Barabási et al., 2003), the weights of papers can be very screwed towards some highly cited ones. Second, the robustness of the method needs to be further verified and strengthened. As one can publish papers that intentionally cite the target paper and ignore other related co-publications, the methods have to be robust to such manipulations. Finally, to identify the leading author of the paper, we would prefer that the best candidate is distinguishable from others. If the methods give close or tied scores to candidates in the first and second positions, the leading author may be indistinguishable. This issue can be critical in dealing with large-scale data. For instance, if one wants to investigate the correlation between the leading author of a paper and his/her byline order in the author list (Lu et al., 2022), the method has to ensure that the identified owner of a paper is well separated from other co-authors.
To address the aforementioned issues, we propose a new allocation algorithm called NCCAS. We use a modified Sigmoid function that transfers citation counts to weights of different papers, which successfully solved the issue of the fat-tail distributed citation numbers. Furthermore, we remove the target paper in the credit calculation, which brings improved distinguishability of the identified leading author. Following the testing framework of previous studies, we validate the accuracy of NCCAS using Nobel Prize-winning papers and their citation networks in the American Physical Society (APS) and the Microsoft Academic Graph (MAG) dataset. In addition, we use 654,148 articles published in the field of computer science from 2000 to 2009 in the MAG dataset to validate the distinguishability and robustness of NCCAS. Compared with other baseline methods, NCCAS not only identifies Nobel laureates in their collaborated papers more accurately, but also assigns higher scores to them, making the leading author of the work more distinguishable from other candidates. In addition, NCCAS is more robust against additional citations in hypothetical malicious manipulation experiments. Given NCCAS’s capability in handling large-scale publication data and its nice performance, it has the potential to be a useful tool in other studies related to different roles or contributions of authors.
2 Related work
The first collective credit allocation (CCA) algorithm is introduced by Shen and Barabási (2014). As shown in Figure 1 , assume a target paper p0 co-authored by author A and author B. To identify which author is recognized more by the community, we need to identify all papers that cite the target paper. Through the set of citing papers, we further identify the set of papers that are co-cited with the target paper and are co-authored by at least one of the two authors. From the set of co-cited papers, we get an authorship involvement matrix A that counts the fractional share of authorship of the two authors in each co-cited paper. Furthermore, we get a strength vector s that assigns different weights to co-cited papers. In CCA, the element of s is the number of co-citations one co-cited paper receives with the target paper. The product of the matrix A and the vector s gives the total score of authors A and B, which represents the overall appearance of each author in related co-cited literatures weighted by their importance.
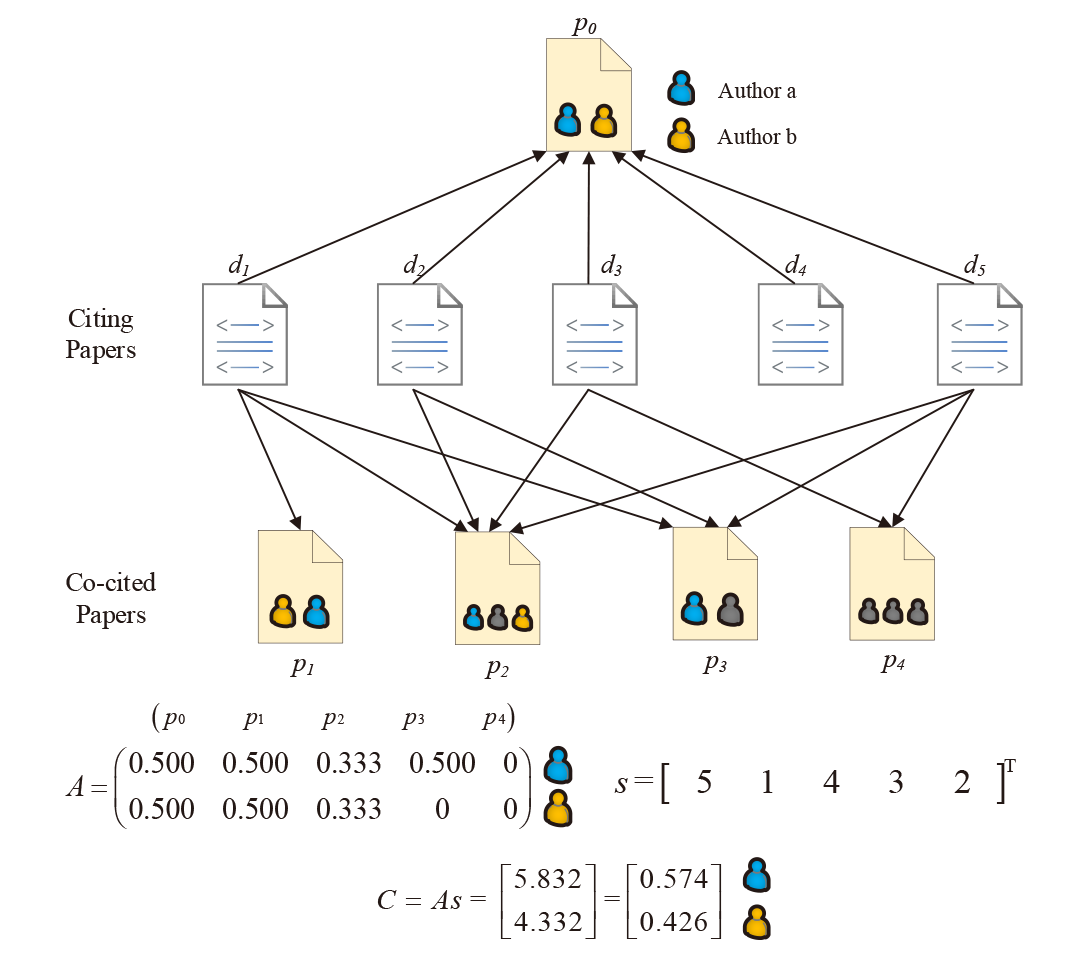
Figure 1. Collective Credit Allocation (CCA) algorithm. The credits of author A and author B are given by the product of the author involvement matrix A and the co-citation strength vector s. |
Two extreme cases may help us understand the idea behind the CCA algorithm. If author A does not participate in any co-cited papers, the algorithm will assign author B as the leading author of the target paper. If author A and author B always appear together in co-cited papers, the algorithm will designate both authors as the owners of the target paper. In general, the ownership identified falls somewhere between these two extreme examples. Author A and author B have some research collaborations, as well as collaborations with other authors on similar research topics.
Since the development of CCA, other variants are introduced aiming to improve the allocation accuracy from different perspectives. All of these algorithms focus on the modification of the involvement matrix A and the strength vector s. CCA considers that all citing papers have the same importance. Hence, the element in vector s is the number of citing papers that cite the co-cited papers, or equivalently the number of co-citations. In the NCCA algorithm, F. H. Wang et al. (2019) consider that citing papers with more citations is more important. The element value of s is calculated by summing up citations of citing papers that cite the co-cited paper. In the DCA algorithm, Bao et al. (2017) adjust the involvement matrix A by multiplying it by a residual influence Φ. The idea is that the importance of a paper would gradually decrease with time, which is captured by Φ. DCA uses the same strength vector s as that in CCA. The final credits of the co-authors are determined by the product of the author involvement matrix A, residual influence Φ, and the strength vector s. J. P. Wang et al. (2019) propose IDCA method that uses the same residual influence Φ as that in DCA but modifies the strength vector s. The element value of s is calculated by summing over the product of the PageRank value and the citation number of the citing paper. Xing et al. (2021) propose the CoCA method that modifies the collection of papers in matrix A and the value of the strength vector s. CoCA focuses on the subsequent works by co-authors of the target paper (papers authored by at least one of the co-authors). These subsequent papers generate the involvement matrix A. For each subsequent paper, its weight in s is calculated as the number of times that the subsequent paper and target paper use the same reference paper.
While all these methods demonstrate reasonable accuracy in determining the Nobel laureates, they present several limitations that can be addressed. First, the number of citations (or co-citations) is commonly utilized to calculate the strength vector s. But the number of citations usually follows a scale-free distribution. Therefore, s can be skewed towards some extreme values. Furthermore, most of these methods are tested in citation networks composed of APS publications. It is important to extend the analyses to a bigger and more comprehensive dataset such as the MAG dataset. These methods usually give very close credit scores of different co-authors, making the leading author of the paper not very distinguishable from others. Finally, as citations can be intentionally added to the target paper, it is important to perform the robustness test, which is not well emphasized in past studies.
3 Data
We utilize two mainstream scholar data sets in this paper. The APS dataset is from 11 Physical Review journals launched by the American Physical Society, covering the period from 1893 to 2009, with a total of 463,332 papers, 4,710,547 citation pairs, and 247,974 author information. The Microsoft Academic Graph (MAG) dataset, covers 71 academic fields, 224,876,396 papers, 1,492,784,521 citation pairs, and 236,021,246 author information. To avoid author name ambiguity, we apply Rule-matching Name-disambiguation (Jia et al., 2017; Sinatra et al., 2016) to disambiguate the author information in the APS dataset. We extract the full name of their last name, first name, and middle name initials for uniform replacement. For the MAG dataset, we directly use the disambiguated author names in the data.
We select the Nobel Prize-winning paper in Physics used in previous studies (Bao et al., 2017; F. H. Wang et al., 2019; J. P. Wang et al., 2019; Shen et al., 2014; Xing et al., 2021) as the validation dataset to verify the accuracy of our algorithm. Totally, there are 30 Nobel Prize-winning papers considered by past studies. After removing papers with only one author and papers that all co-authors receive laureates, 24 multi-author papers were retrieved in the APS dataset and 22 in the MAG dataset. Details can be found in Appendix Tables S1 and S2.
At the same time, we extract 654,148 papers in the field of computer science in the MAG dataset to validate the distinguishability of identified paper owners.
4 Method
In this work, we propose the Nonlinear Collective Credit Allocation with a modified Sigmoid (NCCAS) algorithm (Figure. 2 ). NCCAS is similar to NCCA, which takes the citation number of the citing paper into consideration. Compared with other related methods, NCCAS introduces two major modifications.
First, to handle extreme values in citation counts and to make the distribution of element values in s bounded, we introduce a modified Sigmoid function (Eq. (1)) that transfers the citation counts to the weight of a paper. The parameter α in Eq. (1) is the average number of citations that the citing papers receive. In the ablation experiment of this paper, we show that the average value gives the most accurate identification of the Nobel laureates compared with the use of median and mode values. The parameter n is the average number of citations of all papers considered. The value varies with different tasks and datasets used. For example, for the task of identifying Nobel laureates, we have n = 20.813 in the APS dataset and n = 22.383 in the MAG dataset. When applying NCCAS to 654,148 papers in computer science, we have n = 13.086. In general, the parameter α sets the scale of citing papers that cites the same target paper and n sets the scale of the whole data considered.
$S(x)=\dfrac{1}{1+e^{-\frac{x}{\alpha}}}*Factor,Factor=\begin{cases}\dfrac{1}{\alpha},x=0,orx\ge n\\\dfrac{x}{\alpha},0<x<n\end{cases}$
With Eq. (1) that rescales the citation counts, the element value of the strength vector s can be calculated as si=∑j∈JS(xj), where i represents a co-cited paper, J is the set of citing papers that cite the co-cited paper i, and xj is the number of citations of the citing paper j.
The second modification is the removal of the target paper in the involvement matrix A and the strength vector s. This is because that all citing papers are associated with the target paper. Hence, the target paper will have the largest value in strength vector s. Consequently, keeping the target paper in A will dilute the contributions of co-cited papers, making the credit score C less sensitive to co-citing papers. In the ablation experiment, we show that the removal of the target paper itself in calculating C will make the identified leading author more distinguishable from others.
Taken together, as shown in Figure 2 , the procedure of NCCAS is as follows:
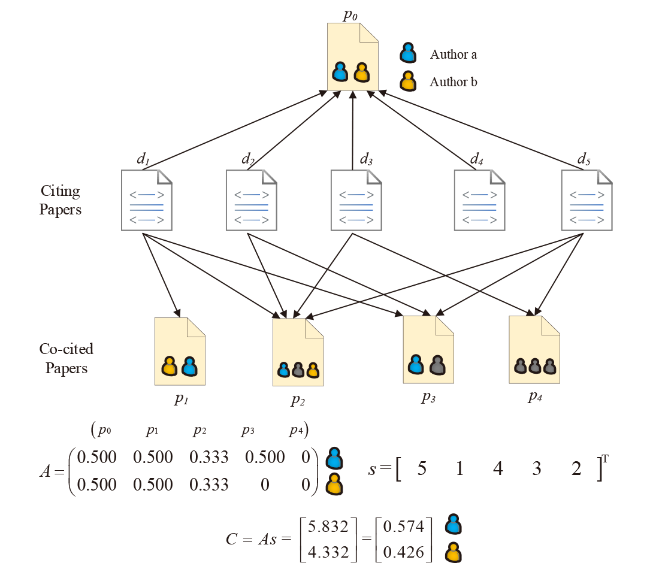
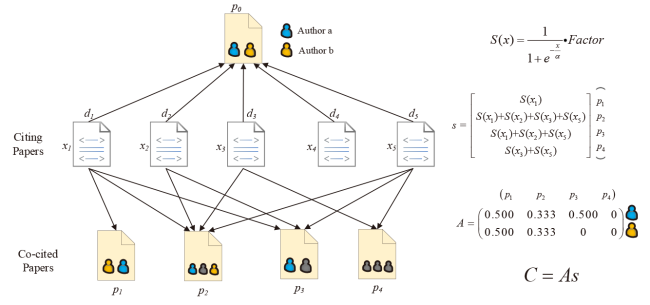
Figure 2. Nonlinear Collective Credit Allocation with Sigmoid Function (NCCAS) algorithm based on the co-citation network. p0 is the target paper, pk (k=1~4) are the co-cited papers, and d1~d5 cite both p0 and p1~p4. xm is the number of citations dm receives. The matrix A records the authorship involvement of the co-authors in the co-cited paper pk. The co-citation strength vector s captures the co-citation strength from the citing papers dm to the target paper p0 and the co-cited paper pk. S(x) is the modified Sigmoid Function. After obtaining matrix A and vector s, the values of the co-authors’ contributions C in the target paper p0 are computed by C=As with a normalization, where P is the co-cited paper set, ci is the credit of co-author ai in target paper p0. |
1. Find all the papers that cite the target paper p0, forming the set of citing papers set D=(d0, d1, …, dm).
2. Find all the papers that are authored by at least one author of the target paper. Among them, find the set of co-cited papers, P=(p1, p2,…, pk), that are cited with the target paper by the citing paper.
3. Calculate the strength vector s for the co-cited papers. The element value si is the sum of the transformed weight of citing papers that cite the co-cited paper i. For example, for the co-cited paper p2 in Figure 2 , we have s2=S(x1)+S(x2)+S(x3)+S(x5), as four papers (d1, d2, d3, d5) cite both the target paper p0 and the co-cited paper p2.
4. Generate the authorship involvement matrix A by calculating the authorship credit of an author in co-cited papers. The authorship credit value is calculated using the fractional counting method. If author a, one of the authors in the target paper, appears in a co-cited paper with a total of three authors, the authorship credit of author a in this co-cited paper is 1/3.
5. The credit shares of all co-authors in the target paper p0 are given by vector C=As. By normalizing vector C, we can obtain the credit shares of co-authors in fractional form.
5 Results
5.1 Validation
The scientific community lacks a unified standard for determining authorship attribution, making it difficult to find instances with known credit allocation results to validate the allocation method. Previous studies (Bao et al., 2017; F. H. Wang et al., 2019; J. P. Wang et al., 2019; Shen et al., 2014; Xing et al., 2021) consider papers receiving the Nobel Physics Prize as the validation set to verify the accuracy of the algorithms. Indeed, the choice of Nobel Prize winners reflects the scientific community’s recognition: the author who makes the most contribution to the Nobel Prize-winning papers is considered as the rightful owner of the scientific achievement (Lo, 2013).
Because the Nobel Physics Prize can be awarded to a maximum of three authors and two different scientific discoveries each year, there are cases when multiple authors of a Nobel Prize-winning paper receive the award. In addition, previous studies use different evaluation criteria. For example, if the algorithm gives two tied candidates and one of them is the Nobel laureate, do we consider the result 100% accurate or just 50% accurate? Likewise, if a paper has two Nobel laureates and the top-two candidates by the algorithm cover only one Nobel laureate, how do gauge the accuracy of the allocation result? To unify different cases and provide a comprehensive comparison of different algorithms, we consider two scenarios in this paper.
Whole counting: the output of the algorithm is considered correct if one of the identified leading authors of the paper is the true Nobel laureate. For example, if the algorithm gives two tied candidates and one of them is the true Nobel laureate, or if two authors of the paper are Nobel laureates and the algorithm identifies one of them in the top-two candidates, we consider the output of the algorithm is one-hundred-percent correct. This is the most commonly adopted evaluation criterion in past studies.
Fractional counting: we use a variant of Jaccard similarity to calculate the fractional overlap between the algorithm output and the ground truth. Assuming that the algorithm predicts a set of leading authors M1 and true Nobel laureates set is M2,we evaluate the result using $ \frac{\mid M_{_1}\cap M_{_2}\mid}{\mid M_{_1}\mid}$. The fractional counting provides a more comprehensive evaluation when there are tied owners or multiple Nobel laureates of a given paper.
Based on the two evaluation criteria, we compare the number of papers whose leading author is successfully recognized by NCCAS and other baseline methods. The statistics are shown in Table 1 and the detailed values for each paper are shown in Appendix Table S1 and Appendix Table S2. Note that we only retrieve 22 papers in the APS dataset and six papers in the MAG dataset that are applicable for CoCA, so we also calculate the percentage accuracy for CoCA and NCCAS.
Table 1. The number of papers identified by different allocation methods under the scenarios “Whole” and “Fractional” evaluations. |
| Dataset | Numbers | |||||
|---|---|---|---|---|---|---|
| CCA | NCCA | DCA | CoCA | NCCAS | ||
| Whole | APS(24) | 17 | 20 | 20 | 17(77.27%) | 20(83.33%) |
| MAG(22) | 18 | 18 | 18 | 4(66.67%) | 19(86.36%) | |
| Fractional | APS(24) | 16.08 | 19.08 | 17.58 | 15.25(69.32%) | 19.58(81.58%) |
| MAG(22) | 17.67 | 16.33 | 14.31 | 4(66.67%) | 18.67(84.86%) | |
The proposed NCCAS performs well in both datasets under both evaluation criteria. NCCAS is based on NCCA, but the introduction of the Sigmoid function improves the identification accuracy. This is mainly because NCCAS can take into account citing papers with zero citation while NCCA ignores their contributions. The removal of the target paper makes the leading author more distinguishable and effectively reduces tied outputs. Hence, the performance of NCCAS is also stable under the fractional counting.
5.2 Distinguishability
To quantify the extent that the output of the first and second candidates are separated, we consider the credit share difference between the highest and the second highest credit scores (denoted as Δ). The larger the value of Δ, the easier to distinguish the leading author.
We first analyze Δ values for Nobel Prize-winning papers in the APS dataset (Table 2 ). In most cases, ∆ by NCCAS is the largest. In a few cases when NCCAS is not the largest, its Δ value is the second largest. It is also noteworthy that except in one paper that all algorithms give the same tied results, NCCAS does not give ties, while NCCA, DCA, and CoCA all yield ties in different papers. Table 2 clearly shows that NCCAS makes the leading author of the Nobel Prize-winning paper more distinguishable compared with other methods.
Table 2. ∆ by different methods for the Nobel Prize-winning papers in Physics (APS dataset). |
| DOI | The value of Δ | ||||
|---|---|---|---|---|---|
| CCA | NCCA | DCA | CoCA | NCCAS | |
| 10.1103/PhysRevLett.76.1796 | 0.033 | 0.013 | 0.001 | 0.046 | 0.094 |
| 10.1103/PhysRevLett.84.5102 | 0.021 | 0.014 | 0.006 | 0.031 | 0.035 |
| 10.1103/PhysRevLett.77.4887 | 0.002 | 0.002 | 0.001 | 0.011 | 0.004 |
| 10.1103/PhysRevLett.55.48 | 0.19 | 0.12 | 0.149 | 0.268 | 0.385 |
| 10.1103/PhysRevLett.61.2472 | 0.152 | 0.067 | 0.005 | 0.156 | 0.72 |
| 10.1103/PhysRevLett.75.3969 | 0.042 | 0.004 | 0.002 | 0.122 | 0.345 |
| 10.1103/PhysRevLett.13.138 | 0.02 | 0.002 | 0.0 | 0.0 | 0.154 |
| 10.1103/PhysRev.69.37 | 0.204 | 0.051 | 0.257 | 0.25 | 0.561 |
| 10.1103/PhysRev.83.333 | 0.009 | 0.002 | 0.015 | 0.022 | 0.183 |
| 10.1103/PhysRevLett.61.169 | 0.05 | 0.023 | 0.059 | 0.053 | 0.263 |
| 10.1103/PhysRevLett.13.321 | 0.006 | 0.0 | 0.002 | 0.0 | 0.6 |
| 10.1103/PhysRev.122.345 | 0.078 | 0.01 | 0.002 | 0.364 | 0.908 |
| 10.1103/PhysRevLett.57.2442 | 0.077 | 0.018 | 0.003 | 0.193 | 0.306 |
| 10.1103/PhysRevLett.84.3232 | 0.052 | 0.032 | 0.008 | 0.076 | 0.193 |
| 10.1103/PhysRevLett.20.1205 | 0.128 | 0.005 | 0.071 | 0.167 | 0.698 |
| 10.1103/PhysRevLett.58.1490 | 0.003 | 0.0 | 0.023 | - | 0.012 |
| 10.1103/PhysRevLett.48.1559 | 0.06 | 0.081 | 0.006 | 0.319 | 0.297 |
| 10.1103/PhysRevLett.61.826 | 0.025 | 0.013 | 0.032 | 0.048 | 0.235 |
| 10.1103/PhysRevLett.35.1489 | 0.002 | 0.001 | 0.001 | 0.0 | 0.006 |
| 10.1103/PhysRevLett.9.439 | 0.0 | 0.0 | 0.0 | - | 0.0 |
| 10.1103/PhysRev.72.241 | 0.182 | 0.036 | 0.144 | 0.25 | 0.636 |
| 10.1103/PhysRev.112.1940 | 0.008 | 0.032 | 0.0 | 0.368 | 0.654 |
| 10.1103/PhysRev.73.679 | 0.024 | 0.003 | 0.004 | 0.071 | 0.066 |
| 10.1103/PhysRevD.5.528 | 0.088 | 0.001 | 0.006 | 0.241 | 0.059 |
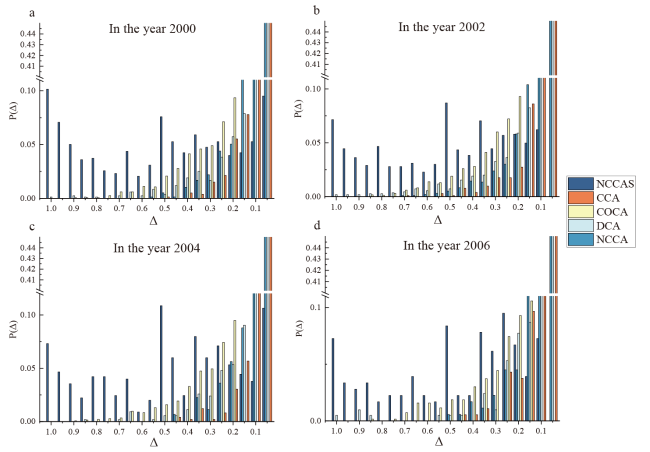
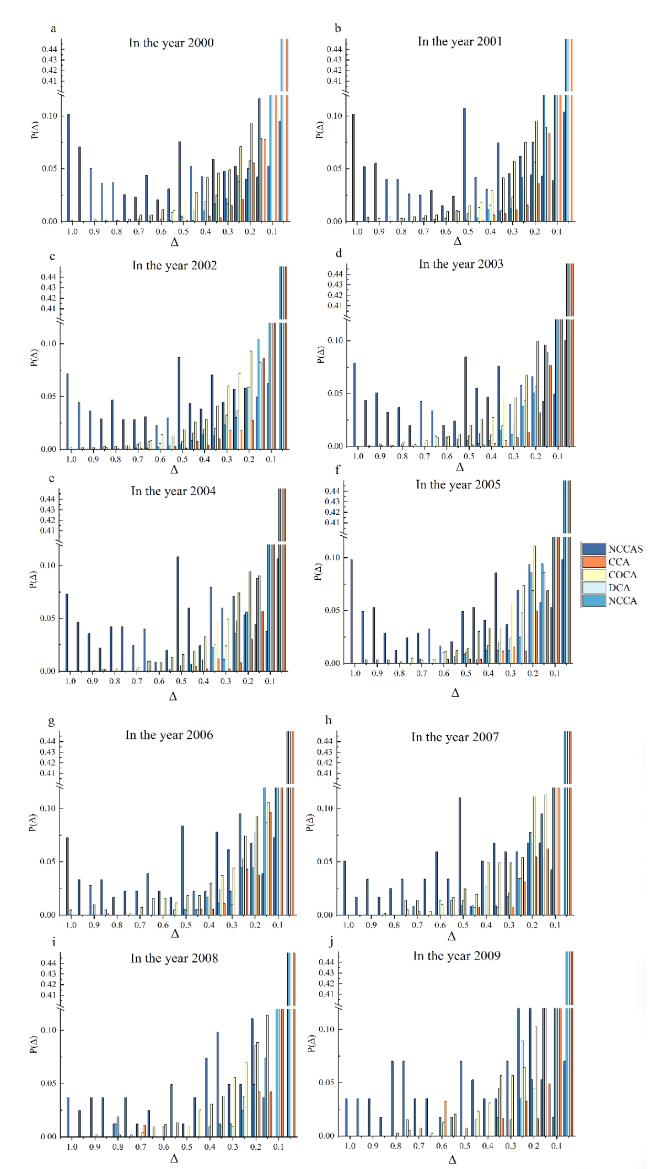
Figure 3. The distribution of Δ by different methods for papers published in different years. |
To go beyond the Nobel Prize-winning papers and to demonstrate the overall situation of how distinguishable the identified leading author is, we select 654,148 papers in computer science and calculate the Δ values by different methods (Figure 3 ). The result of all years is shown in Appendix Figure S1. Δ values by CCA, NCCA, DCA, and CoCA tend to be concentrated in the [٠, ٠.٣] interval, but over ٤٠٪ of results by NCCAS have Δ values greater than ٠.٥. Hence, for general publication data, NCCAS still makes the leading author of the paper distinguishable from others.
5.3 Robustness
As one can intentionally create citing papers that cite the target and co-cited papers, it is important to check the robustness of the results by different methods under malicious manipulation. For example, F. H. Wang et al. (2019) show that by citing a small number of additional papers to the target paper, it is possible to significantly change the authorship credit by the CCA method. For this reason, we consider a simple experiment in which papers with a certain number of citations are added that cites the target paper and one randomly chosen co-cited paper. We measure the number of papers needed to invert the rank of the credit score that makes the one originally with the second highest score become the leading author. We consider two different cases: papers with 20 citations are added and papers with one citation are added. The choice of 20 citations is based on the fact that the average number of citations in the APS dataset is about 20. The case for one citation is because the average citation after one year of publication is about one in the APS dataset. Note that only NCCAS and NCCA consider the number of citations. CCA and DCA consider all citing papers to be equally important. Hence, they are not affected by the citing papers’ number of citations.
We first focus on the 24 Nobel Prize-winning papers in the APS dataset. Because the added papers cite the co-cited papers randomly, we repeat the experiment ten times and show in Table 3 the average number of papers needed to invert the original credit score rank. Methods that take the number of citations into account (NCCASand NCCA) are more robust than those that do not consider citations (CCA and DCA). This is in line with conclusions in previous studies (F. H. Wang et al., 2019). In most cases, NCCAS is more robust than NCCA. We also check the cases when NCCAS is less robust than NCCA (four papers 10.1103/PhysRevLett.55.48, 10.1103/PhysRevLett.69.37, 10.1103/PhysRev.83.333, and 10.1103/PhysRev.73.679). We find that these papers have citing papers with an extreme number of citations. Because the original citing papers’ citations are very high, adding papers with 1 or 20 citations will not significantly change the strength vector. Therefore, in these cases NCCA is more robust than NCCAS.
Table 3. The number of added papers with different citations to invert the credit rank for 24 Nobel Prize-winning papers. |
| DOI | CCA | DCA | Added papers with 20 citations | Added papers with 1 citation | ||
|---|---|---|---|---|---|---|
| NCCA | NCCAS | NCCA | NCCAS | |||
| 10.1103/PhysRevLett.76.1796 | 66 | 42 | 106 | 132 | 2,109 | 10,018 |
| 10.1103/PhysRevLett.84.5102 | 15 | 6 | 10 | 28 | 190 | 1,348 |
| 10.1103/PhysRevLett.77.4887 | 5 | 5 | 2 | 15 | 39 | 1,943 |
| 10.1103/PhysRevLett.55.48 | 53 | 15 | 164 | 29 | 3,264 | 1,294 |
| 10.1103/PhysRevLett.61.2472 | 565 | 580 | 808 | 1,208 | 10,100 | 10,100 |
| 10.1103/PhysRevLett.75.3969 | 475 | 446 | 982 | 985 | 10,100 | 10,100 |
| 10.1103/PhysRevLett.13.138 | 44 | 35 | 42 | 66 | 823 | 838 |
| 10.1103/PhysRev.69.37 | 51 | 30 | 107 | 40 | 2,135 | 2,031 |
| 10.1103/PhysRev.83.333 | 4 | 1 | 32 | 1 | 34 | 1 |
| 10.1103/PhysRevLett.61.169 | 37 | 4 | 7 | 53 | 135 | 2,860 |
| 10.1103/PhysRevLett.13.321 | 5 | 1 | 3 | 4 | 50 | 966 |
| 10.1103/PhysRev.122.345 | 443 | 293 | 737 | 757 | 10,100 | 10,100 |
| 10.1103/PhysRevLett.57.2442 | 146 | 150 | 171 | 252 | 3,413 | 10,100 |
| 10.1103/PhysRevLett.84.3232 | 15 | 11 | 17 | 25 | 322 | 468 |
| 10.1103/PhysRevLett.20.1205 | 96 | 96 | 106 | 174 | 2,120 | 10,100 |
| 10.1103/PhysRevLett.58.1490 | 20 | 21 | 17 | 52 | 47 | 10,100 |
| 10.1103/PhysRevLett.48.1559 | 196 | 197 | 314 | 369 | 6,261 | 10,100 |
| 10.1103/PhysRevLett.61.826 | 20 | 18 | 57 | 88 | 1,127 | 10,100 |
| 10.1103/PhysRevLett.35.1489 | 9 | 13 | 17 | 26 | 327 | 2,881 |
| 10.1103/PhysRevLett.9.439 | 1 | 1 | 1 | 1 | 1 | 1 |
| 10.1103/PhysRev.72.241 | 99 | 88 | 179 | 212 | 3,569 | 10,100 |
| 10.1103/PhysRev.112.1940 | 18 | 16 | 31 | 33 | 604 | 1,656 |
| 10.1103/PhysRev.73.679 | 37 | 1 | 89 | 74 | 1,762 | 1,655 |
| 10.1103/PhysRevD.5.528 | 68 | 23 | 55 | 57 | 1,093 | 3,219 |
We further run the experiment in papers in the MAG dataset by selecting 654,148 papers in computer science. We add citing papers with 13 citations, which is the average number of citations in the data analyzed. In Figure 4 , we show the distribution of the number of papers needed to invert the original credit rank. The result of all years is shown in Appendix Figure S2. The distributions of CCA and DCA are more concentrated on small counts of added papers, while the distributions of NCCA and NCCAS have a high portion for a large number of added papers. The robustness of NCCAS is higher than NCCA as the distribution of NCCAS is more skewed towards a large number of added papers. The analysis on large-scale papers is in line with results on Nobel Prize-winning papers that NCCAS is in general more robust towards manipulations compared with other baseline methods.
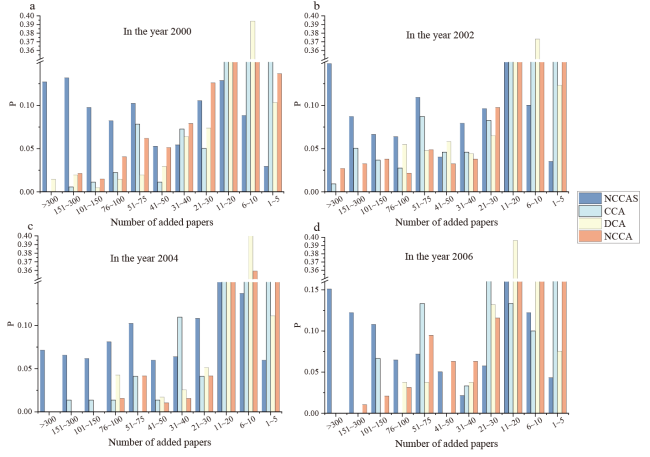
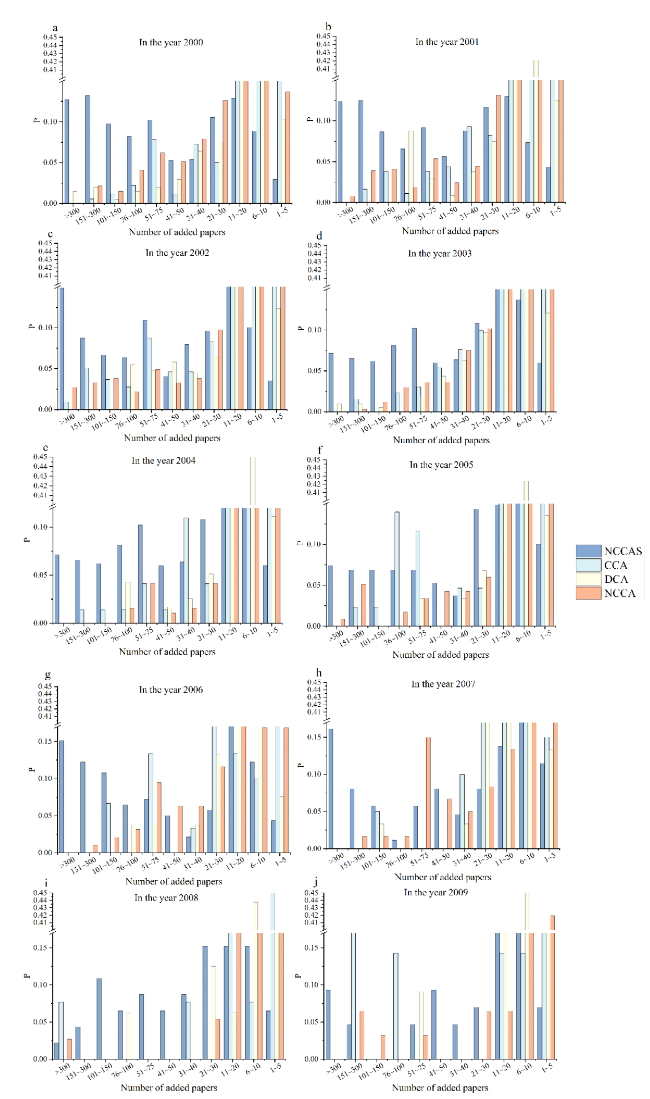
Figure 4. The distribution of the number of added papers by different methods for papers published in different years. |
6 Ablation experiment
In this part, we perform different experiments to explain the reason for the modifications that NCCAS makes, and the reason for the choice of some parameters.
6.1 Removal of the target paper
A major modification made in NCCAS is that the target paper is not included in the author involvement matrix A and strength vector s. To quantitatively show the effect of this removal, we build a NCCAS-T method that is the same with NCCAS but keep the target paper in matrix A. The results on the leading author identification and the Δ value for the 24 Nobel Prize-winning papers in the APS dataset are shown in Table 4 . The removal does not change the identification results. The author with the highest credit score remains the same. But because the target paper dilutes the contribution of other co-cited papers, results by NCCAS-T are not as distinguishable as those by NCCAS. Therefore, removing the target paper’s contribution is crucial for NCCAS’s improved distinguishability.
Table 4. The leading author identification and the Δ values for 24 Nobel Prize-winning papers by methods NCCAS and NCCAS-T in the APS dataset. NCCAS-T refers to the method that keep the target paper in the author involvement matrix. |
| DOI | NCCAS-T | NCCAS | NCCAS-T | NCCAS |
|---|---|---|---|---|
| If accurate (Y/N) | Δ value | |||
| 10.1103/PhysRevLett.76.1796 | Y | Y | 0.002 | 0.094 |
| 10.1103/PhysRevLett.84.5102 | Y | Y | 0.012 | 0.035 |
| 10.1103/PhysRevLett.77.4887 | Y | Y | 0.001 | 0.004 |
| 10.1103/PhysRevLett.55.48 | N | N | 0.017 | 0.385 |
| 10.1103/PhysRevLett.61.2472 | Y | Y | 0.002 | 0.72 |
| 10.1103/PhysRevLett.75.3969 | Y | Y | 0.002 | 0.345 |
| 10.1103/PhysRevLett.13.138 | Y | Y | 0.001 | 0.154 |
| 10.1103/PhysRev.69.37 | N | N | 0.002 | 0.561 |
| 10.1103/PhysRev.83.333 | N | N | 0.112 | 0.183 |
| 10.1103/PhysRevLett.61.169 | Y | Y | 0.003 | 0.263 |
| 10.1103/PhysRevLett.13.321 | Y | Y | 0.007 | 0.6 |
| 10.1103/PhysRev.122.345 | Y | Y | 0.01 | 0.908 |
| 10.1103/PhysRevLett.57.2442 | Y | Y | 0.008 | 0.306 |
| 10.1103/PhysRevLett.84.3232 | Y | Y | 0.037 | 0.193 |
| 10.1103/PhysRevLett.20.1205 | Y | Y | 0.027 | 0.698 |
| 10.1103/PhysRevLett.58.1490 | N | N | 0.002 | 0.012 |
| 10.1103/PhysRevLett.48.1559 | Y | Y | 0.027 | 0.297 |
| 10.1103/PhysRevLett.61.826 | Y | Y | 0.017 | 0.048 |
| 10.1103/PhysRevLett.35.1489 | Y | Y | 0.003 | 0.235 |
| 10.1103/PhysRevLett.9.439 | Y | Y | 0.0 | 0.0 |
| 10.1103/PhysRev.72.241 | Y | Y | 0.284 | 0.636 |
| 10.1103/PhysRev.112.1940 | Y | Y | 0.002 | 0.654 |
| 10.1103/PhysRev.73.679 | Y | Y | 0.004 | 0.066 |
| 10.1103/PhysRevD.5.528 | Y | Y | 0.001 | 0.059 |
6.2 The calculation of the authorship involvement matrix A
In all the methods including NCCAS and fractional counting (Van Hooydonk, 1997) is used to construct the authorship involvement matrix A. If the co-cited paper has N authors, then the corresponding element value in A is 1/N. In this section, we explore whether different weight allocations for the authorship involvement matrix would make any difference. Besides fractional counting, we check first last author emphasis method (Tscharntke et al., 2007), sequence determines credit method (Verhagen et al., 2003), harmonic counting (Hagen, 2008; 2010), geometric counting (Egghe et al., 2000), and arithmetic counting (Trueba et al., 2004). The results are shown in Table 5 .
Table 5. The identification of Nobel laureates by different authorship involvement matrices with fractional counting. |
| Method | Numbers | ||||
|---|---|---|---|---|---|
| CCA | NCCA | DCA | CoCA | NCCAS | |
| fractional counting | 16.08 | 19.08 | 17.58 | 15.25 | 19.58 |
| first last author emphasis | 16.5 | 17 | 16 | 15.67 | 17.67 |
| sequence determines credit | 15.67 | 16 | 16 | 15 | 16.67 |
| harmonic counting | 15 | 16.33 | 16 | 14.67 | 17 |
| geometric counting | 14.33 | 15 | 15 | 14.33 | 14 |
| arithmetic counting | 13 | 15 | 14 | 11.33 | 11.67 |
The optimal choice for authorship involvement matrix calculation differs in different methods. It is interesting to note that while fractional counting is adopted by the first relevant method CCA, it is not the most optimal choice. But in general, fractional counting works well in all different algorithms. Table 6 supports the choice of authorship involvement matrix of NCCAS.
Table 6. The identification of Nobel laureates by different rescale functions. |
| Dataset | Numbers | |||||
|---|---|---|---|---|---|---|
| NCCAS | S2(x)(β=2) | S2(x)(β=e) | S2(x)(β=5) | S2(x)(γ=1.3) | ||
| Whole | APS(24) | 20 | 20 | 20 | 20 | 20 |
| MAG(22) | 19 | 18 | 18 | 18 | 18 | |
| Fractional | APS(24) | 19.58 | 12.15 | 12.15 | 12.15 | 16.34 |
| MAG(22) | 18.67 | 17.83 | 17.83 | 17.83 | 16.83 | |
6.3 Selection of the rescale function
We use a modified Sigmoid function to transfer the number of citations to the relative importance of a citing paper. The aim of the Sigmoid function is to rescale the number of citations such that extreme values would play a less important role. However, other forms of function may also work. In this section, we consider the logarithmic function (Eq. (2)) and power-law function (Eq. (3)) to characterize relative importance and check if these functions would improve the performance. For the logarithmic function, we choose the parameter β=2,e,5. For the power-law function, we choose γ=1.3, which is opposite to the citation distribution of citing papers related to the Nobel Prize-winning papers in the APS dataset (Appendix Figure S3).
S2(x)=logβx
S3(x)=xγ
The identification performance by different rescale functions is shown in Table 6 . The modified Sigmoid function in NCCAS makes more accurate identifications of Nobel laureates compared with the other two types of functions. In particular, the logarithmic function and power-law function often yield authors with tied credit. Their performance is even worse when the fractional counting is used to quantify the performance. These results demonstrate that the Sigmoid function is a better choice compared with other forms of function.
6.4 The calculation of parameter α
The parameter α is calculated as the average citation counts of the citing paper. In this section, we compare the average value with the median and mode values. The performance of Nobel laureate identification in the APS dataset by different choices is shown in Table 7 . When α takes the average value, the performance is the best.
Table 7. The identification of Nobel laureates by the NCCAS algorithm, when parameter α corresponds to the median, mode, and average. |
| Dataset | Numbers | |||
|---|---|---|---|---|
| Average | Median | Mode | ||
| Whole | APS(24) | 20 | 19 | 19 |
| MAG(22) | 19 | 18 | 18 | |
| Fractional | APS(24) | 19.58 | 17.25 | 17.67 |
| MAG(22) | 18.67 | 17.125 | 17.33 | |
7 Conclusion
To summarize, we propose the NCCAS method to allocate credit for each co-author and identify the leading author of a multi-author publication. We introduce a modified Sigmoid function to rescale the citation number of the citing papers. We remove the target paper in the calculation of the credit share. Compared with other credit allocation methods, NCCAS gives the best performance in identifying Nobel laureates in both the APS and the MAG datasets. In addition, the leading author identified is well separated from other co-authors in terms of their credit scores, providing an improved distinguishability compared with other methods. NCCAS is also more robust under manipulations, which acquires the largest number of added papers to invert the leading author. These features make NCCAS very applicable to large-scale publication data.
Future applications include analyzing the role of a paper’s leading author. It is interesting to check if the leading author tends to be the first author, the last author, or the author with the longest academic age (Drenth, 1998; Hundley et al., 2013; Sekara et al., 2018), and how this pattern differs in different disciplines. The identification of a paper’s leading author would help in the study of a scientist’s research agenda (Huang et al., 2023; S. Huang et al., 2022; X. Yu et al., 2021). Taking only publications led by a scientist will reduce the influence of papers that he/she participates in with less significant roles. Finally, identifying the leading author can also help understand the formation and the structure of a scientific team (Milojević, 2014; Yu et al., 2022). NCCAS can be a useful tool to address these questions.
Funding information
This work was supported by University Innovation Research Group of Chongqing (No.CXQT21005).
Author contributions
Yang Li (Yang52h@163.com) proposed the original idea, carried out the experiment, and wrote the manuscript. Tao Jia (tjia@swu.edu.cn) analyzed and reviewed the manuscript. All authors contributed comments on the results and revisions to the final version.
Appendix
Table S1. The credits of Nobel Prize-Winning papers identified by the algorithms (APS dataset). All Nobel Prize winners in physics and their work owners have their scores bolded. |
| DOI | Author Name | CCA | NCCA | DCA | COCA | NCCAS |
|---|---|---|---|---|---|---|
| 10.1103/ PhysRevLett.76.1796 | D. M. Meekhof | 0.149 | 0.179 | 0.196 | 0.154 | 0.050 |
| C. Monroe | 0.181 | 0.191 | 0.201 | 0.16 | 0.143 | |
| B. E. King | 0.159 | 0.182 | 0.197 | 0.154 | 0.071 | |
| W. M. Itano | 0.239 | 0.218 | 0.203 | 0.243 | 0.321 | |
| D. J. Wineland | 0.272 | 0.231 | 0.204 | 0.289 | 0.415 | |
| 10.1103/ PhysRevLett.84.5102 | S. A. Diddams | 0.068 | 0.07 | 0.079 | 0.075 | 0.039 |
| D. J. Jones | 0.050 | 0.048 | 0.072 | 0.075 | 0.0 | |
| J. Ye | 0.102 | 0.132 | 0.094 | 0.075 | 0.016 | |
| S. T. Cundiff | 0.050 | 0.048 | 0.072 | 0.075 | 0.0 | |
| J. L. Hall | 0.104 | 0.162 | 0.095 | 0.075 | 0.217 | |
| J. K. Ranka | 0.057 | 0.057 | 0.073 | 0.075 | 0.018 | |
| R. S. Windeler | 0.061 | 0.068 | 0.08 | 0.075 | 0.035 | |
| R. Holzwarth | 0.149 | 0.103 | 0.138 | 0.138 | 0.105 | |
| T. Udem | 0.170 | 0.137 | 0.152 | 0.169 | 0.175 | |
| T. W. H nsch | 0.191 | 0.176 | 0.146 | 0.169 | 0.252 | |
| 10.1103/ PhysRevLett.77.4887 | M. Brune | 0.207 | 0.195 | 0.13 | 0.203 | 0.263 |
| E. Hagley | 0.080 | 0.071 | 0.122 | 0.068 | 0.019 | |
| J. Dreyer | 0.069 | 0.065 | 0.121 | 0.068 | 0.007 | |
| X. Ma tre | 0.073 | 0.068 | 0.122 | 0.068 | 0.013 | |
| A. Maali | 0.076 | 0.073 | 0.122 | 0.11 | 0.022 | |
| C. Wunderlich | 0.074 | 0.080 | 0.122 | 0.068 | 0.036 | |
| J. M. Raimond | 0.211 | 0.223 | 0.131 | 0.203 | 0.318 | |
| S. Haroche | 0.209 | 0.225 | 0.131 | 0.214 | 0.322 | |
| 10.1103/ PhysRevLett.55.48 | S. Chu | 0.196 | 0.23 | 0.335 | 0.135 | 0.219 |
| L. Hollberg | 0.096 | 0.109 | 0.151 | 0.35 | 0.0 | |
| J. E. Bjorkholm | 0.162 | 0.168 | 0.159 | 0.163 | 0.119 | |
| A. Cable | 0.16 | 0.142 | 0.168 | 0.135 | 0.058 | |
| A. Ashkin | 0.386 | 0.35 | 0.186 | 0.431 | 0.604 | |
| 10.1103/ PhysRevLett.61.2472 | M. N. Baibich | 0.092 | 0.101 | 0.11 | 0.311 | 0.0 |
| J. M. Broto | 0.093 | 0.101 | 0.11 | 0.155 | 0.007 | |
| A. Fert | 0.252 | 0.178 | 0.116 | 0.103 | 0.832 | |
| F. N. Van Dau | 0.093 | 0.105 | 0.111 | 0.078 | 0.049 | |
| F. Petroff | 0.1 | 0.111 | 0.111 | 0.062 | 0.112 | |
| P. Etienne | 0.092 | 0.101 | 0.11 | 0.052 | 0.0 | |
| G. Creuzet | 0.092 | 0.101 | 0.11 | 0.044 | 0.0 | |
| A. Friederich | 0.092 | 0.101 | 0.11 | 0.039 | 0.0 | |
| J. Chazelas | 0.092 | 0.101 | 0.11 | 0.155 | 0.0 | |
| 10.1103/ PhysRevLett.75.3969 | K. B. Davis | 0.101 | 0.142 | 0.142 | 0.134 | 0.056 |
| M. -O. Mewes | 0.093 | 0.141 | 0.142 | 0.134 | 0.0 | |
| M. R. Andrews | 0.16 | 0.143 | 0.143 | 0.134 | 0.161 | |
| N. J.vanDruten | 0.153 | 0.143 | 0.142 | 0.134 | 0.128 | |
| D. S. Durfee | 0.146 | 0.142 | 0.143 | 0.134 | 0.089 | |
| D. M. Kurn | 0.145 | 0.142 | 0.142 | 0.134 | 0.061 | |
| W. Ketterle | 0.202 | 0.147 | 0.145 | 0.193 | 0.506 | |
| 10.1103/ PhysRevLett.13.138 | J.H.Christenson | 0.232 | 0.248 | 0.25 | 0.25 | 0.08 |
| J. W. Cronin | 0.278 | 0.253 | 0.25 | 0.25 | 0.509 | |
| V. L. Fitch | 0.258 | 0.251 | 0.25 | 0.25 | 0.355 | |
| R. Turlay | 0.232 | 0.248 | 0.25 | 0.25 | 0.056 | |
| 10.1103/ PhysRev.69.37 | E. M. Purcell | 0.298 | 0.32 | 0.282 | 0.5 | 0.187 |
| H. C. Torrey | 0.199 | 0.309 | 0.179 | 0.25 | 0.065 | |
| R. V. Pound | 0.502 | 0.371 | 0.539 | 0.25 | 0.748 | |
| 10.1103/ PhysRev.83.333 | C. G. Shull | 0.348 | 0.334 | 0.329 | 0.341 | 0.383 |
| W. A. Strauser | 0.294 | 0.33 | 0.326 | 0.319 | 0.051 | |
| E. O. Wollan | 0.357 | 0.336 | 0.344 | 0.341 | 0.566 | |
| 10.1103/ PhysRevLett.61.169 | P. D. Lett | 0.17 | 0.166 | 0.149 | 0.124 | 0.162 |
| R. N. Watts | 0.15 | 0.157 | 0.135 | 0.145 | 0.06 | |
| C. I. Westbrook | 0.161 | 0.163 | 0.248 | 0.124 | 0.126 | |
| W. D. Phillips | 0.22 | 0.189 | 0.189 | 0.268 | 0.425 | |
| P. L. Gould | 0.158 | 0.162 | 0.142 | 0.124 | 0.114 | |
| H. J. Metcalf | 0.142 | 0.162 | 0.137 | 0.215 | 0.114 | |
| 10.1103/ PhysRevLett.13.321 | F. Englert | 0.503 | 0.5 | 0.501 | 0.5 | 0.8 |
| R. Brout | 0.497 | 0.5 | 0.499 | 0.5 | 0.2 | |
| 10.1103/ PhysRev.122.345 | Y. Nambu | 0.539 | 0.505 | 0.501 | 0.682 | 0.954 |
| G. Jona-Lasinio | 0.461 | 0.495 | 0.499 | 0.318 | 0.046 | |
| 10.1103/ PhysRevLett.57.2442 | P. Gr nberg | 0.264 | 0.225 | 0.203 | 0.387 | 0.62 |
| R. Schreiber | 0.186 | 0.192 | 0.2 | 0.194 | 0.066 | |
| Y. Pang | 0.182 | 0.188 | 0.199 | 0.129 | 0.0 | |
| M. B. Brodsky | 0.187 | 0.207 | 0.199 | 0.097 | 0.314 | |
| H. Sowers | 0.182 | 0.188 | 0.199 | 0.194 | 0.0 | |
| 10.1103/ PhysRevLett.84.3232 | J. Reichert | 0.158 | 0.156 | 0.102 | 0.143 | 0.102 |
| M. Niering | 0.09 | 0.144 | 0.083 | 0.08 | 0.03 | |
| R. Holzwarth | 0.174 | 0.165 | 0.228 | 0.108 | 0.157 | |
| M. Weitz | 0.128 | 0.159 | 0.094 | 0.225 | 0.12 | |
| T. Udem | 0.199 | 0.172 | 0.242 | 0.143 | 0.199 | |
| T. W. H_nsch | 0.251 | 0.204 | 0.25 | 0.301 | 0.392 | |
| 10.1103/ PhysRevLett.20.1205 | R. Davis | 0.42 | 0.337 | 0.381 | 0.445 | 0.849 |
| D. S. Harmer | 0.292 | 0.332 | 0.31 | 0.278 | 0.151 | |
| K. C. Hoffman | 0.288 | 0.331 | 0.31 | 0.278 | 0.0 | |
| 10.1103/ PhysRevLett.48.1559 | D. C. Tsui | 0.386 | 0.392 | 0.339 | 0.546 | 0.548 |
| H. L. Stormer | 0.326 | 0.297 | 0.333 | 0.227 | 0.2 | |
| A. C. Gossard | 0.288 | 0.331 | 0.328 | 0.227 | 0.251 | |
| 10.1103/ PhysRevLett.61.826 | A. Aspect | 0.226 | 0.203 | 0.202 | 0.22 | 0.255 |
| E. Arimondo | 0.184 | 0.204 | 0.19 | 0.268 | 0.255 | |
| R. Kaiser | 0.17 | 0.188 | 0.187 | 0.146 | 0.0 | |
| N. Vansteenkiste | 0.17 | 0.188 | 0.187 | 0.146 | 0.0 | |
| C.Cohen-Tan | 0.251 | 0.217 | 0.234 | 0.22 | 0.49 | |
| 10.1103/ PhysRevLett.9.439 | R. Giacconi | 0.25 | 0.25 | 0.25 | - | 0.25 |
| H. Gursky | 0.25 | 0.25 | 0.25 | - | 0.25 | |
| F. R. Paolini | 0.25 | 0.25 | 0.25 | - | 0.25 | |
| B. B. Rossi | 0.25 | 0.25 | 0.25 | - | 0.25 | |
| 10.1103/ PhysRev.72.241 | W. E. Lamb | 0.591 | 0.518 | 0.572 | 0.625 | 0.818 |
| R. C. Retherford | 0.409 | 0.482 | 0.428 | 0.375 | 0.182 | |
| 10.1103/ PhysRev.112.1940 | A. L. Schawlow | 0.504 | 0.484 | 0.5 | 0.316 | 0.173 |
| C. H. Townes | 0.496 | 0.516 | 0.5 | 0.684 | 0.827 | |
| 10.1103/ PhysRev.73.679 | N. Bloembergen | 0.327 | 0.339 | 0.336 | 0.31 | 0.461 |
| E. M. Purcell | 0.322 | 0.326 | 0.331 | 0.31 | 0.143 | |
| R. V. Pound | 0.351 | 0.336 | 0.332 | 0.381 | 0.395 | |
| 10.1103/ PhysRevLett.58.1490 | K. Hirata | 0.039 | 0.043 | 0.033 | - | 0.086 |
| T. Kajita | 0.045 | 0.043 | 0.058 | - | 0.048 | |
| M. Koshiba | 0.045 | 0.043 | 0.034 | - | 0.048 | |
| M. Nakahata | 0.045 | 0.041 | 0.058 | - | 0.044 | |
| Y. Oyama | 0.045 | 0.043 | 0.058 | - | 0.048 | |
| N. Sato | 0.044 | 0.043 | 0.034 | - | 0.041 | |
| A. Suzuki | 0.045 | 0.043 | 0.058 | - | 0.048 | |
| M. Takita | 0.045 | 0.043 | 0.058 | - | 0.048 | |
| Y. Totsuka | 0.045 | 0.043 | 0.058 | - | 0.048 | |
| T. Kifune | 0.044 | 0.043 | 0.034 | - | 0.038 | |
| T. Suda | 0.044 | 0.043 | 0.035 | - | 0.044 | |
| K. Takahashi | 0.044 | 0.044 | 0.034 | - | 0.041 | |
| T. Tanimori | 0.043 | 0.043 | 0.035 | - | 0.032 | |
| K. Miyano | 0.045 | 0.042 | 0.058 | - | 0.048 | |
| M. Yamada | 0.043 | 0.043 | 0.034 | - | 0.029 | |
| E. W. Beier | 0.043 | 0.043 | 0.034 | - | 0.035 | |
| L. R. Feldscher | 0.041 | 0.043 | 0.034 | - | 0.022 | |
| S. B. Kim | 0.043 | 0.043 | 0.058 | - | 0.032 | |
| A. K. Mann | 0.048 | 0.044 | 0.058 | - | 0.098 | |
| F. M. Newcomer | 0.043 | 0.043 | 0.034 | - | 0.035 | |
| R. Van | 0.034 | 0.043 | 0.033 | - | 0.0 | |
| W. Zhang | 0.045 | 0.044 | 0.034 | - | 0.07 | |
| B. G. Cortez | 0.041 | 0.043 | 0.034 | - | 0.019 | |
| 10.1103/ PhysRevD.5.528 | G. Miller | 0.055 | 0.074 | 0.073 | 0.047 | 0.02 |
| E. D. Bloom | 0.18 | 0.077 | 0.086 | 0.312 | 0.188 | |
| G. Buschhorn | 0.045 | 0.073 | 0.073 | 0.038 | 0.006 | |
| D. H. Coward | 0.092 | 0.083 | 0.08 | 0.071 | 0.129 | |
| H. DeStaebler | 0.079 | 0.075 | 0.077 | 0.071 | 0.094 | |
| J. Drees | 0.062 | 0.074 | 0.074 | 0.067 | 0.022 | |
| C. L. Jordan | 0.061 | 0.083 | 0.078 | 0.038 | 0.117 | |
| L. W. Mo | 0.07 | 0.075 | 0.075 | 0.067 | 0.072 | |
| R. E. Taylor | 0.078 | 0.075 | 0.077 | 0.071 | 0.086 | |
| J. I. Friedman | 0.09 | 0.083 | 0.08 | 0.067 | 0.119 | |
| G. C. Hartmann | 0.055 | 0.074 | 0.074 | 0.047 | 0.029 | |
| H. W. Kendall | 0.089 | 0.082 | 0.08 | 0.067 | 0.105 | |
| R. Verdier | 0.044 | 0.073 | 0.073 | 0.038 | 0.003 | |
| 10.1103/ PhysRevLett.35.1489 | M. L. Perl | 0.038 | 0.031 | 0.03 | 0.028 | 0.081 |
| G. S. Abrams | 0.031 | 0.028 | 0.028 | 0.028 | 0.028 | |
| A. M. Boyarski | 0.033 | 0.029 | 0.028 | 0.028 | 0.055 | |
| M. Breidenbach | 0.033 | 0.029 | 0.029 | 0.028 | 0.046 | |
| D. D. Briggs | 0.017 | 0.026 | 0.027 | 0.028 | 0.002 | |
| F. Bulos | 0.028 | 0.028 | 0.028 | 0.028 | 0.028 | |
| W. Chinowsky | 0.028 | 0.028 | 0.029 | 0.028 | 0.025 | |
| J. T. Dakin | 0.023 | 0.029 | 0.028 | 0.028 | 0.044 | |
| G. J. Feldman | 0.036 | 0.03 | 0.029 | 0.028 | 0.073 | |
| C. E. Friedberg | 0.031 | 0.028 | 0.028 | 0.028 | 0.029 | |
| D. Fryberger | 0.029 | 0.027 | 0.028 | 0.028 | 0.021 | |
| G. Goldhaber | 0.031 | 0.028 | 0.028 | 0.028 | 0.036 | |
| G. Hanson | 0.033 | 0.028 | 0.028 | 0.028 | 0.04 | |
| F. B. Heile | 0.019 | 0.026 | 0.027 | 0.028 | 0.002 | |
| B. Jean-Marie | 0.024 | 0.027 | 0.028 | 0.028 | 0.014 | |
| J. A. Kadyk | 0.031 | 0.028 | 0.028 | 0.028 | 0.029 | |
| R. R. Larsen | 0.031 | 0.028 | 0.028 | 0.028 | 0.033 | |
| A. M. Litke | 0.023 | 0.027 | 0.027 | 0.028 | 0.015 | |
| D. L ke | 0.027 | 0.027 | 0.027 | 0.028 | 0.023 | |
| B. A. Lulu | 0.019 | 0.027 | 0.027 | 0.028 | 0.008 | |
| V. L th | 0.03 | 0.028 | 0.028 | 0.028 | 0.027 | |
| D. Lyon | 0.021 | 0.027 | 0.027 | 0.028 | 0.008 | |
| C. C. Morehouse | 0.03 | 0.027 | 0.028 | 0.028 | 0.018 | |
| J. M. Paterson | 0.031 | 0.028 | 0.028 | 0.028 | 0.028 | |
| F. M. Pierre | 0.025 | 0.027 | 0.027 | 0.028 | 0.014 | |
| T. P. Pun | 0.026 | 0.028 | 0.027 | 0.028 | 0.024 | |
| P. A. Rapidis | 0.018 | 0.027 | 0.027 | 0.028 | 0.008 | |
| B. Richter | 0.036 | 0.03 | 0.028 | 0.028 | 0.075 | |
| B. Sadoulet | 0.027 | 0.027 | 0.027 | 0.028 | 0.019 | |
| R. F. Schwitters | 0.031 | 0.028 | 0.028 | 0.028 | 0.027 | |
| W. Tanenbaum | 0.027 | 0.027 | 0.027 | 0.028 | 0.021 | |
| G. H. Trilling | 0.031 | 0.028 | 0.028 | 0.028 | 0.029 | |
| F. Vannucci | 0.031 | 0.028 | 0.028 | 0.028 | 0.026 | |
| J. S. Whitaker | 0.027 | 0.027 | 0.028 | 0.028 | 0.02 | |
| F. C. Winkelmann | 0.019 | 0.027 | 0.027 | 0.028 | 0.006 | |
| J. E. Wiss | 0.026 | 0.027 | 0.027 | 0.028 | 0.017 |
Table S2. The credits of Nobel Prize-Winning papers identified by the algorithms (MAG dataset). All Nobel Prize winners in physics and their work owners have their scores bolded. |
| DOI | Author Name | CCA | NCCA | DCA | COCA | NCCAS |
|---|---|---|---|---|---|---|
| 10.1103/ PhysRevLett.76.1796 | D. M. Meekhof | 0.207 | 0.203 | 0.198 | 0.2 | 0.226 |
| C. Monroe | 0.258 | 0.203 | 0.201 | 0.263 | 0.357 | |
| B. E. King | 0.141 | 0.131 | 0.197 | 0.075 | 0.0 | |
| W. M. Itano | 0.152 | 0.154 | 0.198 | 0.106 | 0.041 | |
| D. J. Wineland | 0.254 | 0.254 | 0.204 | 0.356 | 0.376 | |
| 10.1103/ PhysRevLett.84.5102 | S. A. Diddams | 0.132 | 0.15 | 0.102 | - | 0.195 |
| D. J. Jones | 0.07 | 0.056 | 0.099 | - | 0.022 | |
| J. Ye | 0.123 | 0.126 | 0.102 | - | 0.17 | |
| S. T. Cundiff | 0.091 | 0.066 | 0.101 | - | 0.058 | |
| J. L. Hall | 0.127 | 0.147 | 0.1 | - | 0.185 | |
| J. K. Ranka | 0.062 | 0.05 | 0.098 | - | 0.0 | |
| R. S. Windeler | 0.065 | 0.05 | 0.098 | - | 0.003 | |
| R. Holzwarth | 0.117 | 0.139 | 0.1 | - | 0.15 | |
| T. Udem | 0.072 | 0.056 | 0.099 | - | 0.015 | |
| T. W. H nsch | 0.14 | 0.16 | 0.101 | - | 0.203 | |
| 10.1103/ PhysRevLett.77.4887 | M. Brune | 0.116 | 0.131 | 0.125 | 0.105 | 0.18 |
| E. Hagley | 0.116 | 0.118 | 0.125 | 0.012 | 0.001 | |
| J. Dreyer | 0.116 | 0.118 | 0.125 | 0.012 | 0.001 | |
| X. Ma tre | 0.116 | 0.118 | 0.125 | 0.012 | 0.001 | |
| A. Maali | 0.117 | 0.119 | 0.125 | 0.021 | 0.016 | |
| C. Wunderlich | 0.116 | 0.118 | 0.125 | 0.012 | 0.014 | |
| J. M. Raimond | 0.135 | 0.133 | 0.125 | 0.226 | 0.199 | |
| S. Haroche | 0.152 | 0.145 | 0.126 | 0.599 | 0.587 | |
| 10.1103/ PhysRevLett.55.48 | S. Chu | 0.3 | 0.34 | 0.211 | 0.527 | 0.786 |
| L. Hollberg | 0.173 | 0.162 | 0.197 | 0.153 | 0.037 | |
| J. E. Bjorkholm | 0.167 | 0.157 | 0.197 | 0.043 | 0.001 | |
| A. Cable | 0.181 | 0.178 | 0.198 | 0.116 | 0.112 | |
| A. Ashkin | 0.179 | 0.163 | 0.197 | 0.226 | 0.065 | |
| 10.1103/ PhysRevLett.61.2472 | M. N. Baibich | 0.107 | 0.104 | 0.111 | - | 0.043 |
| J. M. Broto | 0.104 | 0.098 | 0.111 | - | 0.0 | |
| A. Fert | 0.128 | 0.137 | 0.111 | - | 0.35 | |
| F. N. Van Dau | 0.107 | 0.104 | 0.111 | - | 0.045 | |
| F. Petroff | 0.126 | 0.138 | 0.111 | - | 0.337 | |
| P. Etienne | 0.111 | 0.112 | 0.111 | - | 0.117 | |
| G. Creuzet | 0.11 | 0.11 | 0.111 | - | 0.101 | |
| A. Friederich | 0.104 | 0.099 | 0.111 | - | 0.006 | |
| J. Chazelas | 0.104 | 0.098 | 0.111 | - | 0.0 | |
| 10.1103/ PhysRevLett.75.3969 | K. B. Davis | 0.106 | 0.09 | 0.142 | - | 0.0 |
| M. -O. Mewes | 0.122 | 0.113 | 0.142 | - | 0.056 | |
| M. R. Andrews | 0.151 | 0.152 | 0.142 | - | 0.184 | |
| N. J.vanDruten | 0.141 | 0.153 | 0.143 | - | 0.128 | |
| D. S. Durfee | 0.146 | 0.146 | 0.143 | - | 0.169 | |
| D. M. Kurn | 0.141 | 0.138 | 0.143 | - | 0.146 | |
| W. Ketterle | 0.192 | 0.209 | 0.144 | - | 0.317 | |
| 10.1103/ PhysRev.69.37 | E. M. Purcell | 0.414 | 0.461 | 0.342 | - | 0.614 |
| H. C. Torrey | 0.212 | 0.186 | 0.32 | - | 0.001 | |
| R. V. Pound | 0.374 | 0.353 | 0.338 | - | 0.384 | |
| 10.1103/ PhysRev.83.333 | C. G. Shull | 0.334 | 0.333 | 0.334 | - | 0.488 |
| W. A. Strauser | 0.333 | 0.333 | 0.333 | - | 0.256 | |
| E. O. Wollan | 0.333 | 0.333 | 0.333 | - | 0.256 | |
| 10.1103/ PhysRevLett.61.169 | P. D. Lett | 0.129 | 0.123 | 0.165 | 0.097 | 0.036 |
| R. N. Watts | 0.144 | 0.169 | 0.166 | 0.055 | 0.141 | |
| C. I. Westbrook | 0.127 | 0.113 | 0.165 | 0.081 | 0.01 | |
| W. D. Phillips | 0.282 | 0.277 | 0.17 | 0.288 | 0.521 | |
| P. L. Gould | 0.131 | 0.123 | 0.165 | 0.109 | 0.037 | |
| H. J. Metcalf | 0.186 | 0.195 | 0.168 | 0.371 | 0.255 | |
| 10.1103/ PhysRevLett.13.321 | F. Englert | 0.503 | 0.5 | 0.5 | - | 0.991 |
| R. Brout | 0.497 | 0.5 | 0.5 | - | 0.009 | |
| 10.1103/ PhysRev.122.345 | Y. Nambu | 0.506 | 0.507 | 0.5 | - | 0.996 |
| G. Jona-Lasinio | 0.494 | 0.493 | 0.5 | - | 0.004 | |
| 10.1103/ PhysRevLett.57.2442 | P. Gr nberg | 0.245 | 0.27 | 0.2 | - | 0.792 |
| R. Schreiber | 0.195 | 0.197 | 0.2 | - | 0.138 | |
| Y. Pang | 0.187 | 0.179 | 0.2 | - | 0.035 | |
| M. B. Brodsky | 0.185 | 0.176 | 0.2 | - | 0.0 | |
| H. Sowers | 0.187 | 0.179 | 0.2 | - | 0.035 | |
| 10.1103/ PhysRevLett.84.3232 | J. Reichert | 0.168 | 0.175 | 0.163 | - | 0.179 |
| M. Niering | 0.111 | 0.091 | 0.159 | - | 0.0 | |
| R. Holzwarth | 0.204 | 0.22 | 0.176 | - | 0.279 | |
| M. Weitz | 0.111 | 0.091 | 0.159 | - | 0.0 | |
| T. Udem | 0.176 | 0.184 | 0.163 | - | 0.198 | |
| T. W. H_nsch | 0.231 | 0.239 | 0.181 | - | 0.343 | |
| 10.1103/ PhysRevLett.20.1205 | R. Davis | 0.387 | 0.412 | 0.361 | - | 0.997 |
| D. S. Harmer | 0.306 | 0.294 | 0.32 | - | 0.002 | |
| K. C. Hoffman | 0.306 | 0.294 | 0.32 | - | 0.002 | |
| 10.1103/ PhysRevLett.48.1559 | D. C. Tsui | 0.325 | 0.326 | 0.333 | 0.213 | 0.281 |
| H. L. Stormer | 0.354 | 0.35 | 0.334 | 0.644 | 0.477 | |
| A. C. Gossard | 0.321 | 0.324 | 0.333 | 0.143 | 0.242 | |
| 10.1103/ PhysRevLett.61.826 | A. Aspect | 0.195 | 0.172 | 0.199 | - | 0.145 |
| E. Arimondo | 0.176 | 0.157 | 0.199 | - | 0.093 | |
| R. Kaiser | 0.154 | 0.138 | 0.198 | - | 0.021 | |
| N. Vansteenkiste | 0.151 | 0.132 | 0.198 | - | 0.0 | |
| C.Cohen-Tan | 0.324 | 0.401 | 0.208 | - | 0.74 | |
| 10.1103/ PhysRevLett.9.439 | R. Giacconi | 0.267 | 0.287 | 0.271 | - | 0.484 |
| H. Gursky | 0.264 | 0.285 | 0.243 | - | 0.454 | |
| F. R. Paolini | 0.233 | 0.212 | 0.243 | - | 0.001 | |
| B. B. Rossi | 0.236 | 0.215 | 0.243 | - | 0.061 | |
| 10.1103/ PhysRev.72.241 | W. E. Lamb | 0.516 | 0.502 | 0.504 | 0.75 | 0.835 |
| R. C. Retherford | 0.484 | 0.498 | 0.496 | 0.25 | 0.165 | |
| 10.1103/ PhysRev.73.679 | N. Bloembergen | 0.331 | 0.329 | 0.333 | - | 0.363 |
| E. M. Purcell | 0.344 | 0.356 | 0.333 | - | 0.524 | |
| R. V. Pound | 0.325 | 0.316 | 0.333 | - | 0.113 | |
| 10.1103/ PhysRevLett.58.1490 | K. Hirata | 0.044 | 0.044 | 0.044 | - | 0.055 |
| T. Kajita | 0.043 | 0.043 | 0.043 | - | 0.048 | |
| M. Koshiba | 0.043 | 0.043 | 0.043 | - | 0.048 | |
| M. Nakahata | 0.043 | 0.043 | 0.043 | - | 0.044 | |
| Y. Oyama | 0.043 | 0.043 | 0.043 | - | 0.074 | |
| N. Sato | 0.043 | 0.043 | 0.043 | - | 0.041 | |
| A. Suzuki | 0.043 | 0.043 | 0.043 | - | 0.022 | |
| M. Takita | 0.043 | 0.043 | 0.043 | - | 0.048 | |
| Y. Totsuka | 0.043 | 0.043 | 0.043 | - | 0.074 | |
| T. Kifune | 0.044 | 0.044 | 0.044 | - | 0.055 | |
| T. Suda | 0.043 | 0.043 | 0.043 | - | 0.044 | |
| K. Takahashi | 0.044 | 0.044 | 0.044 | - | 0.005 | |
| T. Tanimori | 0.043 | 0.043 | 0.043 | - | 0.032 | |
| K. Miyano | 0.043 | 0.043 | 0.043 | - | 0.074 | |
| M. Yamada | 0.043 | 0.043 | 0.043 | - | 0.029 | |
| E. W. Beier | 0.044 | 0.044 | 0.044 | - | 0.035 | |
| L. R. Feldscher | 0.043 | 0.043 | 0.043 | - | 0.022 | |
| S. B. Kim | 0.043 | 0.043 | 0.043 | - | 0.074 | |
| A. K. Mann | 0.043 | 0.043 | 0.043 | - | 0.074 | |
| F. M. Newcomer | 0.044 | 0.044 | 0.044 | - | 0.074 | |
| R. Van | 0.043 | 0.043 | 0.043 | - | 0.055 | |
| W. Zhang | 0.043 | 0.043 | 0.043 | - | 0.07 | |
| B. G. Cortez | 0.043 | 0.043 | 0.043 | - | 0.022 | |
| 10.1103/ PhysRevD.5.528 | G. Miller | 0.076 | 0.077 | 0.077 | - | 0.035 |
| E. D. Bloom | 0.076 | 0.077 | 0.077 | - | 0.035 | |
| G. Buschhorn | 0.076 | 0.077 | 0.077 | - | 0.035 | |
| D. H. Coward | 0.076 | 0.077 | 0.077 | - | 0.035 | |
| H. DeStaebler | 0.076 | 0.077 | 0.077 | - | 0.035 | |
| J. Drees | 0.076 | 0.077 | 0.077 | - | 0.035 | |
| C. L. Jordan | 0.076 | 0.077 | 0.077 | - | 0.035 | |
| L. W. Mo | 0.076 | 0.077 | 0.077 | - | 0.035 | |
| R. E. Taylor | 0.076 | 0.077 | 0.077 | - | 0.035 | |
| J. I. Friedman | 0.079 | 0.078 | 0.079 | - | 0.305 | |
| G. C. Hartmann | 0.076 | 0.077 | 0.077 | - | 0.035 | |
| H. W. Kendall | 0.079 | 0.078 | 0.079 | - | 0.305 | |
| R. Verdier | 0.076 | 0.077 | 0.077 | - | 0.035 | |
| 10.1103/ PhysRevLett.35.1489 | M. L. Perl | 0.025 | 0.015 | 0.013 | - | 0.214 |
| G. S. Abrams | 0.014 | 0.014 | 0.014 | - | 0.022 | |
| A. M. Boyarski | 0.014 | 0.014 | 0.013 | - | 0.006 | |
| M. Breidenbach | 0.013 | 0.013 | 0.014 | - | 0.022 | |
| D. D. Briggs | 0.014 | 0.014 | 0.014 | - | 0.0 | |
| F. Bulos | 0.013 | 0.013 | 0.013 | - | 0.0 | |
| W. Chinowsky | 0.013 | 0.013 | 0.013 | - | 0.006 | |
| J. T. Dakin | 0.013 | 0.013 | 0.013 | - | 0.0 | |
| G. J. Feldman | 0.014 | 0.014 | 0.014 | - | 0.016 | |
| C. E. Friedberg | 0.014 | 0.014 | 0.014 | - | 0.0 | |
| D. Fryberger | 0.013 | 0.013 | 0.014 | - | 0.0 | |
| G. Goldhaber | 0.014 | 0.014 | 0.014 | - | 0.022 | |
| G. Hanson | 0.013 | 0.013 | 0.013 | - | 0.022 | |
| F. B. Heile | 0.013 | 0.013 | 0.014 | - | 0.002 | |
| B. Jean-Marie | 0.014 | 0.014 | 0.014 | - | 0.0 | |
| J. A. Kadyk | 0.013 | 0.013 | 0.013 | - | 0.022 | |
| R. R. Larsen | 0.013 | 0.013 | 0.013 | - | 0.0 | |
| A. M. Litke | 0.013 | 0.013 | 0.013 | - | 0.007 | |
| D. L ke | 0.013 | 0.013 | 0.013 | - | 0.022 | |
| B. A. Lulu | 0.014 | 0.014 | 0.014 | - | 0.0 | |
| V. L th | 0.013 | 0.013 | 0.013 | - | 0.006 | |
| D. Lyon | 0.013 | 0.013 | 0.013 | - | 0.0 | |
| C. C. Morehouse | 0.013 | 0.013 | 0.013 | - | 0.0 | |
| J. M. Paterson | 0.013 | 0.013 | 0.014 | - | 0.022 | |
| F. M. Pierre | 0.014 | 0.014 | 0.014 | - | 0.0 | |
| T. P. Pun | 0.013 | 0.014 | 0.014 | - | 0.022 | |
| P. A. Rapidis | 0.013 | 0.013 | 0.013 | - | 0.022 | |
| B. Richter | 0.013 | 0.013 | 0.013 | - | 0.006 | |
| B. Sadoulet | 0.013 | 0.013 | 0.013 | - | 0.0 | |
| R. F. Schwitters | 0.013 | 0.013 | 0.014 | - | 0.0 | |
| W. Tanenbaum | 0.013 | 0.014 | 0.014 | - | 0.006 | |
| G. H. Trilling | 0.013 | 0.013 | 0.013 | - | 0.0 | |
| F. Vannucci | 0.014 | 0.014 | 0.014 | - | 0.0 | |
| J. S. Whitaker | 0.013 | 0.013 | 0.014 | - | 0.0 | |
| F. C. Winkelmann | 0.013 | 0.013 | 0.013 | - | 0.0 | |
| J. E. Wiss | 0.013 | 0.013 | 0.013 | - | 0.022 |
Figure S1. The distribution of Δ by different methods for papers published in different years. |
Figure S2. The distribution of the number of added papers by different methods for papers published in different years. |
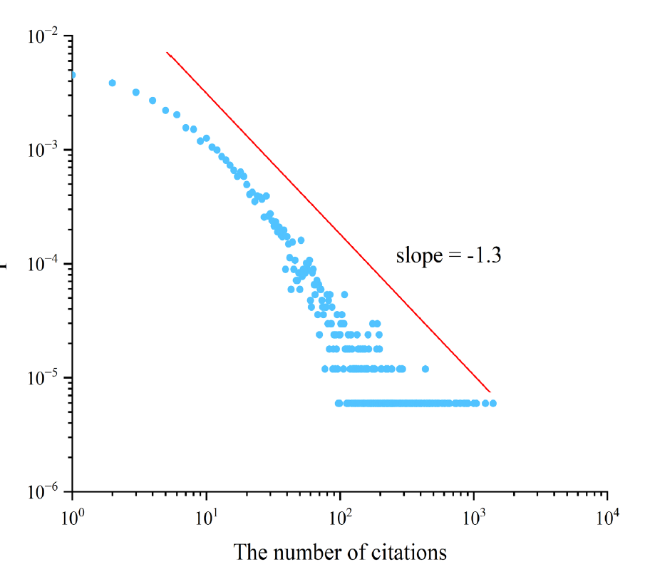
Figure S3. The citation distribution of citing papers related to Nobel Prize-winning papers. |