1 Introduction
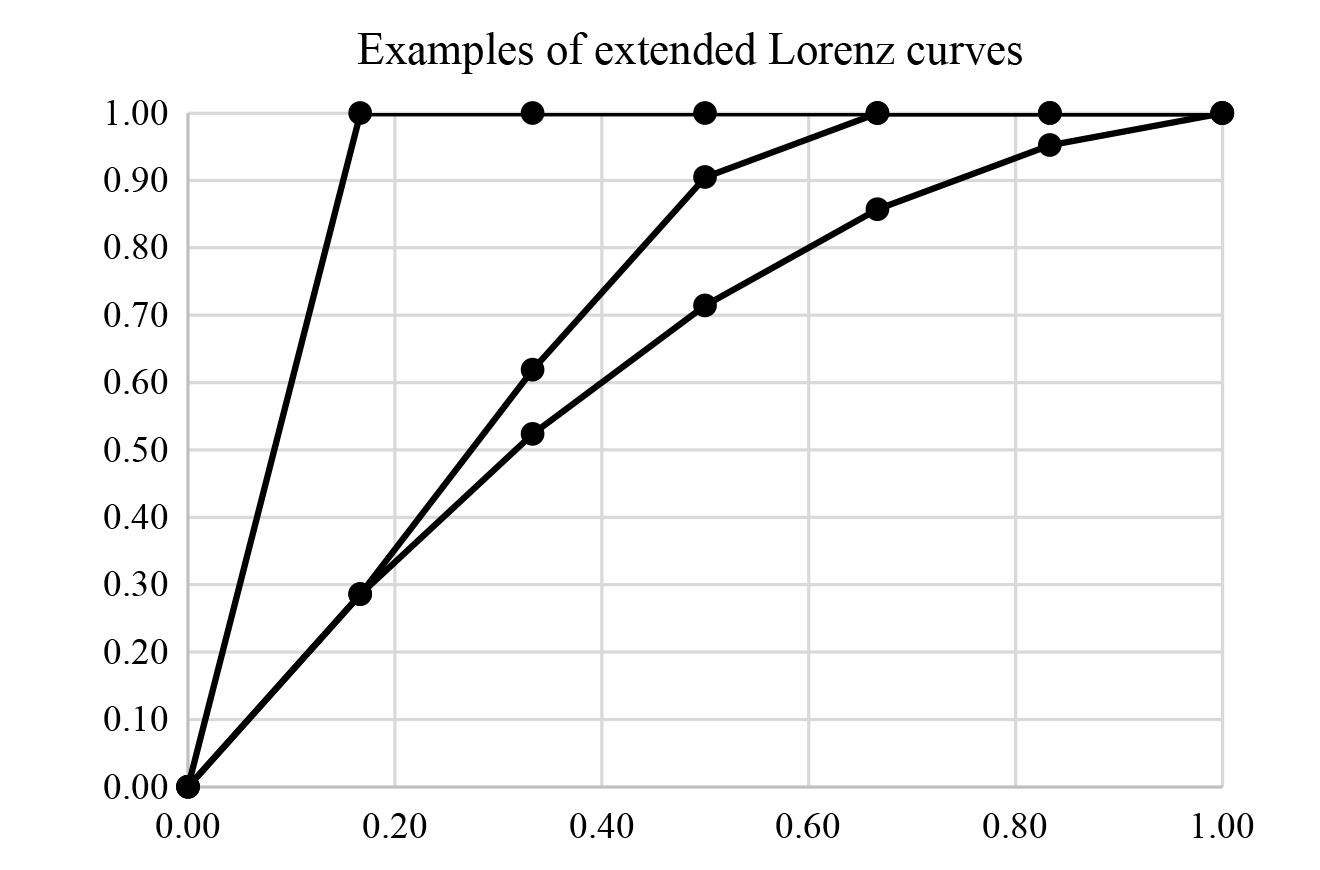
Figure 3. Extended Lorenz curves of K7, G0 and C6 (the chain of length 6). |
2 The main result
3 Remarks and consequences
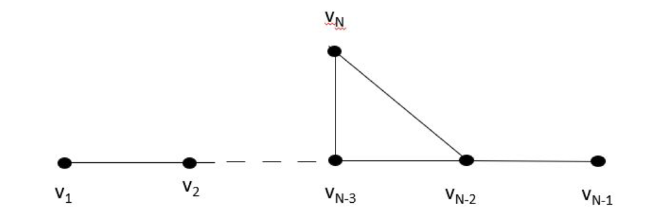
Figure 1. An example of a network for which $\forall i=1, \ldots, N-1: \alpha_{i}<\beta_{i}$. |
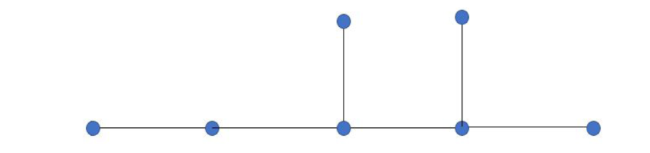
Figure 2. An example of a network, G0, with seven nodes. |