1 Introduction
In the era of mobile internet, internet giants have been investing huge amounts of money to support content generation. This attracts folk forces to produce a large number of high-quality and professional content. Labeling the Internet is a lifesaver for the explosion of content, which enables massive amounts of content to be organized, managed, and discovered effectively. A piece of content doesn’t always belong to one category but may be attached with multiple labels. The labels can be seen as a more specific and more dimensional classification system.
In the field of scientometrics and informetrics, similar phenomena can also be observed. Many science, technology and innovation (STI) resources are attached with several different labels, such as IPC (International Patent Classification) and CPC (Cooperative Patent Classification) for patent documents, and PACS (Physics and Astronomy Classification Scheme) numbers for scientific publications. In machine learning language, it is referred to as a multi-label classification problem (Chen et al., 2022; Xu & An, 2019).
Unlike binary classification and multi-class classification, multi-label classification aims to solve the problem of assigning a subset of labels to a given instance. That is to say, a particular instance can be assigned more than one label. Compared with other classification problems, the main characteristics of many multi-label classification tasks are two-fold (Deerwester et al., 1990; Pang & Lee, 2008; Xu & An, 2019): (1) the number of labels is large and their distribution is skewed, which results in exponential output space; (2) there exists some underlying label correlations, such as hierarchy structure between labels.
There are many open-source multi-label classification tools, which are deemed by their resulting authors to perform well on benchmark datasets, such as Yahoo (Ueda & Saito, 2002), RCV1-V2 (Lewis et al., 2004), Yeast (Elisseeff & Weston, 2001), etc. However, the creation time of these benchmark datasets is somewhat dated, and the characteristics of real-world multi-label datasets are not completely in line with those of benchmark ones (cf. Subsection Dataset’s Characteristics). Therefore, how to choose appropriate methods and tools in the face of large-scale multi-label classification problems is the main purpose of this paper. To exploit the applicability and power, this paper takes seven representative approaches into consideration: dependency-LDA (Rubin et al., 2012), MLkNN (Zhang & Zhou, 2007), LabelPowerset (Tsoumakas & Vlahavas, 2007), RAkEL (Tsoumakas et al., 2011), TextCNN (Kim, 2014), TexRNN (Liu et al., 2016), and TextRCNN (Lai et al., 2015).
The rest of the article is organized as follows. After Section Related Work briefly describes the mainstream algorithms for multi-label classification, seven approaches are introduced in Section Methodologies. Then, three real-world multi-label datasets are constructed in Section Datasets, and the dataset’s characteristics and the strategy for splitting training and test sets are also introduced in this section. Finally, on the basis of extensive comparative experiments in Section Results and Discussion, Section Conclusions concludes this study.
2 Related work
Madjarov et al. (2012) categorized the existing multi-label classification methods into three families: problem transformation, algorithm adaptation and ensemble. In the following subsections, we will review each of these three types of methods in detail.
2.1 Problem transformation methods
The problem transformation methods aim to tackle problems by converting multi-label classification problem to one or more single-label problems. Binary Relevance (BR) (Li & Ogihara, 2003) and ClassifierChain (CC) (Read et al., 2011) are two popular methods that transform multi-label classification problems into single-label binary classification problems. However, the BR strategy and CC strategy fail to utilize the correlations between labels. The Label Powerset methodology (Tsoumakas & Vlahavas, 2007) treats each distinct label combination as a separate class, leading to a multi-class classification task. This approach generates an extensive range of possible label combinations.
2.2 Algorithm adaptation methods
The algorithm adaptation methods aim to transform single-label classification algorithms to accommodate multi-label data. Typically, Clare & King (2001) proposed using the concept of information gain, which was inspired by decision trees, to select features and generate classifiers. The Multi-Label k-Nearest Neighbor Algorithm (MLkNN) (Zhang & Zhou, 2007) begins by searching for the k-Nearest examples and subsequently calculating distances to make the final decision on labels. Adaboost.MH and Adaboost.MR (Schapire, 1999) uses an iterative approach to update the estimated sample weights using a weak classifier and determine the final predicted labels through weighted voting. Rank-SVM (Elisseeff & Weston, 2001) and Multi-Label Least-Squares Support Vector Machine (ML2S-SVM) (Xu & An, 2019) are based on the principles of support vector machines and incorporate kernel tricks to effectively handle multi-label classification problems. It is worth noting that the advancement of deep learning techniques in recent years has led to the emergence of several promising deep learning-based methods for multi-learning, including ML-Net (Du et al., 2019), PatentNet (Haghighian Roudsari et al., 2022) and so on.
2.3 Ensemble methods
Ensemble methods strive to enhance the performance of classifiers by employing a combination of strategies, examples of such methods include ensemble classifier chains (ECC), ensemble random K-label sets (RAkEL), and ensemble of neural network-based algorithms. The resulting representations derived from the ensemble methodology have demonstrated a marked propensity to enhance the accuracy and resilience of multi-label classification models.
ECC represents a technique that involves a series of classifiers (CC) (Freitas Rocha et al., 2022) in selecting the optimal label through an aggregation of votes for each label. Meanwhile, the integration of neural network-based algorithms aims to amalgamate various deep learning techniques to resolve the problem of multi-label topic classification. On the other hand, RakEL (Tsoumakas et al., 2010) uses a set of LabelPowerset classifiers, where each set of k-labels is trained as a multi-label classifier. During the prediction phase, the algorithm integrates a voting mechanism to combine the prediction results from multiple classifiers.
2.4 Open-source toolkits
To the best of our knowledge, several open-source toolkits, implementing the above multi-label classification learning methods, can be accessed freely (see Table 1 for details). Though it is still unknown the performance on real-world datasets until now. Therefore, three of these toolkits are chosen to conduct comprehensive comparative analysis: Dependency-LDA (Rubin et al., 2012), Scikit-Multilearn (Szymanski & Kajdanowicz, 2017) and Neural Classifier (Liu et al., 2019). Apart from Dependency-LDA, both Scikit-Multilearn and Neural Classifier implement a suit of multi-label classification approaches.
Table 1. Several open-source toolkits for solving multi-label classification problems. |
| Name | Link |
|---|---|
| Dependency LDA | https://github.com/timothyrubin/DependencyLDA |
| Scikit-Multilearn | http://scikit.ml/index.html |
| Magpie | https://github.com/inspirehep/magpie |
| Hierarchical Text Multi Label Classification | https://github.com/RunlongYu/Hierarchical-Text-Multi-Label-Classificaiton |
| Keras-TextClassification | https://github.com/yongzhuo/Keras-TextClassification |
| Neural Classifier | https://github.com/Tencent/NeuralNLP-NeuralClassifier |
The Scikit-Multilearn is a Python library, which encapsulates eleven multi-label classification learning methods. For the sake of comprehensiveness, this article chooses a representative from each type described above as follows: LabelPowerset, MLkNN, and RakEL. The Neural Classifier is a text classification toolbox on the basis of the deep learning framework PyTorch. This toolbox implements a variety of deep learning methods, which can not only consider the dependency between the labels, but also the hierarchical structure of the labels in the format of tree or Directed Acyclic Graph (DAG). It has been shown that the TextCNN, TexRNN and TextRCNN perform better than other algorithms (Liu et al., 2019).
3 Methodologies
In this study, the following seven multi-label classification methods are chosen for performance comparison: Dependency-LDA, LabelPowerset, RAkEL, MLkNN, TextCNN, TexRNN, and TextRCNN. The main reasons for choosing these methods are three-fold as follows. (1) All three types of approaches (cf. Section Related Work) should be covered. (2) To benefit from the cutting-edge deep learning techniques, deep learning models are preferred here. (3) The resulting approach should scale to the large-scale dataset.
For the sake of clarity for the readers, the following subsection describes briefly these seven methods one by one. For more elaborate and detailed descriptions, we refer the readers to their original papers.
3.1 Dependency-LDA model
The Dependency-LDA model (Rubin et al., 2012) is a kind of probabilistic topic models, which derives from Latent Dirichlet Allocation (LDA) model (Blei et al., 2003). This model is able to capture the dependencies between the labels as well as the prior label frequencies. It significantly improves performance over the Flat-LDA and Prior-LDA models (Rubin et al., 2012), and is highly competitive with popular discriminative approaches on large-scale datasets. It is worth mentioning that the Dependency-LDA model has a strong performance advantage when the distribution of label frequencies is highly skewed.
In a multi-label classification task, the labels are available at the training phrase. But it is more complex to infer the best label set for a document without any label since each label assignment is evaluated in the first place and then the ones with top highest posterior probability are returned. This model allows us to explore the entire topic space of each document with all possible label assignments. By setting an appropriate threshold for the posterior probability of the topic, one can infer the most likely label set for an interested document.
3.2 MLkNN method
The MLkNN method (Zhang & Zhou, 2007), as a representative of algorithm adaptation methods, is developed from the traditional k-Nearest Neighbor (kNN) approach. The main idea of MLkNN method is that, for each test sample, its k-nearest neighbors (the k instances with the smallest distance from it in the feature space) are found from the training set in the first place. Then, the statistical information of these neighbors, such as the number of neighbors belonging to the same category and the maximum posteriori probability principle (MAP), is used to determine the label set of a focal test sample.
3.3 Label powerset method
the Label Powerset (LP) (Tsoumakas & Vlahavas, 2007) transforms a multi-label classification problem into a multi-class classification problem. This method maps each unique label combination to a new category, and then a multi-class classification method can be readily utilized. In this way, the relationship between the labels can be fully taken into account, while simplifying the problem.
For ease of understanding, let’s take Figure 1 as an example. In this case, the instance E1 is attached to the labels y2 and y3. One can create a new label y2,3 to denote the combination of y2 and y3. Thus, the problem of assigning the combinations of {y1, y2, y3, y4} to the resulting instances is transformed into the problem of dividing the instances into four categories: {y1, y2,3, y3,4, y1,3}. It avoids, to some extent, the problem of an exponential increase in the label space when dealing with all label combinations.
Figure 1. An example of the Mechanism of LP Algorithm. |
3.4 RAkEL method
The RAkEL method (Tsoumakas et al., 2011) is actually an ensemble of Label Powerset (LP) classifiers (Tsoumakas & Vlahavas, 2007), in which each LP classifier is trained on a different small random subset of labels. Compared to the LP method, the RAkEL method can consider the label correlations, and avoid the problem of high complexity to some extent.
In more detail, the RAkEL method iteratively constructs an ensemble of m LP classifiers. At each iteration, it randomly selects a k-labelset (viz. the label combination with k elements) from the space of possible label combinations without replacement. Then, an LP classifier is trained on the chosen k-labelset. Note that the number of iterations and the size of the labelsets k are two core parameters preset by users. Finally, the predicted results of LP classifiers are counted and the label set of a target instance can be obtained according to a threshold (0.5 in general).
It’s worth mentioning that two variants are proposed by Szymanski et al. (2016): (1) the RAkELd method divides the label set into k disjoint subsets, and (2) the RAkELo allows overlapping of label subspaces. In this study, the RAkELd method is utilized in the following experiments. Since the labels of the three datasets in this study (cf. Section Dataset) have a certain hierarchical relationship, we should follow the principle of “mutual exclusion” in the division of the label sets, so the former is chosen here.
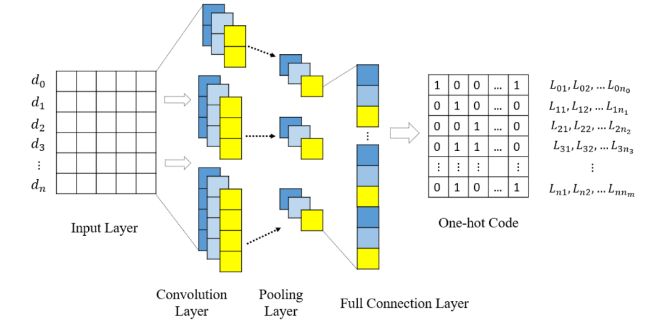
3.5 TextCNN model
The TextCNN model (Kim, 2014), shown in Figure 2 , consists of four parts: input layer, convolution layer, pooling layer and full connection layer. It processes fixed-length text sequences, using word embeddings for representation. Texts are adjusted to a specified length by either filling in short sequences or truncating longer ones. The sentences from the first layer can be expressed as cohesive operator expressions of word tokens. These sentences then slide in one dimension within a certain height (window value) of the convolution kernel to generate the new feature ci by setting a filter w, ci is calculated by the formula ci=f(w⋅xi:i+h-1+b), where xi:j represents the connection of words xi, xi+1, …, xi+j, b is a bias term and f is a nonlinear function.
Figure 2. The graph model representation of the TextCNN Model. |
The convolution layer outputs a feature graph, which is then processed by max-pooling in the pooling layer to produce a fixed-length output. This output feeds into a full connection layer, culminating in a Logistic Regression classifier that outputs label probabilities.
3.6 TextRNN model
As the name states, the TextRNN model (Liu et al., 2016) has a capacity for short-term memory. The inputs to the model are related not only to the input at the present moment, but also to its output over a period of time. As a matter of fact, the TextRNN model is an extension of the traditional feed-forward neural network for text classification because its recursive structure is well suited for processing variable-length sentence inputs.
It dynamically updates the hidden layer based on both the immediate input and feedback from previous states, utilizing a nonlinear function to process sequences. This model learns the correlation between sequential inputs and outputs, with past outputs significantly influencing future ones. It emphasizes the importance of label frequency in training, arranging labels in descending order of occurrence for effective label correlation learning. The final output represents the sequence, feeding into layers that predict label probabilities. Parameters are minimized against cross entropy to accurately classify instances. Similar to the TextCNN, the TextRNN employs word embedding in its input layer, transitioning from sparse one-hot vectors to dense word vectors.
3.7 TextRCNN model
The recursive convolutional neural network (RCNN) (Lai et al., 2015) can introduce less noise and capture the context information to the maximum extent when learning the word representation. In addition, the model can retain a larger range of word ordering when learning textual representation. The RCNN model combines the advantages of RNN and CNN, and introduces the idea of RNN based on the four-part structure of CNN (Lai et al., 2015). It processes documents as sequences of words, aiming to classify them into resulting labels based on the probability p(k|D,θ), where θ represents the network parameters. The RCNN uniquely constructs word representations by combining context from both sides of a word with the word itself, utilizing bidirectional RNNs for context extraction. Context vectors cl(wi) and cr(wi) for each word are generated through specific equations, incorporating word embeddings and shared parameters for sentence boundaries to create a comprehensive representation of each word.
4 Datasets
To evaluate the performance of seven multi-label classification approaches, three real-world datasets from SciGraph and USPTO database are used here. The SciGraph integrates most of Springer Nature’s journals, conference papers, and academic monographs, as well as other online resources such as DBpedia and Wikipedia. Each journal paper in the SciGraph often involves multiple disciplines and topics, so it is assigned multiple SciGraph discipline classification numbers. We select all journal publications from 2011 to 2017 under two branches of classification system: Health-Sciences and Biological-Sciences. After eliminating scholarly articles with missing information (such as no label information or no abstract, and so on), the Health-Sciences branch contains 21,168 papers with 507 unique labels, and the Biological-Sciences branch has 11,292 papers with 484 unique labels. As for the USPTO dataset, this study extracts all patents with publication year 2019. In total, there are 355,530 patents. The 8-character CPC codes are viewed as the labels of each patent document in order to avoid the exponential growth of label space. In the end, 9,519 unique CPC labels are obtained in this work.
4.1 Dataset’s characteristics
To demonstrate the difficulty of multi-label classification on the real-world datasets, Table 2 reports the characteristics of our datasets and several benchmark ones: emotions (Trohidis et al., 2011), scene (Boutell et al., 2004), bibtex (Katakis et al., 2008), and medical (Pestian et al., 2007). From Table 2 , several phenomena can be observed as follows. (a) The number of instances and labels in the benchmark datasets is much less than that in our datasets. (b) The labels in our datasets show a clear hierarchical structure, but no hierarchical structure is observed from the benchmark datasets. Among our three datasets, the Biological-Sciences dataset ranks first in terms of the number of hierarchies, followed by the Health-Sciences dataset. (c) The label output space of our datasets, especially USPTO dataset, is generally larger than that of the benchmark datasets in terms of label cardinality. The label cardinality represents the average number of labels allocated to an instance. (d) Our datasets are more unbalanced than the benchmark datasets in terms of the number of documents per label (cf. the last three columns in Table 2 ). Among our three datasets, the number of documents allocated to each label varies the most in the USPTO dataset, followed by the Health-Science dataset. Notably, due to the limited instances within the sub-group levels of IPC and CPC, this study has limited the hierarchy to the group level.
Table 2. Characteristics of our datasets and benchmark datasets. |
| Dataset | #of instances | #of labels | #of hierarchies | Label cardinality | doc/label | ||
|---|---|---|---|---|---|---|---|
| Avg. | Max. | Min. | |||||
| Health-Sciences | 21,168 | 507 | 5 | 2.25 | 94.10 | 1,571 | 1 |
| Biological-Sciences | 11,292 | 484 | 6 | 1.56 | 36.29 | 606 | 1 |
| USPTO | 355,058 | 8,867 | 4 | 4.08 | 152.38 | 20,988 | 1 |
| Emotions | 593 | 6 | 1 | 1.869 | 184.67 | 264 | 148 |
| Scene | 2,407 | 6 | 1 | 1.074 | 430.83 | 533 | 364 |
| Bibtex | 7,395 | 159 | 1 | 2.401 | 112 | 1,042 | 51 |
| Medical | 978 | 45 | 1 | 1.25 | 27 | 266 | 1 |
To understand intuitively the highly skewed distribution of label frequencies, Figure 3 illustrates the power-law distribution characteristics of our three datasets. From Figure 3 , it is not difficult to see that the vast majority of the labels are associated with a small number of documents, and relatively few labels are assigned to a large number of documents. This is a very popular characteristic in the real-world multi-label classification problems (Dekel & Shamir, 2010; Liu et al., 2005; Yang et al., 2003).
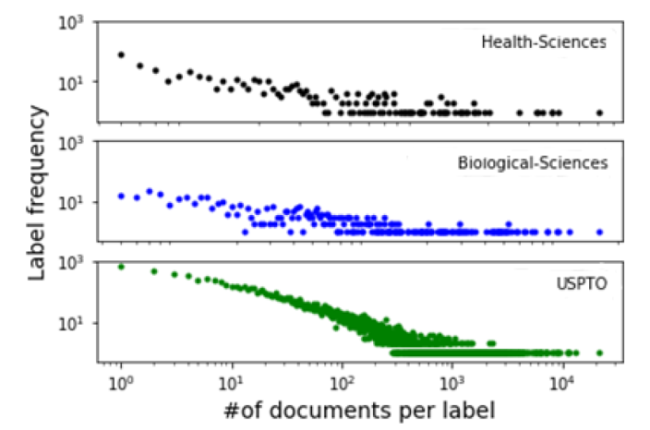
Figure 3. Power-law distribution of the three datasets. |
In addition, this part uses NLTK tools in Python to process text, including sentence and word segmentation, part-of-speech tagging, word-type reduction, deactivation and removal of stop words, punctuation marks and numbers. After these pre-processing steps, our datasets mainly consist of semantic word stems. In the end, the statistics of each dataset are shown in Table 3 .
Table 3. The number of word tokens and unique words in our datasets. |
| Datasets | #of word tokens | #of unique words |
|---|---|---|
| Health-Sciences | 1,556,854 | 64,113 |
| Biological-Sciences | 1,486,840 | 45,610 |
| USPTO | 2,540,118 | 81,268 |
4.2 Training and test sets
Since an instance is attached with multiple labels, it is not trivial to group a multi-label dataset into two disjoint subsets. Before splitting our dataset into training and test sets, we identify the following rules. (1) An instance does not belong to two sets at the same time. To say it in another way, the training set has no intersection with the test set. (2) The label set in the test set is a subset of the label set in the training set. That is to say, each label must appear in the training set, and several labels are allowed not to appear in the test set. (3) In our experiment, the ratio between the number of instances in the training and test set is approximately 4:1.
To enable our splitting procedure to follow the above rules, the stratification method in Sechidis et al. (2011) is utilized in the first place. Then, we manually adjust several instances that do not meet the above requirements. In the end, the number of instances in the training set and test set is shown in Table 4 .
Table 4. The number of instances in the training and test sets of our datasets. |
| Datasets | Training Set | Test Set |
|---|---|---|
| Health-Sciences | 16,932 | 4,236 |
| Biological-Sciences | 9,034 | 2,258 |
| USPTO | 283,899 | 71,622 |
5 Experimental results and discussions
5.1 Evaluation measures
In the literature, two groups of measures are usually utilized: the label-based evaluation measures and the instance-based evaluation measures. As for the former, the performance of a single label in all instances is calculated in terms of accuracy, precision, recall and F1 score, and then one averages the performance of all labels to obtain an overall performance (Tsoumakas & Vlahavas, 2007). The latter is further divided into classification-based measures and ranking-based measures (Ghamrawi & Mccallum, 2005; Godbole & Sarawagi, 2004).
Generally speaking, there are no universal multi-label classification evaluation measures for all problems. In this study, the following three classification-based measures are adopted: Macro-F1, Micro-F1 and Hamming Loss.
(1) Macro-F1: One can obtain the F1 score for each label after the precision and recall are calculated on the basis of true positives (TP), false negatives (FN), and false positives (FP) [cf. Eq. (1) - (3)]. The macro-F1 is defined as the average of the F1 scores for all labels [cf. Eq. (4)].
precisioni = TPi/(TPi +FPi)
recalli = TPi/(TPi+FNi)
F1i=2×precisioni×recalli/(precisioni+recalli)
Macro F1=∑1LF1i/L
(2) Micro-F1: After counting and summing the true positives, false negatives, and false positives of each label [cf. Eq. (5) - (7)], micro-F1 score can be calculated on the basis of precision and recall [cf. Eq. (8) - (10)]. It is easy to see that this measure does not take into account the imbalance of labels.
TP=∑1LTPi
FP=∑1LFPi
FN=∑1LFNi
precision=TP/(TP+FP)
recall=TP/(TP+FN)
Micro F1=2× precision×recall/(precision+recall)
(3) Hamming Loss: This measure represents the proportion of error samples in all labels [cf. Eq. (11)]., The smaller the value of Hamming loss, the better the method.
Hloss=∑1L|f(Xi)∆Yi|/n
Here, “∆” denotes the symmetric difference between the ground-truth label set and the predicted one, f(Xi) represents the predicted set of labels for the i-th sample, and Yi denotes the ground-truth label set of labels for that sample.
5.2 Performance comparison
Each method has several core parameters. It is well-documented that these parameters will influence the performance of the resulting method. Therefore, it is necessary to tune the core parameters of each approach before performance comparison.
The majority of the experiments conducted within this study are executed on Colab servers, which are equipped with a GPU of 16GB and a CPU of 12GB, resulting in approximate program execution times of around 2 hours. For deep learning models, such as RCNN, and for processing larger datasets, such as USPTO, the most substantial server configurations utilized comprise a GPU of 48GB and a CPU of 64GB, with program run times approximating 10 hours.
5.2.1 Dependency-LDA model
According to Rubin et al. (Rubin et al., 2012), the parameters η and βW are generally insensitive to the performance as long as η≫1 and βW≪ 1. Hence, this study fixed η and βW to 50 and 0.01, respectively. In the dependency-LDA model, one of the most important parameters is the number of topics (T). Rubin et al. (2012) suggested that the number of topics (T) should be approximately equal to the number of unique labels (C) for small datasets. However, when T≪C, the interpretability of themes from this model will be greatly improved, and the model complexity is also able to be controlled properly. Therefore, this work sets T∈{20,50,100} for the Biological-Sciences and Health-Sciences datasets and T∈{50,100,200,400} for the USPTO dataset.
Another core parameter in the dependency-LDA model is the pseudo-count βC. In this work, this parameter is set to be approximately equal to one-tenth of the total count contributed by the observed labels. Formally, this parameter can be expressed as Eq. (12).
T∙Cunique∙βC≈Ctotal/10
Thus, the parameter βC corresponding to different numbers of topics can be fixed to 0.18, 0.07, and 0.04 for the Biological-Sciences dataset, 0.47, 0.19, and 0.09 for the Health-Sciences dataset, and 0.40, 0.20, 0.10, and 0.05 for the USPTO dataset.
Table 5. Performance of the dependency-LDA model with different parameter settings on three real-world datasets. |
| Dataset | #of topics | βC | Macro F1 | Micro F1 | Hamming loss |
|---|---|---|---|---|---|
| Biological- Sciences | 20 | 0.18 | 0.0443 | 0.0101 | 0.2537 |
| 50 | 0.07 | 0.0438 | 0.0102 | 0.2540 | |
| 100 | 0.04 | 0.0436 | 0.0096 | 0.2544 | |
| Health-Sciences | 20 | 0.47 | 0.0412 | 0.0100 | 0.2542 |
| 50 | 0.19 | 0.0410 | 0.0102 | 0.2590 | |
| 100 | 0.09 | 0.0386 | 0.0102 | 0.2603 | |
| USPTO | 50 | 0.40 | 0.0023 | 0.0010 | 0.1274 |
| 100 | 0.20 | 0.0022 | 0.0012 | 0.1316 | |
| 200 | 0.10 | 0.0022 | 0.0012 | 0.1343 | |
| 400 | 0.05 | 0.0026 | 0.0010 | 0.0895 |
5.2.2 MLkNN, RAkEL, and LaberPowerset
This study utilizes the implementation of these three methods in the Scikit-Multilearn (Szymanski & Kajdanowicz, 2017). By trial and error, the number of nearest neighbors (K) and the smoothing parameter (S) in the MLkNN method are fixed to 2 and 0.5 respectively. In the RAkEL method, base classifier and the expected size of each partition (labelset_size) assume respectively Gaussian Naïve Bayes (Xu, 2018) and 4. As for the LabelPowerset method, this study takes Random Forest as a base classifier, and the number of estimators (n_estimators) is fixed to 100. A common core parameter in these three approaches is the maximum number of features. According to our observation, it is better that this parameter is consistent with the size of vocabulary in each dataset. Therefore, 800 and 1,000 are attached to this parameter for the Biological-Sciences and Health-Sciences datasets, and 12,000 and 18,000 for the USPTO dataset.
Table 6. Performance of the MLkNN, RAkEL, and LabelPowerset methods with different parameter settings on three real-world datasets. |
| Dataset | Method | Max-features | Macro F1 | Micro F1 | Hamming Loss |
|---|---|---|---|---|---|
| Biological-Sciences | MLkNN | 800 | 0.0831 | 0.1535 | 0.3389 |
| 1,000 | 0.0836 | 0.1532 | 0.3404 | ||
| RAkEL | 800 | 0.0280 | 0.0794 | 0.2859 | |
| 1,000 | 0.0229 | 0.0637 | 0.2923 | ||
| LabelPowerset | 800 | 0.0044 | 0.0219 | 0.3845 | |
| 1,000 | 0.0042 | 0.0195 | 0.3850 | ||
| Health-Sciences | MLkNN | 800 | 0.0738 | 0.1364 | 0.2727 |
| 1,000 | 0.0806 | 0.1242 | 0.2759 | ||
| RAkEL | 800 | 0.0284 | 0.0858 | 0.1761 | |
| 1,000 | 0.0294 | 0.0928 | 0.1844 | ||
| LabelPowerset | 800 | 0.0062 | 0.0610 | 0.3115 | |
| 1,000 | 0.0066 | 0.0620 | 0.3113 | ||
| USPTO | MLkNN | 12,000 | 0.1142 | 0.2692 | 0.0643 |
| 18,000 | 0.1152 | 0.2673 | 0.0618 | ||
| RAkEL | 12,000 | 0.0421 | 0.1038 | 0.0588 | |
| 18,000 | 0.0423 | 0.1102 | 0.0587 | ||
| LabelPowerset | 12,000 | 0.0273 | 0.1161 | 0.0594 | |
| 18,000 | 0.0274 | 0.1151 | 0.0624 |
5.2.3 TextCNN, TextRNN, RCNN
The Neural Classifier toolbox (Liu et al., 2019) implements the TextCNN, TextRNN and TextRCNN models. This toolbox takes into consideration the hierarchical structure of the labels in the format of tree or Directed Acyclic Graph (DAG). Since the labels in our datasets have a clear hierarchical structure (cf. Table 2 ), the switch corresponding to this structure is turned on. Apart from the training and test sets, a validation set is prerequisite for this toolbox. In this study, we choose randomly one-tenth of the test set as the validation set. Another important parameter is the top number of labels which are most likely to be assigned to an instance (top_k). This work fixes this parameter to the maximum number of labels per instance in each dataset (cf. the second column in Table 7 ).
Table 7. Performance of the TextCNN, TextRNN and TextRCNN with different parameter settings on three real-world datasets. |
| Datasets | Top_k | Model | Macro F1 | Micro F1 | Hamming loss |
|---|---|---|---|---|---|
| Health-Sciences | 7 | TextCNN | 0.0883 | 0.2489 | 0.2304 |
| TextRNN | 0.0788 | 0.2341 | 0.1256 | ||
| TextRCNN | 0.0836 | 0.2294 | 0.1359 | ||
| Biological-Sciences | 4 | TextCNN | 0.3070 | 0.4693 | 0.5055 |
| TextRNN | 0.2026 | 0.4202 | 0.2548 | ||
| TextRCNN | 0.3114 | 0.5094 | 0.4714 | ||
| USPTO | 65 | TextCNN | 0.0341 | 0.2018 | 0.0127 |
| TextRNN | 0.0301 | 0.2437 | 0.0107 | ||
| TextRCNN | 0.0401 | 0.2408 | 0.0089 |
In addition, due to high computing power needed to train these three models, Google’s free server Colab (GPU 12G) is used for the Biological-Sciences and Health-Sciences datasets, and Ali Cloud server (GPU 32G) for the USPTO dataset.
From Table 7 , it is not difficult to see that the TextCNN and TextRCNN models outperform the TextRNN model in terms of macro F1 and micro F1, but the TextRNN model performs best in terms of Hamming loss. Another interesting observation is that these models tend to perform worse on the datasets with more unbalanced label-document distribution and more complex label hierarchies. The challenge for multi-label classification task is still the huge label space as well as the hierarchy and depth of label structure.
5.3 General remarks
For the convenience of readers, the experimental results of the above seven methods are summarized in Table 8 Table 8 just depicts the best performance in terms of three evaluation measures, but the resulting parameters may not be consistent. From Table 8 , the following conclusions can be drawn:
Table 8. Performance of seven multi-label classification methods on three real-world datasets. |
| Dataset | Method | Macro F1 | Micro F1 | Hamming Loss |
|---|---|---|---|---|
| Biological-Sciences | Dependency LDA | 0.0443 | 0.0102 | 0.2537 |
| MLkNN | 0.0836 | 0.1535 | 0.3389 | |
| RAkEL | 0.0280 | 0.0794 | 0.2859 | |
| LabelPowerset | 0.0044 | 0.0219 | 0.3845 | |
| TextCNN | 0.3070 | 0.4693 | 0.5055 | |
| TextRNN | 0.2026 | 0.4202 | 0.2548 | |
| TextRCNN | 0.3114 | 0.5094 | 0.4714 | |
| Health-Sciences | dependency LDA | 0.0412 | 0.0102 | 0.2542 |
| MLkNN | 0.0806 | 0.1364 | 0.2727 | |
| RAkEL | 0.0294 | 0.0928 | 0.1761 | |
| LabelPowerset | 0.0066 | 0.0620 | 0.3113 | |
| TextCNN | 0.0883 | 0.2489 | 0.2304 | |
| TextRNN | 0.0788 | 0.2341 | 0.1256 | |
| TextRCNN | 0.0836 | 0.2294 | 0.1359 | |
| USPTO | dependency LDA | 0.0026 | 0.0012 | 0.0895 |
| MLkNN | 0.1152 | 0.2692 | 0.0618 | |
| RAkEL | 0.0423 | 0.1102 | 0.0587 | |
| LabelPowerset | 0.0274 | 0.1161 | 0.0594 | |
| TextCNN | 0.0341 | 0.2018 | 0.0127 | |
| TextRNN | 0.0301 | 0.2437 | 0.0107 | |
| TextRCNN | 0.0401 | 0.2408 | 0.0089 |
(1) For the datasets with small data size and balanced document-label distribution, the TextCNN and TextRCNN models should be preferred. In more detail, both the Biological-Sciences and the Health-Sciences datasets have smaller number of documents and labels, more balanced document-label distribution than the USPTO dataset. The TextCNN model shows obvious superiority on these two datasets, especially the Biological-Sciences dataset.
(2) For extremely large datasets with unbalanced document-label distribution, the MLkNN algorithm is more effective. For the USPTO dataset, the maximum number of labels assigned to an instance is 65. This means that we need to make a judgment on the top 65 labels for each instance. The top number of labels of the other datasets is 4 and 7 respectively, which is much simpler than the USPTO dataset. The MLkNN algorithm can effectively avoid this kind of individual judgment. To say it in another way, this algorithm is more suitable for large datasets with skewed document-label distribution by simply calculating the distance between the k instances of known categories closest to the instance, and then assigning labels according to the principle of minimum distance.
Additionally, we have calculated the Spearman’s rank correlation coefficients among the Macro F1, Micro F1, and Hamming loss metrics, as presented in Table 8 . The analysis reveals a robust positive correlation between Macro F1 and Micro F1 (0.76), indicating a strong relationship. However, no significant correlation is detected between Macro/Micro F1 and Hamming loss. This indicates that different dimensions of multi-label classification tasks are measured by macro/micro F1 and Hamming loss. In the context of multi-label classification research and applications, it is imperative to choose evaluation metrics with flexibility, taking into consideration their respective strengths and weaknesses, as well as the specific context in which they are applied.
Table 9. Spearman correlation coefficients among Macro F1, Micro F1, and Hamming Loss. |
| Macro F1 | Micro F1 | Hamming loss | |
|---|---|---|---|
| Macro F1 | 1.000 | 0.762 | 0.277 |
| Micro F1 | 0.762 | 1.000 | -0.008 |
| Hamming loss | 0.277 | -0.008 | 1.000 |
6 Conclusion
The multi-label classification is a very popular problem in the field of scientometrics, informetrics, and many others. Many multi-label classification methods with good performance on the benchmark datasets have been proposed in the literature. However, many real-world multi-label datasets show different characteristics from benchmark ones. Therefore, this study devotes to exploiting comprehensively the applicability and power of seven representative approaches in three open-source toolkits. More specifically, after three real-world datasets (Biological-Sciences, Health-Sciences, and USPTO) are constructed, the resulting parameters in each approach are tuned. Then, extensive experiments are conducted and the following insights can be obtained.
(1) The Biological-Sciences and the Health-Sciences datasets have complex hierarchical labels, and the number of documents and labels is relatively small, and the document-label distribution is more balanced than the USPTO dataset. Two deep learning-based models, TextCNN and TextRCNN, show obvious superiority on these two datasets.
(2) The MLkNN algorithm only needs to measure the distance between the nearest k instances of known categories and an interested instance, and then allocate labels according to the principle of minimum distance. This property enables the MLkNN algorithm to be more suitable for a large dataset with skewed document-label distribution.
(3) The neural classifier toolbox can benefit greatly from the GPU and the advanced deep learning technique (Chen et al., 2020). The Scikit-Multilearn library encapsulates a lot of conventional machine learning methods for the multi-label classification task. It is very convenient for users to use, but not all the methods have good performance. Compared to neural classifier toolbox and Scikit-Multilearn library, the dependency-LDA doesn’t have obvious advantages in terms of three evaluation measures. But one can observe a better distinction between rare and common labels than the counterparts.
(4) In general, no matter which method is adopted, it is difficult to obtain satisfactory performance on the real-world datasets. Though, it seems that the approaches based on deep learning techniques seem to be more promising, since they can consider the hierarchical structure and inter-dependency between the labels. In the near future, the performance of multi-label classification tasks should be still improved greatly to reach a practical level.
Funding information
This work was supported partially by the Natural Science Foundation of China (Grant Numbers 72074014 and 72004012).
Data availability
Three real-world datasets (Biological-Sciences, Health-Sciences, and USPTO) from SciGraph and USPTO database are constructed. The datasets utilized in this study are publicly accessible and can be retrieved from their official websites as follows: SciGraph can be accessed at https://www.springer.com/gp/about-springer/media/press-releases/corporate/springer-nature-scigraph--supporting-open-science-and-the-wider-understanding-of-research/12129600, and the United States Patent and Trademark Office (USPTO) dataset is available at https://bulkdata.uspto.gov/data/patent/grant/redbook/bibliographic/2019/.
Author contributions
Shuo Xu(xushuo@bjut.edu.cn) developed the study concept and design. Yuefu Zhang(yaogeng_z@163.com) and Sainan Pi(silencepipi@outlook.com) analyzed and interpreted the data. Xin An(anxin@bjfu.edu.cn) monitored the process of this study. Yuefu Zhang drafted the manuscript, and all authors provided critical revisions for important intellectual content. The study was supervised by Shuo Xu. All authors read and approved the final manuscript.