1 Introduction
In today’s world of scientific exploration and technological progress, the significance of collaboration has grown alongside the rising complexity of scientific challenges (Laudel, 2001; Sonnenwald, 2007). This increased complexity requires collective efforts, making collaboration more essential than ever. Collaborative initiatives enhance research by bringing in a variety of perspectives from different disciplines, which are crucial for effectively tackling complex challenges. This idea is backed by influential studies that illustrate how collaborations draw upon diverse expertise and viewpoints, improving the capacity to understand and solve intricate scientific problems (Huang et al., 2023; Klein, 2005; Qin et al., 1997).
The mechanisms of scientific collaboration often manifest through co-authorships in articles and patents (Barber & Scherngell, 2013; Huang et al., 2024; Newman, 2001; 2004). In separate studies across various fields, including biomedical research, physics, and mathematics, Newman identified that most scientists have a limited number of collaborators, while a few have hundreds or even thousands (Newman, 2004). Understanding collaboration patterns is crucial to comprehending the evolution of scientific progress. Guimerà et al. (2005) studied factors like team size and involvement of newcomers and found that team composition significantly influences both collaboration structures and outcomes in both the arts and sciences. Similarly, Tomassini and Luthi observed the dynamics of collaborative networks in genetic programming, recognizing the changing nature of these ties (Tomassini & Luthi, 2007). It is, therefore, essential to understand the collaboration practices of scientists to better learn how networks develop and function, which in turn, can inform strategies to improve collaboration in scientific research and innovation.
Building on this understanding of collaborative patterns, the researches by Barabâsi et al. (2002) and Barber and Scherngell (2013) further reinforce the significance of co-authorship networks within the scientific community. These studies reveal that such networks are not uniformly structured but are composed of distinct substructures, underscoring their scale-free nature. This characteristic is shaped by both internal and external co-authorship links, influencing the networks’ scaling and topological evolution (Fortunato, 2010). Additionally, the identification of communities within these networks, as indicated by Van Nguyen et al. (2012), is heavily reliant on the density of links within groups compared to those between them.
The effective detection of communities within these networks is a pivotal aspect of network analysis, as highlighted by Reichardt and Bornholdt (2006), Fortunato and Hric (2016). This process, which unravels the few clusters in intricate networks, offers invaluable insights into the organizational and functional structures therein. The journey of methodologies for community detection spans from foundational graph-theoretical approaches to the use of advanced machine learning and has been a key factor in identifying communities within various networks (Ng et al., 2001; Zhang et al., 2009; Zhao et al., 2005). The field has been greatly advanced by the application of deep learning, probabilistic modeling, and multi-resolution strategies for the purposes of discovering communities within expansive and varied networks (Liu et al., 2020; Rosvall et al., 2009; Zhang et al., 2009). Zhang et al.(2023) applied the attributed network clustering algorithm (Falih et al., 2018) to understand the collaborations among statisticians better, and Mao et al. (2017) leveraged machine learning and network theory to detect topical scientific communities. Such innovative approaches not only support the analysis of collaboration patterns but also encourage strategic research and offer a window into the collaborative evolution of scientific knowledge.
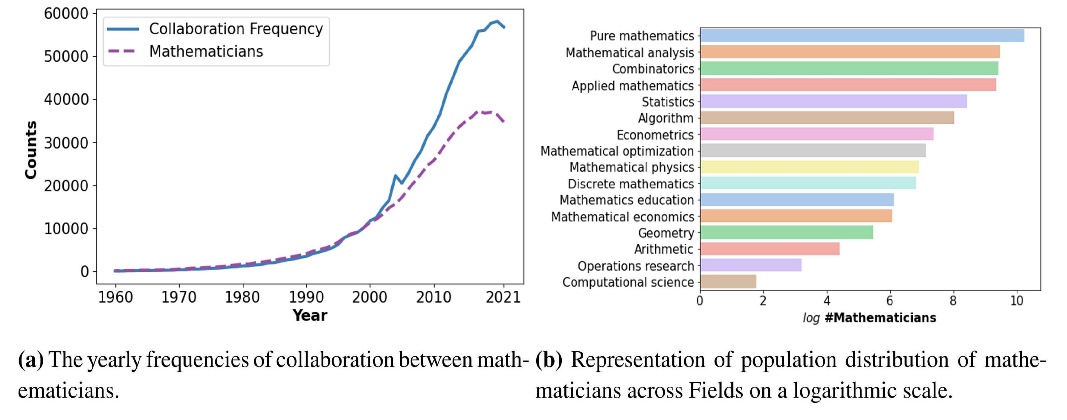
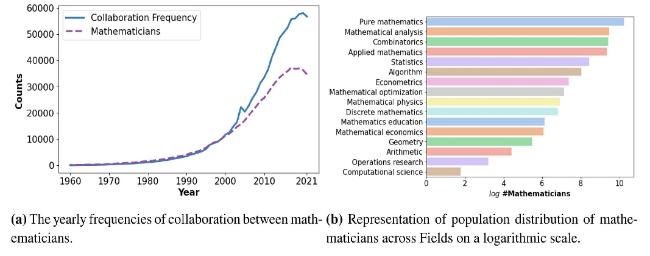
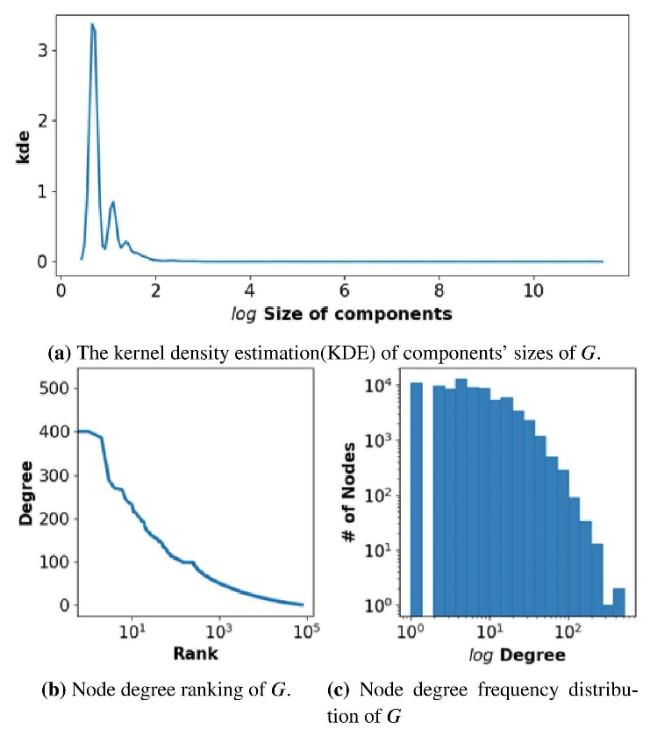
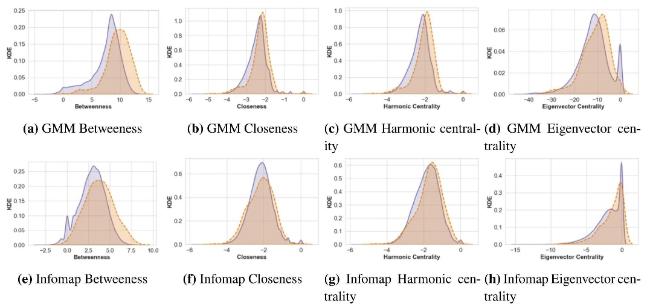
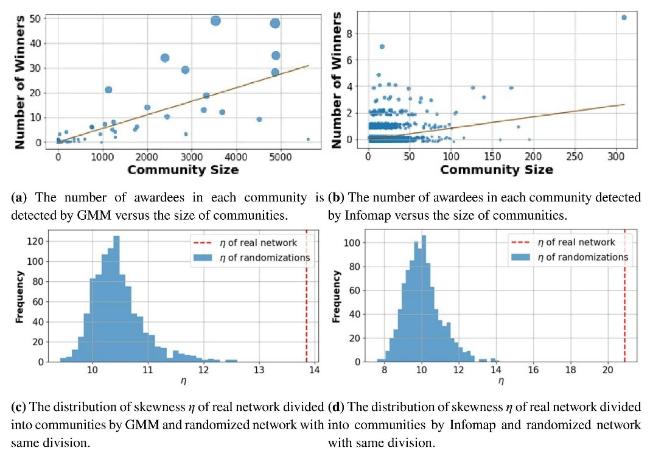
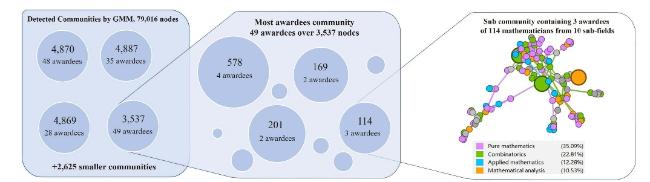
Recognizing the unique role of mathematics as a foundational language across scientific areas and its importance in fostering research collaborations, our study specifically investigates the collaboration network of mathematicians (Asif & Islam, 2016; Grossman, 2002). With this in mind, we focus on scientific collaboration and career development within the mathematical circle and wonder what the underlying community structure in the collaboration network of mathematicians is and what roles elite ones play within their communities compared with their peers. These research questions aim to identify and analyze communities within the collaboration network, shedding light on the collaborative characteristics of elite mathematicians and their peers in advancing mathematical research. To achieve this, the study draws publication data from OpenAlex (Priem et al., 2022), an open dataset, and collects supplementary information on mathematical awards. Focusing on collaborations among mathematicians, including recipients of prestigious awards in the field of mathematics such as the Fields Medal and Lobachevsky Prize, the research aims to uncover and delineate clusters of collaborations within this network by applying two community detection algorithms: Greedy Modularity Maximization (GMM) (Clauset et al., 2004) and Infomap (Rosvall et al., 2009). Subsequently, a detailed analysis of these detected communities will be conducted, probing into their inherent characteristics, such as collaborative traits and impact within distinct mathematical sub-fields.
Investigating the network characteristics of mathematicians, particularly those who are award laureates, is a vital part of modern scientific research. This study aims to understand how these mathematicians are positioned within collaboration networks and the impact they have on these communities. By examining the roles, influence, and structural formations of these mathematicians, especially those who have received prestigious awards, we aim to shed light on the dynamics of their collaborative interactions. The insights gained from this research will enhance our understanding of collaborative networks in mathematics and provide valuable perspectives on the dynamics and evolution of scientific collaboration across various disciplines.
Table 1. The basic characteristics of mathematicians’ collaborative networks. |
| N | L | 〈k〉 | lnN | 〈C〉 | density |
|---|---|---|---|---|---|
| 79,016 | 342,022 | 8.657 | 11.2774 | 0.1972 | 0.0001 |
2 Methodology
2.1 Collaboration network
In this study, we leverage the extensive dataset from OpenAlex, a key resource for our analysis. Our study collected data on scholars who fulfilled specific requirements: they were prolific authors with more than ten publications between 1960 and 2021. We classified authors primarily active in mathematics and identified collaborative links among them. Figure 1(a) shows a significant rise in collaboration among mathematicians after 2005, reflecting the necessity to tackle complex problems requiring interdisciplinary cooperation. Additionally, we compiled information on renowned mathematicians who have received awards in their field from platforms including Wikipedia, Wikidata, and official award websites. This supplementary dataset encompasses 341 unique award categories and includes detailed information on the mathematicians’ demographics and achievements. Of these distinguished award recipients, 395 individuals were successfully matched with profiles in the OpenAlex database.
Figure 1. Data characteristics of mathematicians. |
This data collection methodology enabled us to gain insights into the collaborative networks of 79,016 mathematicians affiliated with 8,833 institutions across 172 countries. We were also able to categorize their main areas of research within mathematics, including fields like pure mathematics, mathematical analysis, combinatorics, and statistics, as shown in Figure 1(b) . Following this, we constructed an undirected weighted collaborative network, designated as G, where mathematicians are represented as nodes v1, v2, ⋯, vN. The edges $l_{v_{i}v_{j}}$ and their respective weights $w_{v_{i}v_{j}}$ represent the collaborative connections and the frequency of collaborations, respectively, over the period from 1960 to 2021 (Priem et al., 2022).
In our network G, the average degree 〈k〉 is lower than the logarithm of the number of nodes lnN, indicating that the network’s interconnections are relatively sparse. This is further supported by the network density being less than 0.002, suggesting sparser connectivity than one might expect in a denser network. This finding implies that the collaboration network among mathematicians is characterized by less dense interconnections, with fewer links connecting the nodes than in a more interconnected network. We then examined the structural attributes of network G using various analytical methods, with the results visualized in Figure 2. Initially, we applied kernel density estimation (KDE) to assess the distribution of connected component sizes within G. The visualization of this analysis distinctly illustrates a significant polarization in component sizes, indicating stark differences in the community structures present. Next, we analyzed node degree ranking to understand the relative importance or centrality of nodes in G. Figure 2(b) highlights critical nodes or ‘hubs’ in the network, suggesting the presence of highly connected individuals. Furthermore, we generated a histogram to depict the frequency distribution of node degrees in G, providing insights into the range and scarcity of specific node degrees and enhancing our understanding of the network’s connectivity patterns. These comprehensive analyses collectively shed light on the structural properties of the collaboration network G, offering valuable insights into its network dynamics.
Figure 2. Network characteristics. |
2.2 Metrics of centrality
In network analysis and statistical modeling, centrality metrics are crucial for evaluating the significance or influence of nodes within a network. These metrics are instrumental in deciphering the network’s structural nuances and the dynamics of influence and information flow. This paper highlights four primary centrality measures, each offering unique insights into nodes’ roles within weighted networks: Betweenness, Closeness, Harmonic centrality, and Eigenvector centrality. For this analysis, we employed the Python interface of igraph (Csardi & Nepusz, 2006) to execute and calculate four key centrality metrics. Here, dw (u, v) denotes the weight-adjusted shortest path between nodes u and v.
Betweenness. Betweenness is delineated by the degree to which a node falls on the shortest paths interlinking other nodes. Nodes with high Betweenness are akin to connectors or intermediaries and play a crucial role in the network’s efficient communication. Mathematically, it is defined as the total number of shortest paths that traverse through a particular node and is given by:
$\operatorname{Betweenness}(v)=\sum_{s \neq v \neq t} \sigma_{s t}^{w}(v),$
where $\sigma_{s t}^{w}(v)$ is the tally of these shortest weighted paths from node s to node t via node v.
Closeness. Closeness evaluates a node’s proximity to all other nodes, advocating for the importance of nodes that can rapidly connect with the rest. Higher closeness indicates a node’s strategic position for swift information spread across the network. The closeness for a node is computed as the inverse sum of its shortest path distances to all other nodes:
$\operatorname{Closeness}(v)=\frac{1}{\sum_{u \neq v} d^{w}(u, v)},$
Harmonic centrality. Harmonic centrality modifies the concept of closeness centrality by focusing on the reciprocal of the weighted shortest paths from one node to all others rather than averaging these distances. This subtle difference shifts the emphasis toward the influence exerted by shorter paths within the network. Harmonic centrality is summed up as follows:
$C_{H}(v)=\sum_{u \neq v} \frac{1}{d^{w}(u, v)},$
This measure emphasizes nodes that are not only close to other nodes but also connected to a wide range of other nodes, contributing to global network accessibility and cohesion.
Eigenvector centrality. Eigenvector centrality reflects a node’s prestige by recognizing that connections to influential nodes amplify a node’s score. In essence, nodes with extensive connections to other central nodes are deemed pivotal. The centrality score is iteratively derived from the neighbor’s scores, defined by the following relation:
Ax=λx
where A is the adjacency matrix reflecting the network’s connections with edge weights, x corresponds to the principal eigenvector given by the highest eigenvalue λ of A and the individual centrality score CE(v) for node v is denoted by its respective value in x.
3 Findings
3.1 The influence of elite mathematicians in communities
The study of elite mathematicians within academic communities is instrumental in unraveling the complexities of knowledge sharing, collaborative patterns, and the structure of scholarly networks. This exploration, particularly through the lens of network analysis, has become a vital aspect of modern research (Asif & Islam, 2016; Gaskó et al., 2016; Izquierdo et al., 2018). Our research identifies these elite mathematicians based on their significant career achievements, namely their receipt of notable awards in mathematics. We then segment collaboration networks into distinct communities using two algorithms and focus on calculating the four aforementioned centrality metrics within these communities. This method provides a deeper insight into the dynamics of centrality and the critical role these eminent figures play in the formation and evolution of academic networks.
The outcomes, outlined in Table 2 and depicted in Figure 3 , reveal a distinct trend when comparing award-winning mathematicians with their peers. Significant differences in Betweenness, Closeness, and Harmonic Centrality between these two groups were identified, showing statistically meaningful variations (p < 0.05) through a t-test when computing centralities focused on the sub-network formed by the community division via the community detection algorithm. The heightened Betweenness Centrality among award recipients suggests their pivotal role as vital links or intermediaries among diverse nodes within the communities. Their elevated status implies a substantial influence over the shortest paths connecting other nodes. Conversely, the lower Betweenness Centrality among other mathematicians indicates a potential lack of intermediary roles, signaling a different function or position within the network’s structure. Moreover, awardees exhibit superior Closeness and Harmonic Centrality metrics. The increased Closeness implies that awardees are more swiftly connected to other nodes, maintaining shorter average distances compared to non-recipients. This suggests enhanced and more direct communication channels within the group of awardees. Additionally, the heightened Harmonic Centrality among awardees highlights not only their proximity to others but also shorter harmonic mean distances, indicating more effective communication routes and a stronger sense of interconnectedness within their subgroup.
Table 2. The t-test of the difference of centrality metrics between awardees and other mathematicians. |
| Betweenness | Closeness | Harmonic centrality | Eigenvector centrality | |
|---|---|---|---|---|
| GMM | 47,777.2381*** | 0.0141*** | 0.0245*** | -0.0455*** |
| Infomap | 96.5236*** | 0.0053 | 0.0323*** | 0.1148*** |
***p<0.001, **p<0.01, *p<0.05 |
Figure 3. Four centrality metrics were computed within communities identified by both GMM and Infomap, and subsequently compared between awardees and other mathematicians. The metrics assessed were: (a), (e) Betweenness; (b), (f) Closeness; (c), (g) Harmonic Centrality; and (d), (h) Eigenvector Centrality. |
The analysis of eigenvector centrality for awardees shows contrasting results between communities identified by GMM (negative) and Infomap (positive). As previously discussed, although both algorithms uncover community structures, they operate on different principles and exhibit distinct strengths. GMM is straightforward but may encounter resolution limits, hindering its ability to detect very small or loosely connected communities. In contrast, Infomap is adept at identifying community structures in large, modular networks, typically resulting in more balanced community sizes. This is the consequence that in larger networks, eigenvector centrality tends to exhibit greater consistency. The complexity and sheer number of nodes in these extensive systems reduce the influence of minor connectivity changes on individual nodes’ eigenvector centrality, thereby enhancing their stability. Conversely, in smaller networks, certain nodes might display heightened eigenvector centrality due to simpler connection patterns, potentially leading to concentrated control of information flow among a few nodes. An examination of eigenvector centrality across the entire collaboration network reveals no substantial difference between awardees and their peers (−0.00127 with p-value of 0.4771). This implies that both award-winning and non-award-winning mathematicians exert a similar level of influence throughout the network, pointing to a comparable effect on the network’s structural dynamics and their capacity to direct the flow of information.
3.2 Imbalanced distribution of talent mathematicians within communities
Researchers frequently collaborate with familiar individuals, such as mentors, past research colleagues, or established experts in their academic domain (Singh et al., 2021; Yu et al., 2021). These collaborations form complex networks characterized by well-established connections, notably evident in scholarly co-authorship. Understanding these connections is crucial in exploring scientists’ intricate collaboration patterns and identifying cohesive clusters or communities within academic networks.
In our study of mathematicians’ collaboration network, we employed two community detection algorithms, namely GMM and Infomap. The first one identified 2,629 communities within network G, while the last one delineated 8,962 communities. Among these structures, the positioning of 395 award-winning mathematicians did not display an even distribution. As depicted in Figure 4(a) where each circle represents a community, and the radius is positively proportional to the number of awardees in this community. The community sizes identified by GMM showed a partially positive correlation with the presence of awardees. Notably, the community hosting the most awardees did not align with its overall size. Conversely, Infomap exhibited a modest positive link between community size and the number of awardees, notably observed in the largest community harboring the most awardees. This finding prompts consideration of an “elite mathematician” accumulation effect, suggesting that awardees tend to collaborate within their elite circle or with potential awardees in the field of mathematics. This encourages a further exploration of how award recipients are distributed across various communities by involving the statistical measure of skewness (Groeneveld & Meeden, 1984), formally defined by the following equation:
$\eta=\frac{1}{n} \frac{\sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)^{3}}{\left(\frac{1}{n} \sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)^{2}\right)^{3 / 2}}$
where we denote the sizes of detected communities as c1, c2, ⋯, cn, and the tally of awardees within these communities as a1, a2, ⋯, an. Here, $x_{i}=\frac{a_{i}}{c_{i}}-\frac{\sum_{i=1}^{n} a_{i}}{\sum_{i=1}^{n} c_{i}}$ signifies the deviation between the actual proportion of awardees in the i-tℎ community and the average awardee ratio across the entire network of collaborations. The skewness η quantifies the asymmetry of the data distribution around its mean. In essence, for the array of discrepancies x1, x2, ⋯, xn reflecting the variation between the observed and expected ratios of awardees in each community skewness measures how asymmetric these deviations are from their mean.
Figure 4. Distributed characteristics of mathematicians and mathematical awardees within communities. |
In examining whether awardees are evenly distributed across communities, we postulate a straightforward, linear correlation between the number of awardees and the size of each community. To test this idea, we implemented a statistical simulation for randomly allocating awards among different communities. This simulation allocated awardee numbers across communities using a multinomial distribution F~Multinomial(nawardee, p1, p2, …, pn), where nawardee = 395 represents the total number of awardees. The probabilities $p_{1}=\frac{c_{1}}{N}, p_{2}=\frac{c_{2}}{N}, \cdots, p_{n}=\frac{c_{n}}{N}$ correspond to each
community’s size as a fraction of the total size of the collaboration network G. This method helps us understand the potential random distribution of awardees across the network’s communities.
Next, we ran 1,000 random simulations using the described multinomial distribution F to evaluate the connection between community size and awardee distribution. These simulations allowed us to compute skewness values for the synthetically distributed awardees according to the community structures detected by GMM and Infomap, notated as ηj1 and ηj2 for each j of the 1,000 simulations, respectively. For comparative purposes, we determined the actual skewness values, η1 and η2, drawn from the real network’s community structures as segmented by GMM and Infomap. Our goal in comparing the simulated and real data distributions was to assess the homogeneity between what is expected and what is observed. As shown in Figure 4 (c) and (d) , both η1 and η2 values notably surpass the range of random 𝜂 distributions. The skewness of awardees distribution in real network communities is more pronounced than in the randomized models. This indicates a tendency for award-winning mathematicians in actual networks to cluster more densely in certain communities rather than being evenly spread across the network, resonating with the principles of club theory in economics (Potts et al., 2017).
3.3 Community and research direction
Furthermore, we explore the complex interplay between the research orientations of mathematicians and the communities identified within their collaboration network, categorizing them into 16 distinct mathematics sub-fields (see Figure 1(b) ). To evaluate the congruence between these sub-fields and the communities delineated by two different algorithms, we apply the NMI (Details mentioned in the Appendix). For the purpose of robustness verification, this section designs a random experiment where discipline labels are randomly assigned to all nodes in the network, and the NMI values between community labels and random discipline labels are calculated for different algorithms. Through 1,000 repeated experiments, the study obtains the range of NMI values between community labels and discipline labels under random experiments. Comparing the communities identified by both algorithms against a random reassignment of sub-field labels for each mathematician, Table 3 reveals a significant positive correlation between the communities and the sub-fields. This implies that the identified communities inherently reflect aspects of these sub-fields, suggesting a natural tendency for mathematicians working in similar areas to collaborate more frequently.
Table 3. NMI analysis between true field labels and detected community labels. |
| Method | GMM | Infomap |
|---|---|---|
| Real NMI | 0.2222 | 0.2404 |
| Random NMI | (0.03361, 0.03365) | (0.08247, 0.08250) |
These insights lead us to question whether the community information, encapsulating aspects of mathematical sub-fields, could be effectively represented using different methodologies. In particular, we explore the relationship between the number of award recipients in a community, the community’s disciplinary makeup, and its size. To analyze the structured nature of field labels within these communities, we introduce the Simpson index (Simpson, 1949; Somerfield et al., 2008). Our linear regression analysis, examining the relationship between the number of awardees, community sizes, and the Simpson index (indicative of disciplinary composition), yields compelling findings. The results displayed in Table 4 indicate that larger communities tend to have more award recipients, consistent with earlier observations in this study. Conversely, there is an inverse correlation between the Simpson index and the number of awardees. This suggests that communities with higher diversity in their field labels or greater disorderliness are less likely to include award recipients. This finding implies that mathematicians who specialize in specific subdomains and collaborate intensively within those domains are more likely to achieve notable success in their field.
Table 4. Linear regression analysis on the number of awardees. |
| #awardees | ||
|---|---|---|
| Algorithm | GMM | Infomap |
| Community size | 0.0056*** | 0.0092*** |
| Simpson index | -0.1075* | -0.0339*** |
***p<0.001, **p<0.01, *p<0.05 |
4 Discussion
In our study, which centers on mathematicians and their collaborative networks, we strive to uncover the underlying community structures and collaboration patterns prevalent among scholars in the field of mathematics. A key aspect of our investigation is the distinct role played by award-winning mathematicians within these networks. Employing two robust community detection algorithms GMM and Infomap our research delineates the collaboration clusters that involve these distinguished mathematicians. Our study, thereby, illuminates not just the collaborative behaviors of elite mathematicians but also the broader structure of knowledge dissemination and its impact on the evolution of the field. By analyzing the roles and patterns of award-winning mathematicians, we gain a deeper understanding of the forces shaping mathematical research and its progression.
This study delves into the roles and impacts of elite mathematicians within academic networks, with a particular focus on their influence, which is evaluated using centrality metrics. The results show that mathematicians who are award recipients exhibit higher Betweenness, Closeness, and Harmonic centrality than their peers who haven’t received such awards. This suggests they have a more influential or connective role within networks.
Additionally, awardees are found to concentrate their collaborations within certain communities as opposed to engaging equally across the entire collaboration network. Randomized trials support these findings, indicating a tendency for awardees to cluster within particular communities. They are not only central in terms of their connections but also in their ability to bridge different clusters within the network, facilitating the flow of ideas and collaborations across disciplinary boundaries specific to mathematicians.
Furthermore, our examination of the connections between mathematical sub-fields and the communities detected by the two algorithms shows a significant positive correlation. This suggests that collaboration within the mathematician community loosely reflects these sub-fields, with individuals in similar areas tending to work together. This underscores the role of community structures in shaping research trajectories and the evolution of mathematical knowledge, highlighting how mathematicians in similar sub-fields collaborate to enhance coherence and specialization within their respective communities.
Lastly, the study examines the relationship between the number of awardees, the disciplinary diversity within communities, and the sizes of these communities. The analysis indicates that mathematicians are more likely to achieve success in their field when they specialize in specific subdomains and participate extensively in collaborations within those subdomains. Moreover, our findings highlight the need for interdisciplinary approaches in studying interdisciplinary scientific collaboration. By extending our analysis beyond mathematics to include interactions across various scientific disciplines, future research can provide a more comprehensive understanding of collaborative dynamics and community structures in science. This broader perspective is crucial for addressing complex global challenges that require interdisciplinary solutions.
The primary limitation of this study is its focused examination of mathematicians and their awardees. This specific concentration may restrict the applicability of our findings to the broader scientific community. By directing our attention to a select group of scholars, we may not fully capture the collaborative patterns and community structures that exist across a wider range of scientific disciplines.
Consequently, future research would benefit from adopting an interdisciplinary approach. Given the increasing focus on inter- disciplinary collaboration in contemporary research, it is imperative to investigate how collaborations span different scientific domains. This would entail broadening our scope beyond mathematics to encompass interactions between mathematicians and researchers from various other fields. Additionally, this study encounters a data limitation due to the potential incompleteness of the dataset on mathematics awardees, a consequence of the manual online data collection process. This method could introduce issues such as data omissions and challenges in achieving a comprehensive dataset. The reliance on manually collected online data may result in inaccuracies due to inconsistencies in award reporting, the frequency of information updates, and variability in data accessibility. Although we have considered edge weights in GMM and Infomap, the application of other community detection methods like the k-clique method are also important in future work to obtain more robust results and conduct horizontal comparisons. Incorporating the k-clique method could provide additional insights into the tightly-knit sub-communities within the collaboration network, further enhancing the robustness and depth of our analysis.
These limitations could compromise the depth and reliability of our findings, particularly those concerning the roles and impacts of awardees in the mathematical community’s collaborative networks. Future studies would greatly benefit from more systematic and automated data collection methods, which would likely reduce the occurrence of incomplete data and lead to more thorough and precise analyses. Moreover, the development of new community detection algorithms specifically designed for the distinctive characteristics of scientific networks could substantially improve the precision of community identification. This tailored approach would enable a more accurate understanding of the collaborative dynamics across various scientific fields.
Appendix
1 Data collection
In this study, we leverage the extensive dataset from OpenAlex, a key resource for our analysis. OpenAlex provides a broad and openly accessible collection of scholarly works, encompassing authors, publication venues, institutions, and key concepts. This dataset, which is regularly updated, includes more than 243 million publication records and 90 million author profiles, along with detailed information on publishers, funders, and institutions. Unique IDs assigned to each scientific entity in OpenAlex help alleviate issues of name disambiguation. Research utilizing this dataset has been instrumental in understanding career patterns and the evolving dynamics within scholarly networks. OpenAlex has been widely used in the science of science research, enabling studies on collaboration patterns, individual career trajectories, and the overall framework of scholarly interactions (Harris et al., 2023; Williams et al., 2023; Xu et al., 2024).
Using OpenAlex, our study collected data on scholars who fulfilled specific requirements: they were prolific authors with more than ten publications between 1960 and 2021. We initially screened the literature from this period, scrutinizing authorship ties and their respective primary disciplines, as defined by level 0 in OpenAlex’s classification system. This process allowed us to pinpoint those authors whose main scholarly output was in the field of mathematics. Having classified these individuals as mathematicians, we further identified collaborative links among them, focusing on publications where their co-authors were also recognized as mathematicians.
Upon examining the graph presented in Figure 1 (a), which illustrates the collaborative frequency among mathematicians across time and the annual count of active mathematicians, a notable trend is observed. There has been a significant rise in collaboration among mathematicians, particularly after 2005. Although there has been growth in the number of mathematicians during this period, this increase has not been proportional to the rapid escalation in collaborative activities. The intensified collaborative efforts reflect the necessity to tackle complex problems in today’s technologically advanced landscape, where interdisciplinary cooperation and larger research teams are often required. These patterns have resulted in substantial collaborative network data, underscoring the importance of these joint academic pursuits.
In addition to using OpenAlex for publication records, we have carefully compiled information on renowned mathematicians who have received awards in their field. This supplementary dataset was sourced from a combination of platforms, including Wikipedia, Wikidata, and official award-related websites. It includes detailed information such as the mathematicians’ names, genders, birth years, specific award titles, and the dates these awards were received. Importantly, this dataset encompasses 341 unique award categories. Among the top ten are the John Simon Guggenheim Memorial Foundation Fellowship, Fellow of the Royal Society, Order of the Red Banner of Labor, Fields Medal, Lenin Prize, National Medal of Science, Order of Lenin, Leroy P. Steele Prize, Lobachevsky Prize, and State Stalin Prize. The mathematicians in this dataset, born between 1,741 and 2,000, show a gender distribution of 521 males and 27 females. Of these distinguished award recipients, 395 individuals were successfully matched with profiles in the OpenAlex database.
2 Community detection
In this study, we introduced two widely-used community detection algorithms: GMM and Infomap to explore the sub-community structure in the collaboration network of mathematicians. Both GMM and Infomap are applied to weighted undirected networks, with their implementations in the igraph Python interface taking edge weights into consideration (Csardi & Nepusz, 2006). GMM is based on the maximization of modularity using a greedy algorithm, while Infomap is grounded in the principles of information theory. These two classic methods were chosen due to their robust theoretical foundations and their ability to effectively analyze the community structure within the collaboration network.
2.1 Greedy Modularity Maximization
Let AN×N be the adjacency matrix of the collaboration network G, the element Auv of A satisfies
$A_{u v}=\left\{\begin{array}{cc} w_{u v}, & \text { if mathematicians } u \text { and } v \text { had co-authored, } \\ 0, & \text { otherwises } \end{array}\right.$
In the context of communities, mathematicians may form clusters based on different community detection algorithms. The key measure for assessing the performance of such an algorithm is modularity, which can be mathematically described as follows:
$Q=\frac{1}{2 m} \sum_{u v}\left[\boldsymbol{A}_{u v}-\frac{k_{u} k_{v}}{2 m}\right] \delta\left(c_{u}, c_{v}\right).$
Here, $m=\frac{1}{2} \sum_{u v} \mathbf{A}_{u v}$ represents the total number of edges within the graph G, where cu denotes the community belonging to mathematician u. The term ku=∑vAuv refers to the degree of mathematician u, the count of edges connected to it. The function δ(x,y) is an indicator function with a value of 1 when x = y and 0 otherwise.
The proportion of edge endpoints connected to community i is indicated as: $a_{i}=\frac{1}{2 m} \sum_{v} k_{v} \delta\left(c_{v}, i\right)$, and the proportion of edges linking vertices in community 𝑖 to
those in community 𝑗 is denoted by: $e_{i j}=\frac{1}{2} \sum_{u v} \mathrm{~A}_{u v} \delta\left(c_{u}, i\right) \delta\left(c_{v}, i\right)$. Consequently, the
variation in Q when two communities i and j merge is given by:
ΔQij=eij+eji–2aiaj.
Considering an iterative algorithm approach, let us assume a sparse matrix that encapsulates Δ𝑄𝑖𝑗 for each pair of communities 𝑖 and 𝑗 that are connected by at least one edge. Within the matrix Δ𝑄𝑖𝑗, the max-heap 𝐻 holds the maximum value from each row along with the labels 𝑖 and 𝑗 of the respective community pair. We then apply GMM (See Algorithm 1), which aims to optimize modularity (Asif & Islam, 2016; Harris et al., 2023). This objective is to recognize a division of nodes that maximizes the internal edges of communities compared to an expected result in a random arrangement.
Figure A1. Communities and Sub-communities detected sequentially by GMM. The left sub-figure represents the result of the first detection on the collaboration network. The middle one is the community detected with most awardees in the first detection. The right one is network structure of one community in the second detection. The huge circle represents awardees, and the color indicates the sub-field of mathematicians. |
2.2 Infomap based on Map equation
Rosvall et al. (2009) introduced an innovative method that relies on random walks, a concept where a walker transitions between nodes stochastically to analyze information flow in a network. The key idea of the Infomap algorithm is to find the most compact description of the network’s structure. This is achieved by encoding paths of random walks to reflect the network’s community structure. The algorithm iteratively tests different network partitions to reduce the required information to describe the random walker’s trajectory. Through this process, it detects tight-knit communities with rich information exchange.
Infomap (Algorithm 2) cluster nodes together which facilitate quick and efficient information exchange, forming well-defined modules. The connections between these modules represent the channels along which information moves. The Map Equation, central to this method, is presented as follows:
$\begin{aligned} L(\boldsymbol{M}) & =q_{\curvearrowright} \boldsymbol{H}(\mathcal{Q})+\sum_{i=1}^{m} p_{\circlearrowright}^{i} \boldsymbol{H}\left(\mathcal{P}^{i}\right), \\ & =\left(\sum_{i=1}^{m} q_{i \curvearrowright}\right) \log \left(\sum_{i=1}^{m} q_{i \curvearrowright}\right)-2 \sum_{i=1}^{m} q_{i \curvearrowright} \log \left(q_{i \curvearrowright}\right)-\sum_{\alpha=1}^{N} p_{\alpha} \log \left(p_{\alpha}\right)+\sum_{i=1}^{m}\left(q_{i \curvearrowright}+\sum_{\alpha \in i} p_{\alpha}\right) \log \left(q_{i \curvearrowright}+\sum_{\alpha \in i} p_{\alpha}\right) \end{aligned}$
where $q_{\curvearrowright}$ symbolizes the chance of a random walk transitioning between modules at any step, H(Q) is the entropy reflecting the randomness in module switching, H(Pi) accounts for the entropy of movements within a module, and pα is the frequency at which a node α is visited in the steady state of the random walk. The term $q_{i \curvearrowright}$ denotes the likelihood of the random walker leaving module i per step, and the sum of $p_{\circlearrowright}^{i}$ across all modules equals $1+q_{\curvearrowright}$, balancing the equation.
3 Comparative evaluation
In the sphere of community detection, it is vital to assess the algorithms based on their ability to mirror the structural cohesion seen in real-world groups. This endeavor requires metrics that can measure the congruity between identified communities by algorithms and the actual observed groupings. A widely recognized metric for this purpose, introduced by Danon et al. (2005), is the Normalized Mutual Information (NMI). This metric evaluates the shared information between the true classification of community memberships and that uncovered by community detection algorithms, taking account of the size of each grouping.
Consequently, NMI offers a standardized accuracy gauge in reflecting the authentic community structure. It is a robust tool for gauging and contrasting the efficacy of various algorithms in discerning significant community formations in networks.
At the heart of this metric is the confusion matrix P, where “real” communities constitute the rows and “detected” communities form the columns. An element 𝑃𝑖𝑗 within this matrix represents the count of nodes from actual community 𝑖 identified in detected community 𝑗. Deriving from principles of information theory, NMI is computed as follows:
$I(A, B)=\frac{-2 \sum_{i=1}^{C_{A}} \sum_{j=1}^{C_{B}} P_{i j} \log \left(\frac{P_{i j} P}{P_{i \cdot} P_{. j}}\right)}{\sum_{i=1}^{C_{A}} P_{i \cdot} \log \left(\frac{P_{i \cdot}}{P}\right)+\sum_{i=1}^{C_{B}} P_{\cdot j} \log \left(\frac{P_{. j}}{P}\right)}.$
The variable CA signifies the number of real communities, CB is the number of detected communities, 𝑃𝑖⋅ symbolizes the summation over row 𝑖 of the matrix Pij, and P⋅j stands for the summation over column j. An NMI value of 1 implies perfect alignment between the detected and actual communities. On the other hand, an NMI of 0 indicates no correspondence, such as when an algorithm fails to differentiate any distinct communities and groups the entire network as a single community.
Acknowledgement
We thank OpenAlex for the scientific corpus dataset. The computation in this study was supported by the Center for Computational Science and Engineering of the Southern University of Science and Technology.
Funding information
This work was supported by grants from the National Natural Science Foundation of China No. NSFC62006109 and NSFC12031005, the 13th Five-year plan for Education Science Funding of Guangdong Province No. 2021GXJK349, No. 2020GXJK457, and the Stable Support Plan Program of Shenzhen Natural Science Fund No. 20220814165010001.
Data availability statement
The data are mainly collected from the open data resources-OpenAlex (https://openalex.org/), and the supplementary awardees’ information is available from the corresponding author upon reasonable request.
Author contributions
Yurui Huang (12031320@mail.sustech.edu.cn): Conceptualization (Lead), Data curation (Equal), Formal analysis (Lead), Software (Lead), Visualization (Lead), Writing - original draft (Lead).
Zimo Wang (sdheitu@yeah.net): Data curation (Equal), Formal analysis (Supporting), Software (Supporting), Writing - review & editing (Supporting).
Chaolin Tian (12131250@mail.sustech.edu.cn): Investigation (Supporting), Validation (Supporting), Writing - review & editing (Supporting).
Yifang Ma (mayf@sustech.edu.cn): Funding acquisition (Lead), Methodology (Equal), Project administration (Lead), Validation (Lead), Writing - review & editing (Equal).