1 Introduction
The field of social network analysis (SNA) has evolved significantly over the past 50 years, being highly fragmented in the 1970s, forming an invisible college of its representatives in the 1990s, and facing the “invasion of the physicists” and development of network science in the 2000s (Bonachich, 2004; Freeman, 2004; 2011; Hummon & Carley, 1993). The number of studies showed a clear division of the field into two main subgroups (Batagelj et al., 2020; Brandes & Pich, 2011; Kejžar et al., 2010), and only recently did representatives of the two streams officially meet at the joint Sunbelt and NetSci Conference Networks 2021. Currently, the field is represented not only by scholars from “traditional” disciplines, but also many others, including neuroscience, medicine, and animal SNA in behavioral biology (Maltseva & Batagelj, 2019), which attracts the attention of researchers to the study, knowledge structuring, and reflection on the current development of this field.
This paper is a continuation of a project exploring the current state of the SNA field, which results have already been partly presented in previous articles (Maltseva & Batagelj, 2019, 2020, 2021, 2022). The project analyzes data on publications of authors writing articles on SNA (sourced from Web of Science indexed journals, comprising 70,792 articles up to 2018). Previously, we extracted the most important works in the field and examined discipline development through the analysis of citations between works (Maltseva & Batagelj, 2019), described the most represented topics based on the analysis of keyword co-occurrence (Maltseva & Batagelj, 2020), determined the groups of most important journals through their citation patterns (Maltseva & Batagelj, 2021), and observed the collaboration trends and structures of scholars involved in SNA based on their co-authorship (Maltseva & Batagelj, 2022).
In the present study, we employed two citation-based metrics, direct citation and bibliographic coupling, to analyze the structure of the scientific community of SNA scholars. We follow the approach to bibliometric network analysis presented in previous papers (Batagelj et al., 2014; Batagelj et al., 2017; Batagelj et al., 2020; Kejžar et al., 2010; Maltseva & Batagelj, 2019, 2020, 2021, 2022), including the temporal quantities approach proposed to study temporal networks (Batagelj & Maltseva, 2020; Batagelj & Praprotnik, 2016). To study scholarly networks, we combined the analysis of social networks, where a node is a social actor (an author), and information (citation) networks, where a node is usually an artifact (Yan & Ding, 2012a). We operationalize the citing relation “x cites y” as the work y appears in the list of references of the work x. We combined the information on citations between works with the authorship information linking authors to works for constructing the networks of author citation and author bibliographic coupling, which links authors according to direct citations and similarity of their citation practices.
The analysis of the citation-based networks of authors can bring important results to the understanding of the current development of a scientific discipline and identify the groups of tightly connected authors or their invisible colleges (Price, 1963). The combination of citation networks based on real connections and similarity measures allows conclusions to be drawn on how the structures coincide. Our research questions are attributed to three levels used to study scholarly networks (Yan & Ding, 2012a):
● Macro-level: What are the global structural features and trends of citations between the authors in SNA?
● Meso-level: What groups of authors can be detected in SNA according to their direct and indirect citation patterns?
● Micro-level: Who are the most prolific authors in SNA based on citation analysis, and how does their individual behavior change over time?
Having in mind the “tension” between social and natural branches of network analysis, which historically originated during the formation of the discipline and its community, we believe it is important to study the current state of SNA development. For all the scientists working with networks, it could be profitable to discuss the field’s development not in a discourse of “invasions”, but in terms of common collaboration and awareness of each other’s work. Looking at the field of SNA from different perspectives can provide us with the information on the overall development of the scientific community, detect different scientific schools, invisible colleges (Price, 1963), or author citation clubs (Brandes & Pich, 2011), and find some “centers of attention” around which the field could be formed, tracing the integration tendencies within the community.
Citation network analysis was previously applied to the studies of SNA development at the level of works and journals (Batagelj et al., 2014; Batagelj et al., 2020; Brandes & Pich, 2011; Chen, 2005; Hummon & Carley, 1993; Kejžar et al., 2010; Lazer et al., 2009; Leydesdorff et al., 2008; Maltseva & Batagelj, 2019). The analysis of citation networks was also conducted for literature in the complex networks (Shibata et al., 2007, 2008, 2009) and small world (Garfield, 2004) domains. The majority of studies that considered the groups of authors in SNA were either historiographically oriented (Freeman, 2004, 2011; Hidalgo, 2016) or analyzed collaborations between researchers based on co-authorship (Batagelj et al., 2014; Batagelj et al., 2020; Kejžar et al., 2010; Leydesdorff et al., 2008; Lietz, 2009; Maltseva & Batagelj, 2022; Otte & Rousseau, 2002). The analysis of structures of citation and bibliographic coupling at the author level is much rarer (Batagelj et al., 2020; Brandes & Pich, 2011; Kejžar et al., 2010), which emphasizes the importance of the current study.
The remainder of this paper is organized as follows. Section 2 provides the grounds for studying author citation networks and presents previous studies of citation and bibliographic coupling structures among the authors in SNA. Section 3 describes the dataset and some issues of network construction (including temporal networks) from the original networks of citations between works and the two-mode authorship network connecting works with authors. Section 4 presents the results: the general trends of citations, the most cited and citing authors, and the groups of authors extracted based on the analysis of the citation and bibliographic coupling structures. We use temporal versions of some of the networks to gain insight into the dynamics of these relationships.
2 Author citation analysis
2.1 Citation analysis as a tool for studying science
Citations are understood as important mediums and abstract codes (Leydesdorff, 1998), or “concept symbols” (Small, 1978), of scientific communication. The reasoning first applied to the analysis of citation networks of scientific papers (Garfield, 1955, 1971; Garfield & Merton, 1979; Price, 1965) was later proposed to be used for the analysis of other bibliographic units, such as authors or journals (Garfield, 1972; Rice et al., 1989). Citation analysis, as a substantive research area specializing in the statistics of citations in publications and an analysis of citation networks (Marshakova-Shaikevich, 2013), has been shown to be capable of revealing patterns of development in science, identifying its disciplinary structure and emerging research areas, its social and cognitive aspects, and conducting a quantitative assessment of scientific research. Some challenges of citation network analysis relate to the meaning of citations and associated metrics, as it has been shown that there are different social, psychological, and normative aspects and no single theory of citations (Leydesdorff, 1998; Smith, 1981), and their (mis)interpretation as a measure of a scientific impact (Hicks et al., 2015; Szomszor et al., 2020). Certain concerns are related to a phenomenon of self-citation (self-mentioning): used strategically, it can lead to excessive, extreme self-citations, gained through the citation “farms” and “cartels”, relatively small clusters of authors massively citing each other’s papers (Ioannidis et al., 2019). However, scholars agree that researchers have legitimate reasons to cite their own work or the work of their coauthors, and this demonstrates how much (the group of) authors draws upon their own work to inform their current work (Szomszor et al., 2020).
Within citation analysis, there are different approaches to scholarly network construction and analysis. Networks of a direct citation belong to the “real connection-based networks” type of scholarly networks, as defined by Yan and Ding (2012a). Citation counts represent the perceived utility or impact of scientific work, as determined by the corresponding scientific community (Garfield & Merton, 1979). The relations in the networks of the second type, “similarity-based networks”, are formed by the similarity measures between documents. Citation-based similarity measures can be formed into two dimensions: being cited by other works (receiving acknowledgment from another document) and citing other works (giving acknowledgment to another document), creating co-citation and bibliographic coupling networks. Co-citation (Marshakova, 1973; Small, 1973) defines a single item of citation made for two papers as a unit of coupling between them and measures the link between the two papers as the number of documents in which both papers are cited simultaneously. It is the frequency with which two items of earlier literature are cited together by later literature. Bibliographic coupling (Kessler, 1963) defines a single item of reference used by two papers as a unit of coupling between them and measures the link between two papers as the number of common cited documents. It is the frequency with which the two items of the later literature both cite an earlier paper. Two documents are bibliographically coupled if their reference lists share one or more of the same cited documents, and they are co-cited if they appear in the same reference list. In some sense, both methods are dual to each other, but have important differences (Marshakova, 1981; Small, 1973): the strength of bibliographic coupling of two papers does not change with time, while it may change for co-citation. Each type of citation network analysis can employ different counting and weighing algorithms.
As well as with the direct approach, similarity measures based on co-citation and bibliographic coupling were later proposed for journals (Boyack et al., 2009; McCain, 1991; Small & Koenig, 1977) and authors (White & Griffithi, 1981; White & McCain, 1998; Zhao & Strotmann, 2008). Among these three methods, co-citation analysis is claimed to be the most commonly used and well-known literature-based technique for studying the intellectual structure of scholarly fields and the characteristics of scholarly communities (Zhao & Strotmann, 2015). According to Zhao and Strotmann (2008), bibliographic coupling has rarely been applied to knowledge-network analysis as an indicator of relatedness between documents due to the difficulty of retrieving information directly from the databases provided by the Institute for Scientific Information (ISI). However, Zhao and Strotmann (2008) noted several limitations of author co-citation analysis and showed that this approach better shows the structure of intellectual impact on a field as perceived by its active authors (influence on the field). The authors proposed author bibliographic coupling analysis as a method of mapping active authors of a field, which provides a more realistic picture of research activities. According to their approach, the overlap of all references cited by the two authors can be regarded as their bibliographic coupling strength. An alternative approach based on counting bibliographic coupling for articles first, and then to authors, was proposed by Leydesdorff (Yanhui et al., 2021). Recent developments in this approach combine bibliographic coupling information with other types of data (for example, Zhang and Yuan (2022) using semantic and syntactic citation information).
With the variety of scholarly citation-based networks, some studies have raised the question of comparison between them (Boyack & Klavans, 2010; Shibata et al., 2009; Yan & Ding, 2012b). Studying the intellectual structure of the information science (IS) field during the period 1996-2005 (WoS data, in 12 core IS journals), Zhao and Strotmann (2008) concluded that two observed citation-based author-mapping methods (author co-citation and bibliographic coupling analyses) complement each other and provide a more comprehensive view of the intellectual structure of the IS field in combination than each of them can provide on its own. Yan and Ding (2012b) found high similarity between co-citation and citation networks, as well as bibliographic coupling and co-citation networks. Gazni and Didegah (2016) examined the association between author bibliographic coupling strength and citation exchange in 18 subject areas and found a positive and significant correlation between the two factors.
At the same time, scientometric studies are largely focused on paper citation dynamics, and author citation dynamics have received little attention in the literature. On the empirical level, it can be due to the challenges related to author name disambiguation, and on the theoretical side, to the fact that our understanding of citation accumulation for papers could be leveraged to characterize and model the citation dynamics of authors (Silva et al., 2020). Recent analyses show that the citation distribution follows a power law, and its tail, capturing the number of high-impact papers, is generated through a cumulative advantage process or preferential attachment, suggesting that the probability of citing a paper grows with the number of citations that it has already collected (Fortunato et al., 2018). These generative mechanisms driving the accumulation of citations can also be used to explain the citation dynamics of authors and even to predict their citations in the future (Silva et al., 2020).
Research using these methods is usually focused on the study of specific scientific fields and usually reveals the relevant relations between authors and maps a more detailed domain intellectual structure. Below, we proceed with the results of citation analysis for studying SNA literature and field representatives.
2.2 Author citation analysis for studying SNA
While the majority of studies have analyzed the structures of authors in the field of SNA based on their collaboration structures (and their overview is presented in Maltseva and Batagelj (2022)), there are only a few examples of citation network analysis applied to network scholars. These studies implemented methods of aggregated direct citation network analysis between authors and bibliographic coupling among them.
The analysis of citations between authors from the field of clustering and classification (WoS, 1970-2008) by Kejžar et al. (2010) identified a large number of subgroups in the authors’ citation network joining the larger group, which indicated a single main topic in the network. Batagelj et al. (2020) studied the citation structures among authors in the research domain on network clustering and blockmodeling (WoS, descriptions of articles till February 2017). The authors identified 16 subgroups of the most connected scholars. One of them, the community detection island, was large and massively centered on the representatives of network science Newman, Fortunato, Barabási, Albert, and Girvan. The island containing publications of social scientists on blockmodeling was smaller and less centralized, with Doreian being the most central author, connected to Batagelj and Ferligoj (works on blockmodeling), Mrvar (signed networks), Brusco and Steinley (algorithms for partitioning networks). This cluster also includes groups of Borgatti and Everett, as well as Robins, Pattison and Wasserman, all prominent in SNA, which means that this island is on the topic of blockmodeling.
Several studies used the bibliographic coupling approach to SNA data (Batagelj et al., 2014; Batagelj et al., 2020; Brandes & Pich, 2011; Lazer et al., 2009); however, it was extended to authors only in a few of them. Analyzing direct citation and bibliographic coupling between the authors in SNA (the dataset SN5 by Batagelj (2008), WoS, descriptions of articles on social networks till 2007), Brandes and Pich (2011) identified the authors with the largest number of citations received (Granovetter, Berkman, Wasserman, Burt, Cohen, House, Coleman, and Freeman). Some of these authors (such as Wellman) occupy a peripheral position in the bibliographic coupling network due to their distinct specialties or larger range of diversity. Only two parts of the network formed visible clusterings: the group of authors working on health-related issues and the network science group, where the coupling among authors was much stronger. Brandes and Pich (2011) conclude that these clusters in the coupling network could be due to the “citation culture in the field, or author citation clubs”. Applying the bibliographic coupling approach to the authors in clustering literature, Batagelj et al. (2020) extracted two disjoint groups of authors, where the smaller group included authors from SNA active in blockmodeling centering Doreian, and the larger group included researchers from the physics driven literature centering Newman.
According to these findings, citation analysis can extract groups of authors more closely connected to each other than to other authors in the area of SNA due to their affiliation with various disciplines. Most notable is the division of authors into social sciences and network science, which has been identified in previous studies. In the social sciences, there is also a division of researchers into groups based on the topics and methods they develop. The obtained groups are represented by the key scholars in the SNA field, its founding fathers and mothers, who form the core of the discipline. To a certain extent, the results obtained are related to the analyzed data, whether papers from the social sciences (Brandes & Pich, 2011) or different related subject areas (Batagelj et al., 2020; Kejžar et al., 2010) are considered. Through the analysis of a large and complete dataset, we expect to reveal a more detailed division of scholars from SNA into subgroups. Besides the groups of authors, our analysis also shows the global structural features of citations between the authors, as well as the most prolific authors and their individual behavior, including changes in time. By presenting the overall analysis of the authors’ citation structures in the field of SNA, our study extends and improves the findings of previous research.
3 Data
3.1 Data collection
The dataset consists of articles from the WoS database WoS Core Collection, Clarivate Analytics’s multidisciplinary database of bibliographic information containing over 21,100 peer-reviewed, high-quality scientific journals published worldwide in over 250 areas of science, including social sciences and humanities (Web of Science, 2023). Previous comparisons of different databases of bibliometric data, such as Scopus, Google Scholar, and special citation resources and scientific social media, such as SciFinder and Mendeley, have shown that they vary significantly according to their coverage of certain scientific disciplines and have their pros and cons. The WoS contains mainly publications from journals with a certain impact factor and provides coverage back to 1,900 with bibliometric descriptions including references. Its higher consistency and accuracy of data, cover-to-cover indexing of the journals, and availability of references in bibliographic descriptions made the choice of the WoS most appropriate for the current study.
The initial dataset was formed from the publications matching the query “social network*”, and thus some works related to the broader field of network analysis could have been overlooked. The search query for “network analysis” would be too broad, including the works on computer networks, optimization problems for networks, etc. We used an iterated saturation search of papers that were intensively cited in the initial dataset but did not have full descriptions as the main approach to discover important papers overlooked by the initial query. We searched for the works with high (at least 150) citation frequencies using WoS. If a description of a work was not available in WoS, we constructed a corresponding description without CR data and searched for the work using Google Scholar. We also extended the results of the original query with papers published by the most prominent authors (around 100 scholars) and works from flagship SNA journals indexed in WoS (such as Social Networks, Network Science, Social Network Analysis and Mining, and Journal of Complex Networks). Other network-related journals, such as Computational Social Networks, Applied Network Science, Online Social Networks and Media, Journal of Social Structure, and Connections, were considered, but were not abstracted in the WoS. The used strategy resulted in the dataset, which covers not only the works of social scientists, but also influential papers published by physicists, biologists, information and computer scientists, etc. Previous analyses on this dataset (Maltseva & Batagelj, 2019, 2020, 2021, 2022) show that the strategy we used was appropriate to extract expected sample data, and this approach produces a good coverage of the field’s important publications. We should note that other strategies of data collection could be used, such as using other relevant keywords extracted from SNA journals and controlled vocabularies; this information can now be taken from the results of this project. To be consistent with our other studies, we had to stick to working on the dataset collected up to 2018.
To transform the data into a collection of linked networks, the WoS2Pajek 1.5 program (Batagelj, 2017) was used. This resulted in a one-mode citation network Cite on works (from the field CR of WoS article description (Web of Science, 2023)) and a two-mode authorship network WA on works × authors (from the field AU), used in the current analysis. Works can be of two types: with full descriptions (hits), and cited only (terminal, only listed in CR field). For terminal publications that were frequently cited, we additionally searched for complete descriptions with or without references. The work’s description (record) from WoS is semi-structured, and the process of entity resolution is dependent on the solutions provided in the program WoS2Pajek and manual improvements.
For work names, we used the short names of the following format: LastNm [:8] + “_’’ + FirstNm [0] + “(” + PY+ “)” + VL + “:” + BP (author’s last name and first initial, year of publication, volume, beginning page). For example, GRANOVET_M (1985)91:481. For last names with prefixes the spaces are deleted, and unusual names start with characters * or $. The names of the authors are encoded by the first eight characters of their surnames and the first initials of their first names, as in GRANOVET_M. With this approach, some problems with author name recognition can occur. It is possible that the same work is named using different short names. For example, the short names BOYD_D (2007)13 and BOYD_D (2008)13:210 referencing the same work of Danah Boyd, were originally published in 2007, but in many cases referenced as being published in 2008. There were also cases when the short names were different due to the discrepancies in the descriptions, such as GRANOVET_M (1973)78:1360 and GRANOVET_M (1973)78:6, or COLEMAN_J (1988)94:95 and COLEMAN_J (1988)94: S95. Accordingly, the names of some authors were presented in a different way, for example, GRANOVET_M and GRANOVET_.
To resolve these problems, we have to correct the data. There are two possibilities: (1) to make corrections in the local copy of the original data (WoS file) and (2) to make an equivalence partition of nodes and shrink the set of works accordingly in all obtained networks. We used the second option (Batagelj et al., 2014). For works with large frequencies, we prepared lists of possible equivalents and manually determined equivalence classes. With a function in R, we produced Pajek’s partition of equivalent work names representing the same work. We used this partition to shrink the networks Cite and WA accordingly (Batagelj et al., 2014).
Another problem is author disambiguation, when different authors have the same name, well-known in the literature as the problem of “multiple personalities” (Harzing, 2015). It is especially relevant for authors with Chinese and Korean names due to the “three Zhang, four Li” effect, but can occur also with authors with common surnames (e.g. Smith, Rodriguez, Johnson). In the previous analysis of coauthorship (Maltseva & Batagelj, 2022), a set of Chinese/Korean authors popped up in the results as the most productive authors. For authors with such names, the solution of WoS2Pajek does not perform well, as it does not yet support multi-personality resolution: different authors, having the same surname and first initial of their first name, merge during the creation of the network WA.
The corrections can be done manually, if necessary, on critical units after the inspection of the results. We checked the obtained results carefully and in case that some error pops up, we appropriately corrected the data and rerun the analyses. As researchers involved in the field of network analysis for many years, we know which researchers with Chinese/Korean names significantly contributed to the field. To deal with the multi-personality problem, we removed the other authors with Chinese/Korean names from the obtained results, they were included in the analysis. In Appendix A, we show that the results for correctly identified authors are not affected by multi-personalities. In the future, we could solve this problem using a single universal ID for each author (as ORCID). In addition to unit names, some bibliographic databases provide their unique identifiers (DBLP, MathSciNet, Scopus, OpenAlex) (Baas et al., 2020; DBLP, 2024; OpenAlex, 2024; TePaske-King & Richert, 2001), making the construction of networks much easier, but this information is often missing in WoS descriptions. We believe that the disambiguation of all kinds of bibliographic units (authors, works, institutions, journals, etc.) should be performed in bibliographic databases. We can consider this issue of authors disambiguation and multiple personalities as a limitation of the study, which is based on information from the WoS database. However, as we show, these problems do not significantly influence the results.
From 70,792 hits, we produced networks with |W| = 1,297,133 works and |A| = 395,971 authors. Multiple links and loops were removed. The obtained basic networks were labeled CiteN and WAn. As for terminal publications, only information on the first author was provided. For our analysis, we constructed reduced networks on works with complete descriptions CiteR and WAr, with the following set sizes: works |W| = 70,792, authors |A| = 93,011. We used these reduced networks in our analysis.
3.2 Derived networks
Using multiplication of networks (for details see Batagelj, 2020a; Batagelj & Cerinšek, 2013; Batagelj et al., 2014), we constructed derived networks. Combining the citation network Cite with the authorship network WA, we produced three types of derived networks. First, the network of citations of works to authors CiA, where the weight CiA[w,a] of the arc (w,a) counts the number of times the work w cited the author a. Second, the network of citations among authors ACiA, where the weight ACiA[a,b] of arc (a,b) counts the number of times author a cited author b. Third, the network of bibliographic coupling between authors ACoj, where the weight of the edge between two nodes measures the similarity of author citation patterns. By normalizing the weights of the links in basic networks, the derived networks can be normalized.
3.3 The normalization of derived networks
Let us consider the network Cite, where each work (node) has a different number of references. Through normalization, we create a network n(Cite), where the weight of each arc is divided by the sum of the weights of all arcs having the same initial node as this arc (the outdegree of a node) (Batagelj & Cerinšek, 2013).
$ n(\text { Cite })[u, v]=\frac{\text { Cite }[u, v]}{\max \left(1, \text { outdeg }_{\text {Cite }}(u)\right)}$
For N(u) ≠ ∅ it holds ΣvϵN(u) n(Cite)[u,v] = Cite[u,v] = 1.
In a similar way, we normalize the network WA. Normalization creates a network n(WA), where the weight of each arc is divided by the sum of the weights of all arcs having the same initial node (outdegree of a node) (Batagelj & Cerinšek, 2013).
$ n(\mathbf{W A})[w, a]=\frac{\text { WA }[w, a]}{\max \left(1, \text { outdeg }_{\mathbf{W A}}(w)\right)}$
These normalized networks were used for the construction of the normalized derived networks.
3.4 Networks of citations
To obtain information about citations of works to authors, we computed the network CiA as a product of the networks Cite and WA:
$ \mathbf{C i A}=\mathbf{C i t e} * \mathbf{W A}$
The weight CiA[w,a] counts the number of citations of work w to author a. The indegree indegCiA(a) of author a in the network CiA is equal to the number of works citing author a, and the weighted indegree windegCiA(a) of author a in this network is equal to the total number of appearances of author a in all lists of references.
We considered two fractional versions of this network
$ \mathbf{C i A}^{\prime}=\mathbf{C i t e} * n(\mathbf{W A})$
and
$ \mathbf{C i A}^{\prime \prime}=n(\mathbf{C i t e}) * n(\mathbf{W A})$
For the network CiA″, which is used in the further analysis, the indegree distribution, number of works citing the author, is the same as for the network CiA (indegCiA(a) = indegCiA′′(a)). However, the values of weighted indegree are different: windegCiA′′(a) of an author a in the network CiA″ is equal to the fractional contribution of citations to the author a.
For a network N = (V, L, w), we define its total weight as
$ T(\mathbf{N})=\sum_{(u, v) \in L} w(u, v)$
It is easy, see Appendix B, to verify that
$ T\left(\mathbf{C i A}^{\prime}\right) \leq\left|L_{\text {Cite }}\right|$
each reference in the network Cite has value 1 that is distributed among authors; and
$ T\left(\mathbf{C i A}^{\prime \prime}\right) \leq\left|W_{\text {Cite }}^{+}\right| \leq|W|$
each work in the network Cite with at least one reference has value 1 that is distributed among authors:
$ W_{\text {Cite }}^{+}=\left\{w \in W: \text { outdeg }_{\text {Cite }}(w)>0\right\}$
Similarly, we get the network ACi of citations of authors to works
$ \mathbf{A C i}=\mathbf{W A}^{T} * \text { Cite }$
with its fractional versions ACi′ = n(WA)T ∗ Cite and ACi′′ = n(WA)T ∗ n(Cite).
To obtain information about citations among authors, we computed the network ACiA as a product of the networks WA and Cite.
$ \mathbf{A C i A}=\mathbf{W A}^{T} * \text { Cite } * \mathbf{W A}$
In this network, the value of the element ACiA[a,b] is equal to the number of citations from works co-authored by a to works co-authored by b: how many times author a cited author b. The value of the element ACiA[a,a] (loop) is equal to the author’s self-citation. Having information on the number of works for each author, indegWA(a), it is possible to compute the authors’ average self-citation as ACiA[a,a] / indegWA(a).
Using the fractional approach, we also produced normalized versions of this network with weights expressing the fractional contribution of citations given by an author to another author.
$ \mathbf{A C i A}^{\prime}=n(\mathbf{W A})^{T} * \mathbf{C i t e} * n(\mathbf{W A})$
and
$ \mathbf{A C i A}^{\prime \prime}=n(\mathbf{W A})^{T} * n(\mathbf{C i t e}) * n(\mathbf{W A})$
Again, we have, see Appendix,
$ T\left(\mathbf{A C i A}^{\prime}\right) \leq\left|L_{\text {Cite }}\right|$
each citation has value 1 that is distributed among authors; and
$ T\left(\mathbf{A C i} \mathbf{A}^{\prime \prime}\right) \leq|W|$
each work with at least one author has value 1, which is distributed among authors.
In the network ACiA, the indegree indegACiA(a) of an author a is equal to the number of different authors citing the author a, and the weighted indegree windegACiA(a) of an author a is the total number of references to the author a from all authors. In the network ACiA″, indegree is the same as for the network ACiA (indegACiA(a) = indegACiA″(a)), but the weighted indegree windegACiA″(a) of an author a is equal to the fractional contributions of references from all authors to author a. The value of the element ACiA″[a,a] is equal to the author’s fractional self-citation.
3.5 Bibliographic coupling network
Bibliographic coupling occurs when two works reference a third work in their bibliographies, which suggests some content communality between these two works. Having more prior work referenced by a pair of later works increases their likelihood of sharing content (Batagelj et al., 2020). We used the network Cite to produce the network biCo, which can be determined as:
$ \text { biCo }=\text { Cite } * \text { Cite }^{T}$
biCo[p,q] = # of works cited by both works p and q = | Cite(p) ∩ Cite(q) |
Bibliographic coupling weights are symmetric: biCo[p,q] = biCo[q,p].
The fractional approach can be applied in different ways to obtain a normalized bibliographic coupling measure (Batagelj, 2020a, p. 12). Among them, we selected the Jaccard index.
$ \operatorname{biCoj}[p, q]=\frac{|\operatorname{Cite}(p) \cap \operatorname{Cite}(q)|}{|\operatorname{Cite}(p) \cup \operatorname{Cite}(q)|}$
We constructed the author bibliographic coupling network ACoj by multiplying biCoj with the normalized network n(WA). Weights in the obtained network take into account the fractional similarity of authors a and b.
$ \mathbf{A C o j}=n(\mathbf{W A})^{T} * \mathbf{b i C o j} * n(\mathbf{W A})$
The values of the links between works from biCoj are redistributed to links between authors in ACoj. The total sum of the link weights is preserved:
$ T(\mathbf{A C o j})=\sum_{e \in E(\mathbf{A C o j})} \mathbf{A C o j}[e]=\sum_{e \in E(\mathbf{b i C o j})} \mathbf{b i C o j}[e]=T(\mathbf{b i C o j})$
In the network ACoj, the loops were deleted, and the bidirected arcs were converted to edges (with a summation of values) before further analysis.
3.6 Temporal networks
Bibliographic datasets can also be approached using temporal hypergraphs (Ouvrard, 2017). In this study, we adhere to the traditional approach based on a collection of networks well supported by network analysis software. Applying the temporal quantities approach (Batagelj & Maltseva, 2020; Batagelj & Praprotnik, 2016) to the networks WA and Cite, we created several temporal networks, using libraries Nets and TQ in Python. The obtained networks are of two types: instantaneous WAins and CiteIns (with values per each year) and cumulative WAcum and CiteCum (with cumulative values over the years). The networks are stored in the JSON format.
By multiplication and normalization of the temporal networks, we created several derived temporal networks. First, we created the network TCiA, the temporal version of the network CiA, and its fractional version TCiA″:
$ \text { TCiA }=\text { CiteIns } * \text { WAcum }$
$ \mathbf{T C i A}^{\prime \prime}=n(\text { CiteIns }) * n(\text { WAcum })$
To observe the patterns of citations among authors through time, based on the temporal networks WAins, WAcum and CiteIns, we constructed two networks: regular TACiA and normalized TACiA″:
$ \text { TACiA }=\text { WAins }^{\mathbf{T}} * \text { CiteIns } * \text { WAcum }$
$ \mathbf{T A C i A}^{\prime \prime}=n({\mathbf{W A i n s})^{\mathbf{T}}} * n(\mathbf{\text { CiteIns } )} * n(\mathbf{\text {WAcum} )}$
In the obtained networks, the weight of the arc (a, b) equals to the number of citations / fractional contribution of citations given by author a to author b, through time.
4 Results
The description of the results is motivated by the research questions. We start with observing macro-level statistics of citations between the authors in the field of SNA. Then we move to the micro-level and show the most prolific authors in the field and their individual behavior, including the changes over time. Then, the results of the meso-level analysis are presented, showing the groups of authors that can be detected in the field under study.
4.1 Macro-level: Distributions of citations
In this subsection, we start with the macro-level analysis and present some statistics of citations between the authors in the field of SNA.
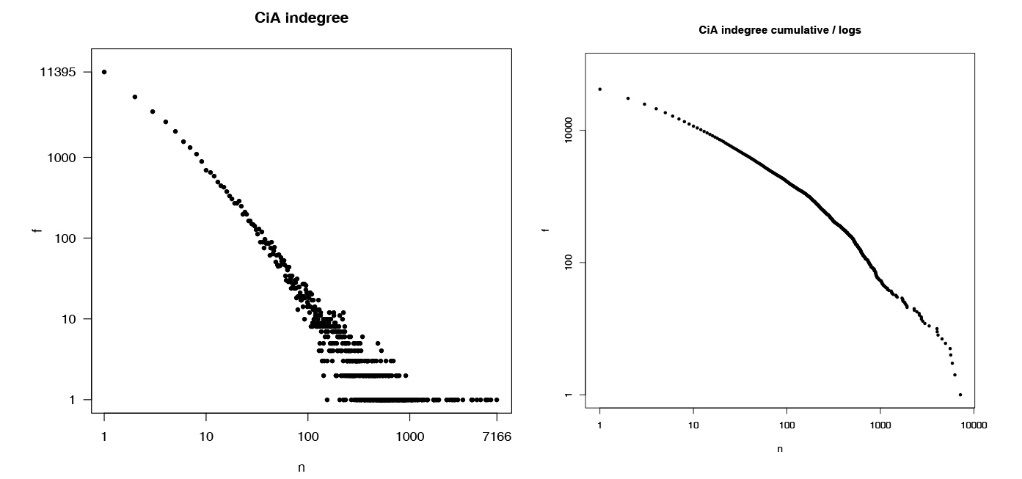
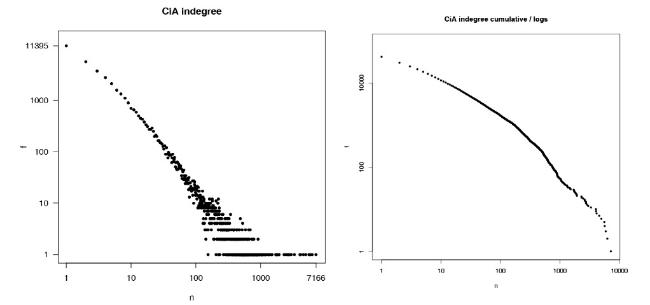
Figure 1. CiA: Indegree (number of citing works) distribution in double-logarithmic scale-frequency (left), and complementary cumulative (right). |
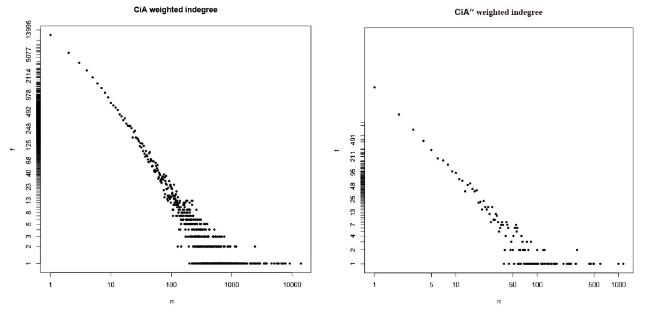
Figure 2. Weighted indegree frequency distribution: CiA/total number of citations (left) and CiA″/fractional contribution of citations (right). |
The density distribution of the authors’ average fractional self-citation from the network ACiA″ is shown in Figure 3. The value of average self-citation varies from 0 to 6.47; the average is 0.06 for all authors. For the majority of authors, the value of the average self-citation is either equal to 0 (87%) or is very low (0.1-0.3:5%, 0.4-0.7:5%, 0.8-1:1%). The peaks of the density are in values 1/2, 1/3, (1/4, 1/5, 1/6), 2/3, 1, etc. Only 797 authors have an average larger than 1. For a small group of authors, the values of the average self-citation are high. The top authors based on this measure are presented in the next subsection.
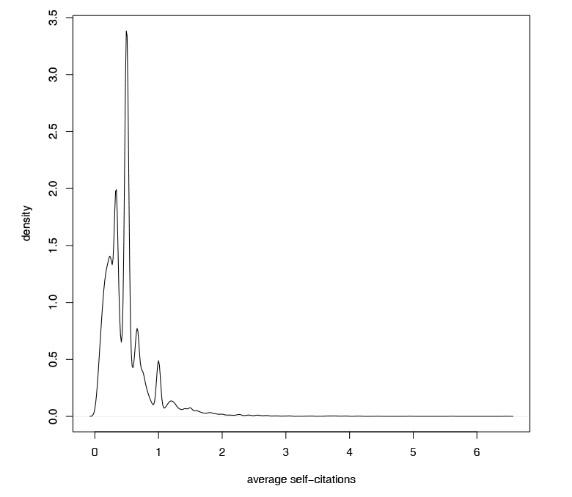
Figure 3. Authors’ average self-citation from ACiA″: density distribution. |
4.2 Micro-level: The most prolific authors
In this subsection, we move to the micro-level of analysis and present individual authors who are the most prolific. We investigate the top authors according to the indegree metric, that is, citations received by the author from other community members. We also use the metric of authors’ self-citations. Citation calculation is based on the subset of papers included in our dataset, that is, it shows the citations of the authors in SNA by other authors relevant for this field. However, we should keep in mind that SNA authors could be intensively cited by non-network researchers, and these values are not taken into account in our analysis.
Table 1. CiA and CiA″: The most cited authors. |
| # | CiA / CiA″ indegree | CiA weighted indegree | CiA″ weighted indegree | |||
|---|---|---|---|---|---|---|
| # | Value | Author | Value | Author | Value | Author |
| 1 | 7,166 | NEWMAN_M | 13,996 | NEWMAN_M | 1,143.9 | NEWMAN_M |
| 2 | 6,257 | GRANOVET_M | 9,131 | BARABÁSI_A | 996.3 | GRANOVET_M |
| 3 | 5,873 | WASSERMA_S | 7,762 | GRANOVET_M | 596.7 | BURT_R |
| 4 | 5,653 | FAUST_K | 7,371 | BURT_R | 497.7 | FREEMAN_L |
| 5 | 5,572 | BARABÁSI_A | 6,819 | WATTS_D | 490.9 | BARABÁSI_A |
| 6 | 4,966 | WATTS_D | 6,656 | WASSERMA_S | 456.3 | WASSERMA_S |
| 7 | 4,560 | BURT_R | 5,982 | FAUST_K | 452.2 | WATTS_D |
| 8 | 4,131 | FREEMAN_L | 5,791 | BORGATTI_S | 435.7 | FAUST_K |
| 9 | 4,047 | ALBERT_R | 5,649 | ALBERT_R | 309.4 | ALBERT_R |
| 10 | 4,028 | BORGATTI_S | 5,077 | FREEMAN_L | 308.6 | BOYD_D |
| 11 | 3,322 | STROGATZ_S | 4,562 | CHRISTAK_N | 299.9 | ELLISON_N |
| 12 | 2,984 | ELLISON_N | 3,802 | FOWLER_J | 295.6 | KLEINBER_J |
| 13 | 2,836 | KLEINBER_J | 3,747 | STROGATZ_S | 260.6 | BORGATTI_S |
| 14 | 2,743 | BOYD_D | 3,581 | ELLISON_N | 252.1 | ROGERS_E |
| 15 | 2,737 | CHRISTAK_N | 3,513 | SNIJDERS_T | 247.6 | CHRISTAK_N |
| 16 | 2,615 | SMITH-LO_L | 3,431 | KLEINBER_J | 241.5 | STROGATZ_S |
| 17 | 2,593 | MCPHERSO_M | 2,950 | BOYD_D | 232.2 | SCOTT_J |
| 18 | 2,454 | COOK_J | 2,887 | BRASS_D | 210.7 | FOWLER_J |
| 19 | 2,306 | FOWLER_J | 2,840 | GIRVAN_M | 174.4 | WELLMAN_B |
| 20 | 2,297 | GIRVAN_M | 2,778 | PATTISON_P | 167.2 | STRAUSS_A |
| 21 | 1,927 | SNIJDERS_T | 2,745 | SMITH-LO_L | 165.7 | FORTUNAT_S |
| 22 | 1,922 | EVERETT_M | 2,713 | MCPHERSO_M | 162.6 | GOFFMAN_E |
| 23 | 1,874 | JEONG_H | 2,534 | KRACKHAR_D | 161.1 | BOURDIEU_P |
| 24 | 1,836 | BRASS_D | 2,490 | FORTUNAT_S | 151.3 | GIRVAN_M |
| 25 | 1,815 | MARSDEN_P | 2,458 | COOK_J | 150.2 | PORTES_A |
| 26 | 1,748 | KRACKHAR_D | 2,425 | JEONG_H | 149.5 | MARSDEN_P |
| 27 | 1,734 | WELLMAN_B | 2,425 | WELLMAN_B | 140.3 | BANDURA_A |
| 28 | 1,725 | LESKOVEC_J | 2,364 | EVERETT_M | 137.7 | GIDDENS_A |
| 29 | 1,702 | FORTUNAT_S | 2,262 | MARSDEN_P | 137.2 | BERKMAN_L |
| 30 | 1,512 | SCOTT_J | 2,124 | ROBINS_G | 130.6 | WENGER_E |
| 31 | 1,480 | ROGERS_E | 2,114 | VALENTE_T | 124.4 | BONACICH_P |
| 32 | 1,465 | VALENTE_T | 2,078 | LESKOVEC_J | 123.1 | DAVIS_F |
| 33 | 1,371 | CROSS_R | 2,004 | CROSS_R | 122.8 | RADLOFF_L |
| 34 | 1,340 | UZZI_B | 1,803 | BERKMAN_L | 119.0 | KRACKHAR_D |
| 35 | 1,323 | VICSEK_T | 1,708 | UZZI_B | 118.5 | UZZI_B |
| 36 | 1,314 | BERKMAN_L | 1,636 | HANDCOCK_M | 117.9 | SNIJDERS_T |
| 37 | 1,305 | PATTISON_P | 1,629 | DUNBAR_R | 114.8 | ADOMAVIC_G |
| 38 | 1,232 | CLAUSET_A | 1,592 | ROGERS_E | 114.3 | EVERETT_M |
| 39 | 1,195 | BONACICH_P | 1,582 | KILDUFF_M | 112.3 | VALENTE_T |
| 40 | 1,189 | TSAI_W | 1,565 | TSAI_W | 103.4 | SMITH-LO_L |
| 41 | 1,183 | FALOUTSO_C | 1,540 | SCOTT_J | 101.4 | MCPHERSO_M |
| 42 | 1,141 | ADAMIC_L | 1,529 | BONACICH_P | 100.0 | LESKOVEC_J |
| 43 | 1,124 | ROBINS_G | 1,513 | JAMES_R | 99.7 | JENKINS_H |
| 44 | 1,105 | LAMBIOTT_R | 1,502 | STEGLICH_C | 98.4 | LIN_N |
| 45 | 1,081 | WANG_Y | 1,471 | VICSEK_T | 96.8 | KAPLAN_A |
| 46 | 1,068 | MEHRA_A | 1,395 | LIN_N | 96.2 | HAENLEIN_M |
| 47 | 1,060 | BARTHELE_M | 1,376 | CROFT_D | 95.5 | COOK_J |
| 48 | 1,046 | LIN_N | 1,375 | FALOUTSO_C | 91.0 | CORBIN_J |
| 49 | 1,039 | KILDUFF_M | 1,370 | WANG_Y | 90.0 | COHEN_S |
| 50 | 1,035 | LAZER_D | 1,289 | DAVIS_F | 86.9 | FISCHER_C |
Based on Table 1 , we selected eight top authors: Newman, Granovetter, Burt, Freeman, Barabási, Wasserman, Watts, and Faust. Using the network ACi, we found the most cited works of these researchers. These are “Social network analysis: Methods and applications” by Wasserman and Faust (cited by 9,469 authors), “The strength of weak ties” by Granovetter (7,737 authors), “Collective dynamics of ‘small-world’ networks” by Watts and Strogatz (5,383 authors), “Centrality in social networks: Conceptual clarification” by Freeman (4,924 authors), “Emergence of scaling in random networks” by Barabási and Albert (4,722 authors), “Structural holes: the social structure of competition” by Burt (3,807 authors), and “The structure and function of complex networks” by Newman (3,217 authors).
For these authors, we examined the temporal distributions of the number of citations from works: indegree and weighted indegree of TCiA, and weighted indegree of TCiA″ networks. These are presented in Figures 4 and 5 , respectively. These distributions show that while some authors collect their incoming citations from works through the whole periods of their professional lifes (sociologists Burt, Granovetter, Freeman, Wasserman, Faust), other managed to obtain the maximum values of citations through relatively short periods of time (physicists Newman, Barabási, Watts). For some authors, such as Newman, Burt, and Barabási, the difference between the incoming regular and weighted degrees is relatively large, which shows that their names appear several times in the same reference lists of the citing works.
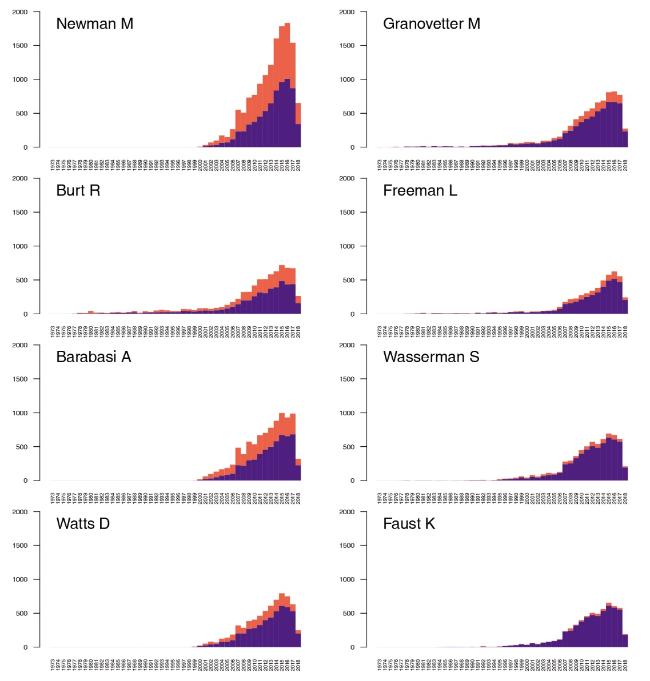
Figure 4. TCiA: Temporal indegree (purple/dark: number of citing works) and weighted indegree (red/light: number of references). |
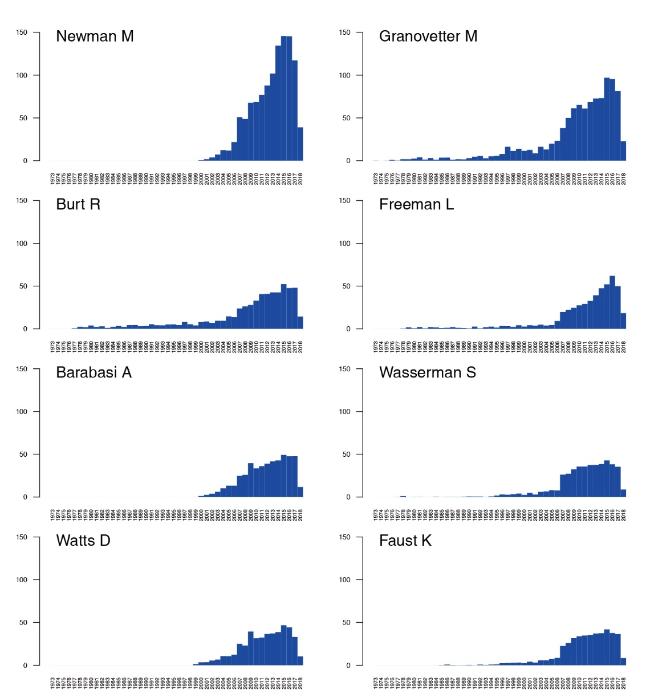
Figure 5. TCiA′′: Works citing authors: temporal weighted fractional indegree. |
For the selected top eight authors from Table 1 , we traced three similar measures, showing the temporal distributions of the numbers of citations from authors: indegree and weighted indegree of TACiA, and weighted indegree of TACiA″ networks. The distributions show citation trends similar to those observed above (Figure 4 ), which is why we left the temporal distributions only for Newman and Granovetter in Figure 6. The difference between the incoming regular and weighted degrees is relatively large, which means that many authors tend to cite other authors in many works. The fast growth from 2007 in most of the presented diagrams can be observed, which can be due to the significant attention that networks and network analysis received. Another explanation could be the inclusion of additional journals in WoS.
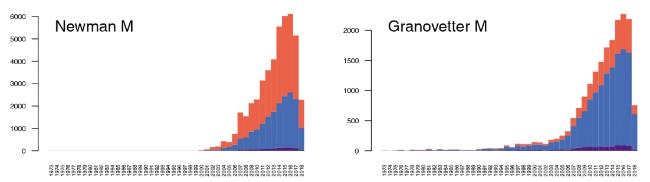
Figure 6. TACiA: Authors referencing authors: temporal indegree (blue/dark) and weighted indegree (red/light), TACiA′′: weighted indegree (purple/black). Note different y-scales. |
In Table 2 (2nd column), the authors with the average self-citation of 3 and more (loops from the network ACiA) are presented, varying from 2.98 (Latkin) to 6.47 (Dunbar). The number of works written by these authors is provided (1st column). Having information on the number of citations made by author a as weighted outdegACiA(a) (3rd column), it is possible to compute the percentage of self-citations among all citations of author a to all authors (5th column). Knowing the fractional contributions of all citations for each author as weighted outdegACiA″(a) (6th column), it is possible to compute the percentage of fractional self-citation among all citations of author a to all authors (8th column). For some authors, these values were relatively high. Values of 15% or more are marked in bold. Burt, Dunbar, Turel, Barabási, Newman, Christakis have the largest proportions of fractional self-citations. The metric of self-citation reflects research in a specialty area or conveys a pattern of a “cohesive and sustained research program” (Szomszor et al., 2020). A high value of self-citation can be interpreted as authors developing their own ideas and having their own specialty areas.
Table 2. Authors’ self-citation (ranked by average self-citation). Columns: # of works; average self-citation; # of all citations; # of self-citations; proportion (%) of self to all citations; fractional all citations; fractional self-citations; proportion (%) of fractional self to all citations. |
| Citation values, ACiA | Citation fractional values, AciA″ | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| N | Author | # Works | Av. self-cite | All | Self | Self / all, % | All | Self | Self / all, % |
| 1 | DUNBAR_R | 91 | 6.47 | 3,602 | 589 | 16.4 | 39 | 9.8 | 25.2 |
| 2 | FARINE_D | 34 | 5.62 | 2,447 | 191 | 7.8 | 13.5 | 1.8 | 13.5 |
| 3 | SHELDON_B | 19 | 4.95 | 1,455 | 94 | 6.5 | 4.9 | 0.4 | 7.4 |
| 4 | CROFT_D | 46 | 4.43 | 3,367 | 204 | 6.1 | 10.1 | 0.7 | 7.3 |
| 5 | ZENOU_Y | 35 | 4.17 | 1,074 | 146 | 13.6 | 17 | 2.3 | 13.3 |
| 6 | KRAUSE_J | 34 | 4.15 | 1,950 | 141 | 7.2 | 6.5 | 0.4 | 6.8 |
| 7 | KILDUFF_M | 30 | 4.1 | 1,711 | 123 | 7.2 | 12 | 1 | 8.6 |
| 8 | FARMER_T | 29 | 3.97 | 870 | 115 | 13.2 | 7.1 | 0.9 | 12.5 |
| 9 | CHRISTAK_N | 74 | 3.95 | 2,851 | 292 | 10.2 | 20.9 | 3.4 | 16.1 |
| 10 | BULL_C | 17 | 3.94 | 1,057 | 67 | 6.3 | 4.8 | 0.5 | 9.4 |
| 11 | HILARI_K | 10 | 3.9 | 371 | 39 | 10.5 | 3.6 | 0.4 | 11.8 |
| 12 | PATTISON_P | 58 | 3.86 | 2,411 | 224 | 9.3 | 18.4 | 1.6 | 8.5 |
| 13 | THURNER_S | 15 | 3.8 | 857 | 57 | 6.7 | 5.6 | 0.6 | 10.1 |
| 14 | BLUMSTEI_D | 15 | 3.8 | 899 | 57 | 6.3 | 5.6 | 0.6 | 10.3 |
| 15 | BURT_R | 71 | 3.77 | 1,681 | 268 | 15.9 | 50.2 | 17.3 | 34.4 |
| 16 | JAMES_R | 38 | 3.74 | 1,877 | 142 | 7.6 | 8.9 | 0.8 | 8.8 |
| 17 | STEGLICH_C | 30 | 3.73 | 1,482 | 112 | 7.6 | 8.4 | 0.5 | 5.8 |
| 18 | TUREL_O | 18 | 3.72 | 417 | 67 | 16.1 | 9.5 | 2.2 | 23 |
| 19 | FRANK_K | 28 | 3.68 | 974 | 103 | 10.6 | 10 | 1.2 | 11.9 |
| 20 | NORTHCOT_S | 9 | 3.67 | 343 | 33 | 9.6 | 3.2 | 0.4 | 10.9 |
| 21 | BRASS_D | 27 | 3.63 | 1,314 | 98 | 7.5 | 11.2 | 0.9 | 8.3 |
| 22 | ROBINS_G | 64 | 3.63 | 3,291 | 232 | 7 | 19.1 | 1.2 | 6.2 |
| 23 | CAIRNS_B | 15 | 3.53 | 359 | 53 | 14.8 | 3.9 | 0.5 | 12 |
| 24 | MEYBODI_M | 28 | 3.43 | 1,229 | 96 | 7.8 | 12.1 | 1.4 | 11.3 |
| 25 | FOWLER_J | 65 | 3.4 | 2,435 | 221 | 9.1 | 17.4 | 1.9 | 10.8 |
| 26 | SUEUR_C | 38 | 3.39 | 2,238 | 129 | 5.8 | 8.7 | 0.6 | 6.6 |
| 27 | DHIR_A | 15 | 3.33 | 969 | 50 | 5.2 | 5.1 | 0.2 | 4 |
| 28 | ROTHENBE_R | 32 | 3.31 | 1,169 | 106 | 9.1 | 10.2 | 1 | 9.5 |
| 29 | CHICLANA_F | 14 | 3.21 | 276 | 45 | 16.3 | 4 | 0.6 | 13.9 |
| 30 | NOWAK_M | 26 | 3.08 | 785 | 80 | 10.2 | 8.1 | 1.1 | 14.1 |
| 31 | NEWMAN_M | 81 | 3.06 | 2,392 | 248 | 10.4 | 48.7 | 9.3 | 19 |
| 32 | REZVANIA_A | 17 | 3.06 | 781 | 52 | 6.7 | 6.7 | 0.5 | 7.7 |
| 33 | POTTERAT_J | 20 | 3.05 | 644 | 61 | 9.5 | 4.4 | 0.4 | 8.2 |
| 34 | BARABÁSI_A | 67 | 3 | 1,769 | 201 | 11.4 | 19.3 | 3.9 | 20.3 |
| 35 | RICE_E | 48 | 2.98 | 2,040 | 143 | 7 | 13.1 | 1.4 | 10.9 |
| 36 | LATKIN_C | 130 | 2.98 | 4,467 | 387 | 8.7 | 31.6 | 3 | 9.4 |
For the same eight selected top authors from Table 1 , we traced the temporal distributions of self-citations (loops) in networks TACiA and TACiA″ (Figure 7 ). Among these top eight authors, only Newman, Barabási, and Burt appeared in Table 2 , having higher values of average self-citations, which are also seen from a temporal perspective. The values of self-citations vary from year to year when the authors use their previous works as a basis for their current research.
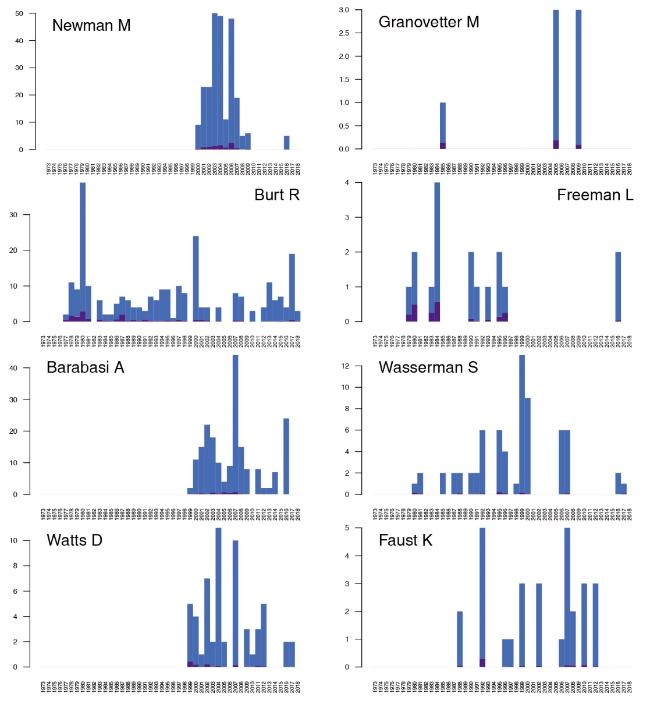
Figure 7. Self-citations in TACiA (blue/grey) and TACiA″ (purple/black). Note different y-scales. |
4.3 Meso-level: Groups of authors
In this subsection, we move to the meso-level of analysis and present the groups of authors in SNA that can be obtained from the derived networks of citations and bibliographic coupling between authors.
The network ACiA provides information on the number of citations between authors. Making a link cut at a threshold of 50 citations from the first author to the second author, we obtained the structure of the authors having the largest numbers of citations between each other. The obtained network (Figure 8 ) consists of 197 nodes and is composed of several components. The largest group of 106 nodes largely includes representatives of the network science discipline. It is centered (mostly) around Newman and (to a lesser degree) Barabási, who are also linked, as Newman cites other physicists Barabási, Albert, and Watts, and they cite each other (Barabási to Albert, Barabási to Watts). There are many authors with Chinese and Korean names attached to these authors; however, this might be an artifact of the author disambiguation problem: multi-personalities. Another group connected to a central node (Newman) consists of the representatives of machine learning and data mining areas from Japan, citing each other: Motoda, Saito, Kimura, and Ohara. Interestingly, there are two groups of authors from the areas that may look quite distant from the field of physics. One is represented by Dunbar and the authors around him, representing the field of social and evolutionary neuroscience, who became attached to this group through the works of Kaski from computational social science and statistical physics. Another group is represented by authors from animal social network analysis, which was shown as an important subfield in a recent study of the SNA field (Maltseva & Batagelj, 2019). It is connected to the central node (Newman) through Croft and has strong interconnections with James, J. Krause, and other representatives of behavioral ecology and sociobiology.
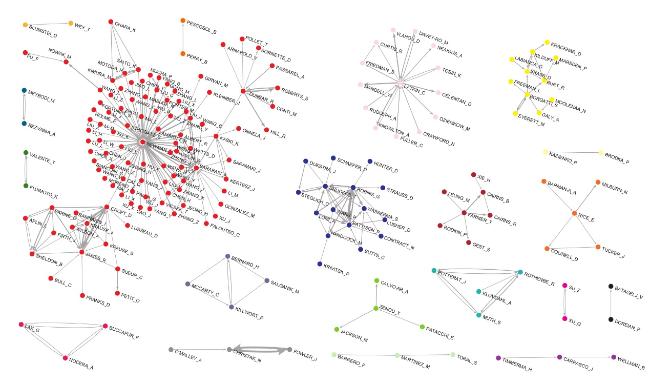
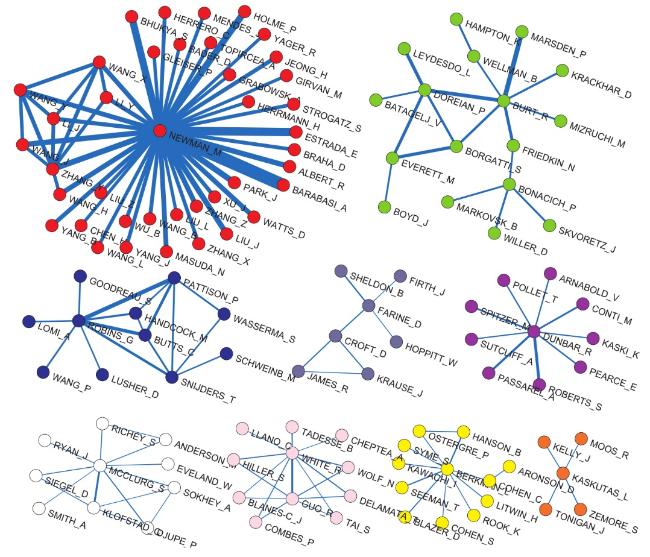
Figure 8. ACiA: Citations between authors. Link cut at level 50. Subnetworks with largest arc weights. |
Other groups are significantly smaller than the first group. The groups of 16, 14, and 11 nodes are formed by representatives of the social sciences. The star-like group formed around Latkin, representing health, behavior, and society studies, is not so interesting in the sense of structure, as it is composed of the authors citing and being cited by the central node. Two other groups are formed by the traditional representatives of SNA. The group of 16 nodes is formed by very well-known authors, Wasserman, Robins, Pattison, Snijders et al., who developed statistical models for social networks, such as exponential random graph (p*) models and stochastic actor-based models for network dynamics. Another group is also formed by well-known names in SNA, such as Borgatti, Everett, Freeman, Burt, Brass, Kilduff, Krackhardt, and Marsden. There are several smaller well-known groups of authors working on different SNA-related issues: network data collection (Bernard, Killworth, McCarty, Salganik), blockmodeling (Doreian, Batagelj), methodology (Valente, Fujimoto), internet networks (Wellman et al.), epidemiological and health studies (Christakis, Fowler, Malley).
Using the threshold of 140 citations from the network ACiA, we extracted the most related pairs of authors. These are the following pairs, with the number of citations given in brackets: Robins to Pattison (298), Fowler to Christakis (240), Christakis to Fowler (237), Croft to James (215), Croft to Krause (189), Newman to Barabási (147), Pattison to Robins (146), and Dunbar to Roberts (145). Using the network TACiA, we traced the temporal distributions of the citations between these pairs (Figure 9 ). The high number of citations is received through time, showing the appreciation of works for the selected authors.
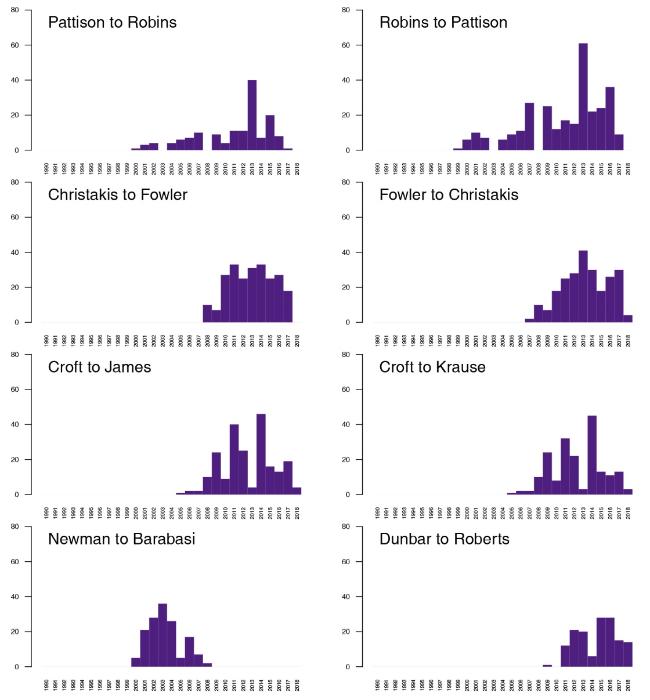
Figure 9. TACiA: Temporal distribution of citations for selected pairs of authors (First cites Second). |
To overcome the over-representation of authors with many works and works with many references, we used the normalized network ACiA′′ constructed using the fractional approach. To identify the groups of connected authors, we used the Islands approach, which was shown to be particularly useful for extraction of the most coherent “well connected” parts of networks (Batagelj et al., 2014, p.395-399). An island is a maximal connected subnetwork of vertices connected directly or indirectly by links with a value greater than that of the links to vertices outside the subnetwork. The approach allows us to consider the parts of the network of size at least k but not exceeding K, where k < K. Islands also enable us to identify locally important groups at different levels. We extracted islands of the size in the interval [10,200] from this network, which resulted in 37 islands (769 nodes, or 0.8% of all the nodes in network). The largest island of the ACiA′′ network consists of 200 nodes (26% of all nodes), and the additional 24% of nodes belong to clusters of sizes varying from 22 to 43 nodes. Half of the nodes in the obtained subnetwork belong to the islands consisting of 10-19 nodes. We tried to move the upper bound of the threshold to 500 nodes, and it resulted in the main island of 500 nodes, which means that there is a nested group of nodes. We can see that there are a large number of groups formed according to citations between the authors.
The main island of 200 nodes is presented in Figure 10. As the nodes form chains of citations from one author to the second, and then to the third, in the figure, blue represents the initial, only citing, node; yellow represents the intermediate, cited and citing, node; and pink represents the terminal, cited only, node. We can observe several different groups of authors in this subnetwork, interconnected to each other. The largest part of the subnetwork is represented by physicists centered around Newman (mostly), Barabási and Watts (to a lesser degree). Again, there are many authors with Chinese and Korean names in this part of the subnetwork, appearing only in a citing role. Brandes, a representative of the social/computer science part of network analysis, appears in this part of the subnetwork, being largely cited by J. Yang. The right part of the island is formed by several groups of authors from the social sciences. Some of them are centered around Granovetter, Freeman, and Burt, having many incoming citations; smaller groups are formed around Wellman and Scott. Other groups arise around the well-known authors who cite and are cited: Doreian, Leydesdorff, and Wasserman (with the group similar to the one observed in the results of ACiA network analysis above). This part of the island also includes other well-known researchers in SNA: White, Marsden, Everett, Borgatti, Carley, Breiger, et al. Between the two parts, we can observe intermediate nodes that cite the authors from the social sciences and network science groups. Their position implies only the usage of the two fields, but not the transfer of knowledge between them.
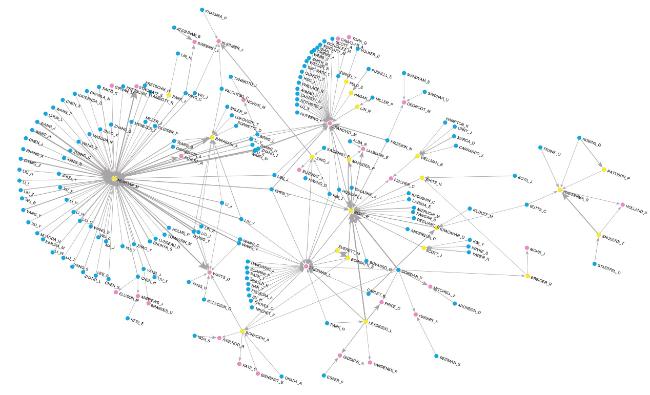
Figure 10. ACiA′′: Fractional citation between authors. Main island. |
Moreover, these are the authors Chinese and Korean names. However, we can notice the special position of Watts, who is cited by Bonacich (SNA) and Newman (NS) and can be classified as an author connecting two fields: physicist and sociologist.
Among the other 36 islands of sizes 10-43 nodes, many are not very interesting in terms of structure: they are star-like or (almost) complete clusters. To describe the majority of authors, a search for additional information is needed. Without having the time and space to drill into all the obtained islands, we decided to discuss only those with well-known names. Figure 11 shows several such islands with interesting structures, representing the authors from SNA or SNA-related areas. One of the islands includes one of the founding mothers of SNA, Bott, working on issues of family and social networks, starting from the 1950s. Another island is centered on Rogers, with Valente as one of the citing authors, developing the topic of the diffusion of innovations. Another island is partly centered on Rheingold (virtual communities), and in another part includes the authors from political science working on social media analysis. Other groups include Latkin and Radloff, Berkman and Litwin, and Christakis and Fowler - the authors working in epidemiological and health studies. Among the islands with star-like structures, we identified well-known authors with many incoming citations. Interestingly, some belong to the field of SNA, such as Dunbar (social and evolutionary neuroscience) and Portes (social capital). Other largely cited authors are quite distant from the field of SNA, though they provide an important conceptual and theoretical basis for the field: Wenger (communities of practice) and Prensky (digital natives and immigrants), Castells (theory of information and network society), Latour (actor-network theory, ANT), and Goffman (sociological theorizing of social interaction).
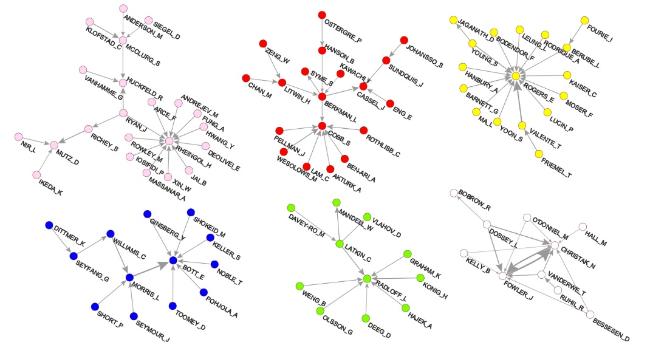
Figure 11. ACiA′′: Fractional citation between authors. Selected islands. |
Bibliographic coupling shows the similarity of the authors according to the overlap of their references (same topics of interests) and does not require the authors to be aware of each other’s citing practices. Again, we used the Islands approach and extracted 9 islands, which contain from 5 to 40 nodes (Figure 12 ).
Figure 12. Jaccard network ACoj: General islands. |
In Figure 12 , the largest island on the left comes from the physics literature and is centered on Newman. Most of the authors in this island have Chinese and Korean names, but it also includes well-known physicists mentioned in the previous analysis of citation networks: Barabási, Albert, Watts, and Strogatz. The second and third islands are formed by the groups of classical social network scientists.
While 17 authors (with Burt, Doreian, Everett, and Borgatti having the largest indegree weights, i.e. the citation similarity with others) included in the second island work on more general issues of SNA, 11 authors (Robins, Pattison, Snijders, Butts, Wasserman et al.) forming the third island work on statistical models for social networks. The separation of this subgroup from the other SNA authors was also identified by the citation analysis. Bonachich, having a bridging position between the groups of SNA and network science representatives above, is connected to the SNA group according to his citing patterns. The fourth island shows the similarity in citation patterns between the authors from the field of animal SNA: James, J. Krause, Croft, Farine et al. There are five more islands of star-like structures, centered around Dunbar, mentioned above, McClurg (political participation), White (economics), Berkman (social epidemiology), and Kaskutas (alcohol treatment).
The analysis of the citation and bibliographic coupling networks clearly shows the existence of two main branches in the field under study: the first is formed by the many well-known names in SNA, and the second consists of authors from the network science discipline. The second branch is larger according to the number of its representatives in all the obtained substructures. However, many of them are authors of Chinese and Korean names, which is not reliable in terms of the author disambiguation problem. The topics of interest (represented by the cited works/authors) of the SNA representatives vary, which leads to the separation of some subgroups into smaller ones. The most visible subgroup is formed by the SNA authors developing statistical models for social networks; smaller groups of authors working on different SNA-related aspects are also identified. The analysis reveals that some authors take a bridging position, for example, Watts. Besides these two large branches, the analysis also extracts other groups representing different fields of study, being close or far from the field. The group of authors representing animal SNA, revealed through the analysis of the ACiA and ACoj networks, is connected to the network science branch, but not to the social science one. The results are discussed below.
5 Conclusions
In this study, we used citation network analysis to study the structure of the scientific community currently involved in SNA. As many classical works in bibliometrics and scientometrics have shown, the analysis of direct citations between authors can identify the main scholars in the field and core research groups, whereas bibliographic coupling analysis can reveal groups of authors studying similar subjects. Overall, the analysis of the cognitive and social contexts of a knowledge claim can bring important results to the understanding of the current development of a scientific discipline (Leydesdorff, 1998), identifying its scientific schools, invisible colleges (Price, 1963), or author citation clubs (Brandes & Pich, 2011).
In the case of SNA, the establishment of a community with shared knowledge has already been shown by early studies (Freeman, 2004; Hummon & Carley, 1993). However, the later contributions from various disciplines outside social sciences made SNA more complex in the sense of the groups of scholars involved. Many previous studies on SNA development showed that the most obvious distinction was between the two groups of scholars: those from social sciences representing the “classical” SNA and those representatives of natural sciences and computer science, who entered the field in the 2000s and led to the development of the network science discipline. However, many of the studies were conducted almost a decade ago, with different data collection strategies, which included different disciplines in the scope of the analysis. Little attention has been given to the analysis of the citation and bibliographic coupling structures of the SNA representatives. This highlights the relevance of the current study, where we used a comprehensive approach to data collection up to 2018. In the previous studies, we have already analyzed the structures of citations between works, and journals, keywords co-occurrence networks, and collaboration structures of authors publishing papers in the field of SNA (Maltseva & Batagelj, 2019, 2020, 2021, 2022).
Observing the general citation patterns in the field on the macro-level, we found that more than half of the authors under consideration of the study have no received citations from any works in our dataset. Half of those who received at least one citation were cited in one, two, or three works from our dataset. Overall, 80% of the authors did not have more than 15 citations received from other works. It is possible that the authors have more citations, but not by the authors in the field of SNA, who were included in our dataset. We can propose that the network follows the power law like distribution, as it was shown in the research of Silva et al. (2020). We also observed patterns of self-citation in the field. For the majority of authors, the value of the average self-citation is either equal to 0 or is very low.
However, at the micro-level of analysis, we observed a small group of authors whose values of the received citations are extremely high. We used different network measures to extract the top 50 authors, and the list of top 10 authors is formed by the same well-known scholars: Newman (on the first place) followed by Granovetter, Wasserman, Faust, Burt, Freeman, Borgatti, Barabási, Albert, and Watts. Among the three sets of top 50 authors, 32 authors appear in all three lists, which means that different measures are quite close in identifying the most prominent scholars. Most of the authors identified as prominent by Brandes and Pich (2011) can also be found in these lists. The temporal distributions provided for a selected group of top authors show that the time periods of citations accumulation can vary. In our data, selected sociologists collected their incoming citations over their whole professional lives starting from the 1970s, while selected physicists obtained the maximum values of citations only from the 2000s. For most of the selected authors, fast growth from 2007 can be observed, which can be due to the significant attention that networks and network analysis have received or the inclusion of some relevant journals in WoS. On the temporal diagrams, we also noted the large differences between the incoming regular and weighted degrees, which means that many authors are referenced several times in a work. Such citation patterns can be the basis for the creation of author groups, or “clubs” (Brandes & Pich, 2011).
For a small group of authors, the values of average self-citation are relatively high. However, among these authors, the proportions of authors’ self-citations to their total citations in reference lists vary significantly. In previous studies, the average indicators of self-citation were not more than 10% (Kacem et al., 2020; Szomszor et al., 2020) or 12.7% (Ioannidis et al., 2019) (though it was emphasized that the values can vary a lot across scientific disciplines). We selected a threshold of 15% of self-citation, and the largest values correspond to Burt, Dunbar, Turel, Barabási, Newman, and Christakis. Although there has been a long discussion about the self-mentioning practices in bibliometric and scientometric literature (Helper et al., 2015; Ioannidis et al., 2019; Kacem et al., 2020; MacRoberts & MacRoberts, 1989; Szomszor et al., 2020), we stand at the point that self-citation mostly means that the scholars build their current research on topics focused on their own previous studies and developments.
The analysis of citation and bibliographic coupling networks at the meso-level supported the existence of two main groups in the SNA field, as shown by Brandes and Pich (2011) and Batagelj et al. (2020). One branch is formed by the many well-known names in SNA, and the second consists of authors from the network science discipline. The second branch is larger according to the number of its representatives in all the substructures. However, many of them are authors of Chinese and Korean names, which can be multi-personalities (Harzing, 2015). In fact, this branch is based on several well-known physicists, such as Newman, Barabási, Albert, Watts, and Strogatz. In contrast, the social branch contains more authors, who are also very well known. In different subgroups, the names of Borgatti, Breiger, Burt, Carley, Doreian, Everett, Freeman, Granovetter, Krackhardt, Leydesdorf, Marsden, White, et al. appear, citing each other and studying similar topics. As the direct citation and reference patterns of the SNA representatives vary, this branch has a more complex structure, which implies the separation of some subgroups. The most visible subgroup was formed by SNA authors who developed statistical models for social networks: Wasserman, Robins, Pattison, Snijders, et al. Smaller groups of authors working on different SNA-related aspects were also identified, such as network data collection (Bernard, Killworth, McCarty, Salganik), methodology (Valente, Fujimoto), including, for example, blockmodeling (Doreian, Batagelj), internet networks (Wellman), epidemiological and health studies using network models (Latkin, Litwin, Christakis, Fowler, Malley), and social and evolutionary neuroscience (Dunbar). The group of authors working on health-related issues was one of the two identified by Brandes and Pich (2011). Some of the identified subgroups were formed around the authors, who provided an important conceptual basis for the field, such as Bott (family and social networks), Rogers (diffusion of innovations), or Portes (social capital). Coming back to the division of the field into two large parts, the analysis reveals that some authors take a bridging position, for example, the sociologist and physicist Watts in the analysis of normalized citation network, who is cited by Bonachich and Newman. Such connecting cases can be very important for the field’s shared identity.
In addition to these two large branches, the analysis also extracted other groups representing different fields of study. The existence of a number of groups of authors shows that SNA attracts attention from many groups of scholars. We were not able to drill into all the obtained groups, and we focused only on those authors who are well-known in the field of SNA. We found the names of the more general scholars, providing a conceptual basis to the studies, such as Rheingold (virtual communities), Wenger (communities of practice), Prensky (digital natives), or giving a theoretical background, such as Castells (theory of information and network society), Latour (actor-network theory, ANT), and Goffman (sociological theorizing of social interaction). They appear in the table of the most cited authors as well. The group that did not appear in the previous analyses is the one formed by the authors representing animal SNA. Through their citation practices, the authors from this group are connected to the network science branch, but not the social science branch. A previous analysis (Maltseva & Batagelj, 2019) also showed the connections of literature in animal SNA to the network science literature.
Thus, we were able not only to identify the general division of the authors into the two obvious groups of social scientists and physicists, which has been shown in many other studies, but also to show that the first group itself has a more complex structure and that there are a number of other groups of authors from different disciplines in the field. With its growth and development, SNA attracts more and more scholars, and the question arises: Should we talk about the community or communities of SNA practitioners? We believe that with all the institutional support formed through the years, the authors in SNA can be seen as a community, which, however, has its local “colleges” and “clubs”, unified by a shared literature and knowledge base. The examples of the brokerage between different groups are very important to maintain the common identity of the field and merge the separate branches of studies into the whole multidisciplinary field.
In this paper, we identified and applied an innovative approach and methods to study the structure of scientific communities, which allowed us to get the findings going beyond those obtained with other methods. We used a new approach to temporal network analysis (Batagelj & Maltseva, 2020; Batagelj & Praprotnik, 2016). We consider this approach an important addition to the analysis, as it provides detailed information on different measures for the authors and pairs of authors over time. The next step of this approach could be the temporal visualization of the authors’ groups. The methodological contribution of this study is that the provided approach can be utilized for similar objectives, identifying key structures and characteristics in other disciplines.
As a limitation of the study, we faced the author disambiguation, or “multiple personalities” (Harzing, 2015) problem. The main challenge in this approach is the resolution of the author’s name (synonyms and homonyms). This problem would be simplified by the standardization of information stored in bibliographic databases (ORCID, DOI, ISSN, ISBN, etc.). To be consistent with our other studies, we had to stick to working to the dataset collected up to 2018. The analysis of the updated networks based on Scopus (Baas et al., 2020) (see Appendix A) or OpenAlex (2024) can provide new insights about the field’s development and can be performed in the future.
Another issue that we would like to discuss as a limitation concerns the dataset of the study. Even though we tried to make the dataset as inclusive and robust as possible, it is still limited by the boundaries that we created: the papers we included in the analysis were written on the topic of social networks, intensively referenced by these publications, written by the most prominent authors, or published in the top journals in SNA. This should have made the authors working in the field of SNA mainly be highly represented in the dataset. However, the authors dealing with other issues except for network analysis could not have been fully represented in the dataset by the volume of their scientific production. For such peripheral authors, the structures shown here could not be correct because most of their works lie outside of the dataset, and we do not have information on them. We would like to stress that the analysis and conclusions on the activity, productivity, and visibility of the authors are relative only to the field of SNA; the authors that appeared here could have different results relative to other fields of activity. However, such problem of “lack of full context” perspective is typical to other scientometric analyses based on keyword searches, which results should be considered with care to prevent misassignment and misinterpretation of the non-central authors. We expect that iterated saturation data collection approach we used attracted most of the important works noticed by the network analysis community.
We expect that the results of our current research will be of interest to both the SNA community and a broader group of researchers. Network researchers can find some useful information in the series of publications on this project (Maltseva & Batagelj, 2019, 2020, 2021, 2022), which could be important for understanding the current status of the SNA field’s development. Besides the historiographical value, the “who-is-who” information is important for the internal reflection of the SNA practitioners and could stimulate some efforts for the knowledge exchange between different branches of the community. The joint work of community members could lead to the formation of network analysis as a solid discipline and methodology widely used in various fields of science. For a wider group of researchers, the current study could become an example of systematic analysis, which could be applied to their own fields and disciplines. This may potentially inspire the application of bibliometric network analysis and other network approaches in various research areas, creating more authors collaborating in the field of SNA.
Acknowledgments
All computations were performed using the program for large network analysis and visualization Pajek (De Nooy et al., 2018) and Python code based on library Nets (Batagelj, 2020b). Visualizations of distributions and temporal quantities were produced in R. We appreciate the help of the Academic Writing Center, Higher School of Economics, Moscow with the proofreading of the article.
Funding information
This work is supported in part by the Slovenian Research Agency (VB, research program P1-0294), (VB, research project J5-2557), (VB, research project J5-4596); COST EU (VB, COST action CA21163 (HiTEc)); and is prepared within the framework of the HSE University Basic Research Program.
Author contributions
Daria Maltseva (dmaltseva@hse.ru, ORCID: 0000-0003-1789-1711): Data curation (Equal), Formal analysis (Equal), Visualization (Supporting), Writing - original draft (Lead).
Vladimir Batagelj (vladimir.batagelj@fmf.uni-lj.si, ORCID: 0000-0002-0240-9446): Conceptualization (Lead), Data curation (Equal), Formal analysis (Equal), Investigation (Lead), Methodology (Lead), Software (Lead), Supervision (Lead), Visualization (Lead), Writing - review & editing (Supporting).
Data availability statement
The data that support the findings of this study are available from the corresponding author, Daria Maltseva, upon reasonable request.
Appendix
A: The impact of multi-person units on derived bibliographic networks
One of the crucial problems in the transformation of bibliographic data into corresponding networks is the identification of bibliographic units (authors, works, journals, countries, keywords, etc.). Some bibliographic databases provide besides unit names their unique identifiers (DBLP, MathSciNet, Scopus, OpenAlex) DBLP (2024); TePaske-King and Richert (2001); Baas et al. (2020) making the transformation much easier. In general, this is not the case (Harzing, 2015). We would like to study the effect of multi-persons, and in general multi-units, in derived networks.
Let M = [m[u,v]] be a matrix on U × V and CU = {C1,C2,...,Ck} a partition of the set U, ∅ ⊂ Ci ⊆ U, Ci ∩ Cj = ∅ for i ≠ j, and ∪i Ci = U. The set U is the (ground truth) set of real units (persons). The partition CU corresponds to units (for example, authors) identified by the network construction process. A cluster C ∈ CU with |C| > 1 represents a multi-unit; and for |C| = 1 a correctly identified unit.
We introduce the shrinking transformation Sr of matrix M by the rows partition CU into Sr(M,CU) = S = [s[C,v]] on CU × V determined by the rule
$s[C, v]=\sum_{u \in C} m[u, v]$
The shrinking transformation can be extended to a columns partition CV of the set V by
$s[u, C]=\sum_{v \in C} m[u, v]$
or
$S_{c}\left(\mathbf{M}, \mathbf{C}_{V}\right)=S_{r}\left(\mathbf{M}^{T}, \mathbf{C}_{V}\right)^{T}$
and to partitions CU and CV of both sets by
$S\left(\mathbf{M},\left(\mathbf{C}_{U}, \mathbf{C}_{V}\right)\right)=S_{c}\left(S_{r}\left(\mathbf{M}, \mathbf{C}_{U}\right), \mathbf{C}_{V}\right)$
Consider now the case of two compatible matrices M = [m[u, t]] on U × T and N = [n[t, v]] on T × V. For a partition CU of the set U it holds
$S_{r}\left(\mathbf{M} \cdot \mathbf{N}, \mathbf{C}_{U}\right)=S_{r}\left(\mathbf{M}, \mathbf{C}_{U}\right) \cdot \mathbf{N}$
To check this let’s denote with L and R the left and right sides of this expression. We have
$l[C, v]=\sum_{u \in C} \mathbf{M} \cdot \mathbf{N}[u, v]=\sum_{u \in C} \sum_{t \in t} m[u, t] \cdot n[t, v]$
and
$r[C, v]=\sum_{t \in T} S_{r}\left(\mathbf{M}, \mathbf{C}_{U}\right)[C, t] \cdot n[t, v]=\sum_{t \in T}\left(\sum_{u \in C} m[u, t]\right) \cdot n[t, v]=l[C, v]$
For the partition CV of the set V we get
$\begin{array}{l} S_{c}\left(\mathbf{M} \cdot \mathbf{N}, \mathbf{C}_{V}\right)=S_{r}\left((\mathbf{M} \cdot \mathbf{N})^{T}, \mathbf{C}_{V}\right)^{T}=S_{r}\left(\mathbf{N}^{T} \cdot \mathbf{M}^{T}, \mathbf{C}_{V}\right)^{T}= \\ =\left(S_{r}\left(\mathbf{N}^{T}, \mathbf{C}_{V}\right) \cdot \mathbf{M}^{T}\right)^{T}=\mathbf{M} \cdot S_{r}\left(\mathbf{N}^{T}, \mathbf{C}_{V}\right)^{T}=\mathbf{M} \cdot S_{c}\left(\mathbf{N}, \mathbf{C}_{V}\right) \end{array}$
Therefore
$S_{c}\left(\mathbf{M} \cdot \mathbf{N}, \mathbf{C}_{V}\right)=\mathbf{M} \cdot S_{c}\left(\mathbf{N}, \mathbf{C}_{V}\right)$
For partitions of both sets U and V we have
$\begin{array}{c} S\left(\mathbf{M} \cdot \mathbf{N},\left(\mathbf{C}_{U}, \mathbf{C}_{V}\right)\right)=S_{c}\left(S_{r}\left(\mathbf{M} \cdot \mathbf{N}, \mathbf{C}_{U}\right), \mathbf{C}_{V}\right)= \\ =S_{c}\left(S_{r}\left(\mathbf{M}, \mathbf{C}_{U}\right) \cdot \mathbf{N}, \mathbf{C}_{V}\right)=S_{r}\left(\mathbf{M}, \mathbf{C}_{U}\right) \cdot S_{c}\left(\mathbf{N}, \mathbf{C}_{V}\right) \end{array}$
and finally
$S\left(\mathbf{M} \cdot \mathbf{N},\left(\mathbf{C}_{U}, \mathbf{C}_{V}\right)\right)=S_{r}\left(\mathbf{M}, \mathbf{C}_{U}\right) \cdot S_{c}\left(\mathbf{N}, \mathbf{C}_{V}\right)$
For Cu ∈ CU and Cv ∈ CV we have
$\begin{array}{c} S\left(\mathbf{M} \cdot \mathbf{N},\left(\mathbf{C}_{U}, \mathbf{C}_{V}\right)\right)\left[C_{u}, C_{v}\right]=S_{c}\left(S_{r}\left(\mathbf{M} \cdot \mathbf{N}, \mathbf{C}_{U}\right), \mathbf{C}_{V}\right)\left[C_{u}, C_{v}\right]= \\ \sum_{z \in C_{v}} S_{r}\left(\mathbf{M} \cdot \mathbf{N}, \mathbf{C}_{U}\right)\left[C_{u}, z\right]=\sum_{z \in C_{v}} \sum_{w \in C_{u}} \mathbf{M} \cdot \mathbf{N}[w, z]=\sum_{w \in C_{u}} \sum_{z \in C_{v}} \mathbf{M} \cdot \mathbf{N}[w, z] \end{array}$
In a special case of singelton clusters Cu = {u} and Cv = {v} we get
$S\left(\mathbf{M} \cdot \mathbf{N},\left(\mathbf{C}_{U}, \mathbf{C}_{V}\right)\right)\left[C_{u}, C_{v}\right]=\sum_{w \in\{u\}} \sum_{z \in\{v\}} \mathbf{M} \cdot \mathbf{N}[w, z]=\mathbf{M} \cdot \mathbf{N}[u, v]$
We see that the multi-units don’t affect the values of relations between singletons in the derived networks.
B: Totals
In this section we provide proofs of properties of totals of some derived networks listed in Subsection 3.4. In the proofs we will use the relations
$\sum_{a \in A} \mathbf{W A}[w, a]=\text { outdeg }_{\mathbf{W A}}(w)$
$\sum_{t \in W} \mathbf{C i t e}[w, t]=\text { outdeg }_{\mathbf{C i t e}}(w)$
$n(\mathbf{W A})[w, a]=\frac{\mathbf{W A}[w, a]}{\max \left(1, \text { outdeg }_{\mathbf{W A}}(w)\right)}$
$n(\mathbf{C i t e})[w, t]=\frac{\text { Cite }[w, t]}{\max \left(1, \text { outdeg }_{\mathbf{C i t e}}(w)\right)}$
$W_{\mathbf{W A}}^{+}=\left\{w \in W: \text { outdeg }_{\mathbf{W A}}(w)>0\right\}$
$T(\mathbf{N})=\sum_{(u, v) \in L} w(u, v)$
$δ(true) = 1 and δ(false) = 0$
B.1 CiA′
This derived network is defined as CiA′ = Cite ∗ n(WA). For its total T(CiA′) we get
$\begin{array}{c} T\left(\mathbf{C i A}^{\prime}\right)=\sum_{w \in W} \sum_{a \in A} \sum_{t \in W} \operatorname{Cite}[w, t] \cdot n(\mathbf{W A})[t, a]= \\ \sum_{w \in W} \sum_{t \in W} \operatorname{Cite}[w, t] \cdot \frac{\sum_{a \in A} \mathbf{W A}[t, a]}{\max \left(1, \operatorname{outdeg}_{\mathbf{W A}}(t)\right)}= \\ \sum_{w \in W} \sum_{t \in W} \operatorname{Cite}[w, t] \cdot \delta\left(\operatorname{outdeg}_{\mathbf{W A}}(t)>0\right)=\sum_{w \in W} \sum_{t \in W_{\mathbf{W A}}^{+}} \operatorname{Cite}[w, t]= \\ \sum_{t \in W_{\mathrm{WA}}^{+}} \operatorname{indeg}_{\mathbf{C i t e}}(t) \leq \sum_{t \in W} \operatorname{indeg}_{\mathbf{C i t e}}(t)=\left|L_{\mathbf{C i t e}}\right| \end{array}$
B.2 CiA″
This derived network is defined as CiA″ = n(Cite) ∗ n(WA). For its total T(CiA″) we get
$\begin{array}{l} T\left(\mathbf{C i A}^{\prime \prime}\right)=\sum_{w \in W} \sum_{a \in A} \sum_{t \in W} n(\mathbf{C i t e})[w, t] \cdot n(\mathbf{W A})[t, a]= \\ \sum_{w \in W} \sum_{a \in A} \sum_{t \in W} \frac{\text { Cite }[w, t]}{\max \left(1, \text { outdeg }_{\text {Cite }}(w)\right)} \cdot \frac{\text { WA }[t, a]}{\max \left(1, \text { outdeg }_{\mathbf{W A}}(t)\right)}= \\ \sum_{w \in W} \sum_{t \in W} \frac{\text { Cite }[w, t] \cdot \delta\left(\text { outdeg }_{\mathbf{W A}}(t)>0\right)}{\max \left(1, \text { outdeg }_{\text {Cite }}(w)\right)} \leq \\ \sum_{w \in W} \sum_{t \in W} \frac{\text { Cite }[w, t]}{\max \left(1, \text { outdeg }_{\text {Cite }}(w)\right)}=\sum_{w \in W} \frac{\text { outdeg }_{\text {Cite }}(w)}{\max \left(1, \text { outdeg }_{\text {Cite }}(w)\right)}= \\ \sum_{w \in W} \delta\left(\text { outdeg }_{\text {Cite }}(w)>0\right)=\left|W_{\text {Cite }}^{+}\right| \leq|W| \end{array}$
B.3 ACiA′
This derived network is defined as ACiA′ = n(WA)T ∗ Cite ∗ n(WA). For its total T(ACiA′) we get
$\begin{array}{c} T\left(\mathbf{A C i A} \mathbf{C i}^{\prime}\right)=\sum_{a \in A} \sum_{b \in A} \sum_{w \in W} \sum_{t \in W} n(\mathbf{W A})^{T}[a, w] \cdot \mathbf{C i t e}[w, t] \cdot n(\mathbf{W A})[t, b]= \\ \sum_{a \in A} \sum_{b \in A} \sum_{w \in W} \sum_{t \in W} \frac{\mathbf{W A}[w, a]}{\max \left(1, \text { outdeg }_{\mathbf{W A}}(w)\right)} \cdot \mathbf{C i t e}[w, t] \cdot \frac{\mathbf{W A}[t, b]}{\max \left(1, \boldsymbol{o u t d e g}_{\mathbf{W A}}(t)\right)}= \\ \sum_{w \in W} \sum_{t \in W} \delta\left(\text { outdeg }_{\mathbf{W A}}(w)>0\right) \cdot \mathbf{C i t e}[w, t] \cdot \delta\left(\boldsymbol{o u t d e g}_{\mathbf{W A}}(t)>0\right) \leq \\ \sum_{w \in W} \sum_{t \in W} \mathbf{C i t e}[w, t]=\sum_{t \in W} \operatorname{indeg}_{\text {Cite }}(t)=\left|L_{\mathbf{C i t e}}\right| \end{array}$
B.4 ACiA″
This derived network is defined as ACiA″ = n(WA)T ∗ n(Cite) ∗ n(WA). For its total T(ACiA″) we get
$\begin{array}{c} T\left(\mathbf{A C i A}^{\prime \prime}\right)=\sum_{a \in A} \sum_{b \in A} \sum_{w \in W} \sum_{t \in W} n(\mathbf{W A})^{T}[a, w] \cdot n(\mathbf{C i t e})[w, t] \cdot n(\mathbf{W A})[t, b]= \\ \sum_{a \in A} \sum_{b \in A} \sum_{w \in W} \sum_{t \in W} \frac{\mathbf{W A}[w, a]}{\max \left(1, \text { outdeg }_{\mathbf{W A}}(w)\right)} \cdot n(\mathbf{C i t e})[w, t] \cdot \frac{\mathbf{W A}[t, b]}{\max \left(1, \text { outdeg }_{\mathbf{W A}}(t)\right)}= \\ \sum_{w \in W} \sum_{t \in W} \delta\left(\text { outdeg }_{\mathbf{W A}}(w)>0\right) \cdot n(\mathbf{C i t e})[w, t] \cdot \delta\left(\text { outdeg }_{\mathbf{W A}}(t)>0\right) \leq \\ \sum_{w \in W} \sum_{t \in W} n(\mathbf{C i t e})[w, t]=\sum_{w \in W} \sum_{t \in W} \frac{\text { Cite }[w, t]}{\max \left(1, \text { outdeg }_{\text {Cite }}(w)\right)}= \\ \sum_{w \in W} \frac{\operatorname{outdeg}_{\text {Cite }}(w)}{\max \left(1, \operatorname{outdeg}_{\text {Cite }}(w)\right)}=\sum_{w \in W} \delta\left(\operatorname{outdeg}_{\text {Cite }}(w)>0\right)=\left|W_{\text {Cite }}^{+}\right| \leq|W| \end{array}$
It is easy to check that in the above inequalities the equality holds if each work has at least one author and has a nonempty (reduced) list of references.