1 Introduction
Research evaluation based on publications and citations is one of the most important applications of bibliometrics (Garfield & Welljams-Dorof, 1992). Without research evaluations that describe the research systems of countries, research policies are arbitrary. However, research has multiple impacts on society, and assessments based on publications and citations measure the impact that drives the progress of scientific knowledge, but probably not other types of impacts (Aksnes et al., 2019; Aksnes et al., 2023). These other types of societal impacts are also crucially important; however, their assessment requires different approaches (Bornmann, 2013; Bozeman & Sarewitz, 2011).
Regarding contributions to the progress of knowledge, research systems can be assessed in terms of either size or efficiency. For size, the method may be as simple as counting the number of publications; however, for efficiency, the assessment is a much more difficult task. At a low level of aggregation, research assessments based on publication outputs should be performed by peer review; however, at the country or even institution level (Martin, 2011), these dimensions make it very difficult to organize peer review assessments. In these cases, bibliometric assessments seem to be the best solution (Abramo et al., 2013; Abramo et al., 2019).
Bibliometric evaluations have been performed for a long time (Godin, 2006; Leydesdorff, 2005), boosted by the pioneering study of Francis Narin (1976). Regretfully, in too many cases, research success has been defined “operationally” as simply amounting to the score of the proposed index (Harnad, 2009). With significant progress in the current century (Aksnes et al., 2019; Tahamtan & Bornmann, 2019; Waltman, 2016), many studies have demonstrated that citation-based metrics are the most convenient indicators for research evaluation (Aksnes et al., 2019; Waltman, 2016) if they are used at a high aggregation level (Aksnes et al., 2023; Thelwall et al., 2023).
A great number of citation-based parametric and nonparametric indicators have been proposed over the last 20-30 years (Van Noorden, 2010; Wildgaard et al., 2014). Among them, the top percentile indicators (Bornmann et al., 2013; Waltman & Schreiber, 2013) are preferred by the most well-known international or national institutions. Some examples are the OECD, the U.S. National Science Board, the European Commission, National Institute of Science and Technology Policy in Tokyo, and CWTS of the University of Leiden. These indicators are accurate and reliable if the results at different percentiles fit a power law (Rodríguez-Navarro & Brito, 2019). In the other cases, they failed. Japan is a good example of these failures because it is a country with a high scientific level that the top percentile and other indicators suggest is a research-developing country (Pendlebury, 2020).
The power law that percentiles and other rank-based indicators follow represents an ideal model. Similar to how real gases frequently deviate from the ideal gas law, the research outputs of some institutions and countries deviate from the ideal model. These deviations give rise to uncertain rankings of countries and institutions, because Japan does not need to be an isolated case of misjudgment (Rodríguez-Navarro, 2024b).
In addition to these deviations, or perhaps as the basis of these deviations, research may be addressed to produce either incremental innovations or scientific advancements with different citation practices (Rodríguez-Navarro & Brito, 2022). Consequently, studies that focus on understanding the bibliometric differences between these two types of research are at the forefront of scientometric research.
1.1 Wrong diagnoses and misguided research policies
The notion that a suitable research policy must be based on reliable research assessments is both rational and empirical. A well-known example of a wrong diagnosis of research success that misguides research policy is the EU. This failure was described 18 years ago (Dosi et al., 2006), and subsequent publications have demonstrated its permanence. First, the EU’s research policy was dominated by the “European paradox” (Albarrán et al., 2010), and later, when many academic publications criticized the paradox, the same idea was expressed by the catchphrase: “Europe is a global scientific powerhouse” (Rodríguez-Navarro & Brito, 2020b). In contrast with this political propaganda of success, the analysis of the most cited papers shows that, in terms of contribution to pushing the boundaries of knowledge, the EU is well behind the USA and China in most technological fields (Rodríguez-Navarro, 2024a).
The case of the EU is only one example; the same problem likely affects many other countries. The comparison between Norway and Singapore is another example. These two countries have a similar number of inhabitants, and in both countries, the GDP per capita is very high, implying that research is not restricted by economic difficulties. Despite these similarities, an analysis of the global ranks of the most cited papers in technological topics shows Singapore’s overwhelming superiority (Rodríguez-Navarro, 2024a). This implies that the research success suggested by some bibliometric analyses (Sivertsen, 2018) does not exist and that, in comparison to Singapore, Norwegian research policy is far from successful.
An incorrect diagnosis can occur in both senses, overstating or understating the real success. In contrast to the overestimations described above, Japan is trying to boost the global ranking of its universities (Normile, 2024), but its research level is probably much better (Rodríguez-Navarro, 2024a) than that suggested by common indicators (Pendlebury, 2020), even when they are obtained in Japan (National Institute of Science and Technology Policy, 2022).
In summary, accurate research assessments are necessary for accurate research policies and successful contributions to scientific and technological progress.
1.2 Global ranks and deviations from the ideal power law
In the ideal model mentioned above, when global and local publications are ordered from the highest to lowest number of citations, local versus global ranks fit a power law (Rodríguez-Navarro & Brito, 2018). Plotting this relationship on a double-logarithmic scale produces a straight line in which deviations are easily detected. In ideal cases, there is an easily testable property because Ptop 10%/P, Ptop 5%/Ptop 50%, and Ptop 1%/Ptop 10% are equal (henceforth, I will use the Leiden Ranking notation; Ptop x% means the number of papers in the top x% by citation), and the number of papers in all top percentiles can be easily calculated from P and the number in a single top percentile (Rodríguez-Navarro & Brito, 2021). However, the publications of many research systems do not fit the ideal model (Rodríguez-Navarro, 2024b).
Country rankings published by the OECD (2016), the European Commission (2022), Japan (National Institute of Science and Technology Policy, 2022), France (Science and Technology Observatory, 2019), and other international and national institutions use the share of the top 10% of most-cited scientific publications as a measure of scientific excellence. This would seem to be a reasonable method because the top percentiles have been validated by correlation against the results of the UK Research Excellence Framework, which is based on peer review (Rodríguez-Navarro & Brito, 2020a; Traag & Waltman, 2019). However, it would be difficult to find a senior researcher who believes that one in 10 scientific publications makes a significant contribution to the advancement of science. Therefore, a high share of the top 10% of most-cited scientific publications could be taken as success in normal research, but not in revolutionary research (Kuhn, 1970). The revolutionary research that pushes the boundaries of knowledge must be evaluated in much narrower percentiles, in the range of the 0.01-0.02% most-cited papers (Bornmann et al., 2018; Poege et al., 2019). However, as mentioned above, if research outputs fit the ideal model, evaluations based on the top 10% most-cited papers could be used to evaluate breakthroughs that are 1,000 times less frequent (Rodríguez-Navarro & Brito, 2019), but only in these cases.
1.3 Scientometric challenges
Research has diverse impacts on society (Bornmann, 2013; Greenhalgh et al., 2016; Martin, 1996), leading to the conclusion that it cannot be assessed using a single indicator. In contrast, the effect of research on science can be described exclusively as its contribution to the progress of knowledge. In principle, with this restriction, a single research indicator may be sufficient to describe the efficiency of a research system. However, this is not entirely correct because research can be aimed at two different objectives: boosting incremental innovations or pushing the boundaries of knowledge. These two types of research have different citation practices, with citations being less frequent in technical research, and are mixed in different proportions in most countries and institutions. Furthermore, citation-based rank analyses (e.g. top percentile indicators) are based on the comparison of global and local citation distributions, and a reasonable conjecture is that the ideal rank power law appears when the proportions of these two types of research in the country or institution under evaluation are similar to the proportions in global research. Japan does not fulfill this requirement, and for this reason, its evaluations fail (Rodríguez-Navarro, 2024b). The same can also be observed in other countries and institutions.
To overcome these difficulties, the evaluation can focus on the contribution of pushing the boundaries of knowledge at citation levels that correspond only to this type of research. The evaluations can then be performed using a single indicator (Rodríguez-Navarro & Brito, 2024). However, even in this case, the challenge remains unresolved. An indicator based on the most cited papers is size-dependent and provides no information about the efficiency of the system, which implies that the comparison of countries or institutions of different sizes is impossible. In other words, the indicator does not convey to what extent successful achievements stem from size or efficiency.
In summary, it is not clear how to obtain comprehensive research evaluations that provide solid information to research policymakers. This drawback does not exist in those cases that conform to the ideal rank power law, but this does not occur universally.
1.4 Aim of this study
The uncertainty regarding the accuracy of research indicators directly calculated from easily measured statistical data, such as Ptop 10%/P or Ptop 1%/P, prompted a study of the relationships between citation distributions and the accuracy of these indicators. For this purpose, this study assumes two ideal models, a lognormal distribution for citations and a power law relationship between global and local ranks of papers, and investigates the deviations from these ideal models. Deviations in the upper tail are important regarding their contribution to pushing the boundaries of knowledge, but they have been studied (Rodríguez-Navarro, 2024b; Rodríguez-Navarro & Brito, 2024). Currently, the most important challenge is in the lower tail and part of the citation distribution of papers that are not highly cited.
This study uses research topics, which imply more homogeneous populations of papers than fields, which aggregate many topics. It has two parts: the first investigates the deviations from the ideal model at global and country levels, while the second focuses on journals to study more homogeneous and diverse populations of papers than in the cases of countries or institutions. It was conjectured that journal publications should facilitate the analysis of indicators and study of extreme cases. It is unlikely that the publications of a country or institution have a global success equivalent to that of journals such as Nature or Science. However, a comprehensive description should also consider these extreme cases.
2 Methods
This study is based on citation data obtained from the Clarivate Web of Science, as described in a previous paper (Rodríguez-Navarro, 2024b), using the same publication (2014-2017) and citation (2019-2022) windows, as well as domestic publications. The recorded journal impact factors (JIF) correspond to 2019. In the searches, the topic referred to in the text as “solar cells” also includes “photovoltaics,” and the case referred to as “dementia” also includes “Parkinson” and “Alzheimer.”
To construct the rank plots, either for countries or journals, global papers were ordered by the number of citations from highest to lowest, with one assigned to the most cited paper. Because many papers have the same number of citations, to construct more accurate rankings, in addition to the number of citations, the papers were subsequently ordered by publication year, average number of citations per year, and DOI. To obtain the global ranks of country papers, these papers were ordered as global papers, and the papers in this list were identified in the global list together with their global ranks. To find the global ranks of journal papers, the global list was ordered alphabetically by journal name and segmented for each journal.
The logarithmic bins of citation distributions are shown in the histograms, which also include the number of papers with zero, one, and two citations. Normal probability plots of the log-transformed number of citations (or citations plus 1, if on the list there are papers with zero citations) were constructed, as described by Boylan and Cho (2012). The plotting positions were obtained using the formula pi = (i-٠.٥)/n, where n is the number of papers. The results of the Kolmogorov-Smirnov goodness-of-fit tests of the log-transformed numbers of citations were obtained at https://contchart.com/goodness-of-fit.aspx.
The proportion of lowly cited and uncited papers in the citation distribution of countries and journals is of special interest in this study. These papers may belong to a specific type that is abundant in highly technological countries (Rodríguez-Navarro & Brito, 2022), but this relationship has not been specifically investigated. The proportion of uncited papers is probably the best indicator for the entire population of papers of this type, and in this sense, as an indicator of a population of papers, is used throughout this study.
3 Results
3.1 Deviations from the rank power law: countries
The proportion of uncited papers varies notably among research topics (Rodríguez-Navarro, 2024b). In the 10 technical and biomedical topics studied here, the proportion of uncited papers varied from 11% for semiconductors to 3% for lithium batteries and dementia (Table 1 ). Despite this variability, the normal probability plots of the log-transformed number of citations (plus 1) reveal very similar inflated lower tails compared to the rest of the papers. Figure 1 depicts the plots for lithium batteries and semiconductors.
Table 1. Number of papers and proportion of uncited papers in the selected research topics. |
| Topic | Number | MNCa | Uncited (%) |
|---|---|---|---|
| Semiconductors | 58,393 | 18.4 | 10.8 |
| Steel | 69,128 | 13.8 | 8.9 |
| Concrete | 34,126 | 17.1 | 7.9 |
| Solar cells | 61,202 | 22.3 | 7.6 |
| Combustion | 38,403 | 16.7 | 5.9 |
| Immunity | 42,586 | 21.8 | 4.4 |
| Stem cells | 86,647 | 20.9 | 4.3 |
| Graphene | 82,757 | 29.9 | 3.8 |
| Dementia | 39,767 | 22.6 | 3.2 |
| Lithium batteries | 32,318 | 32.4 | 3.1 |
a Mean number of citations. |
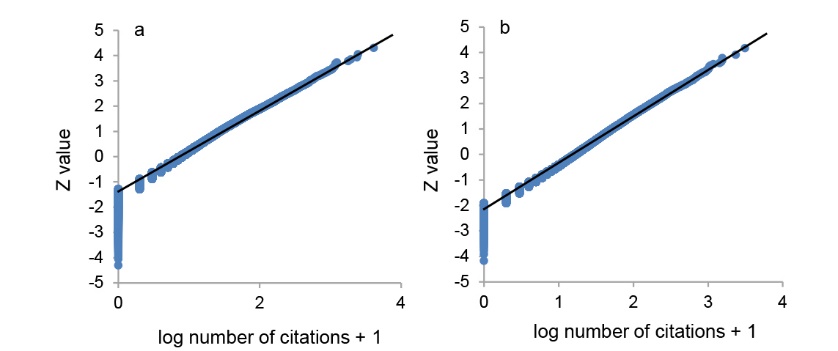
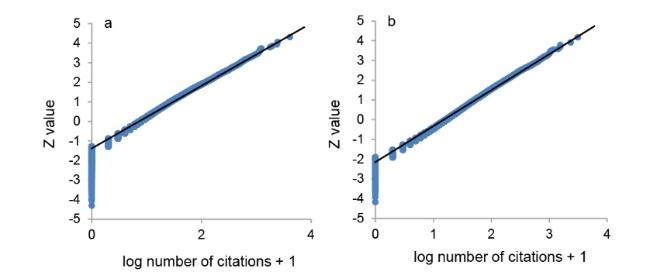
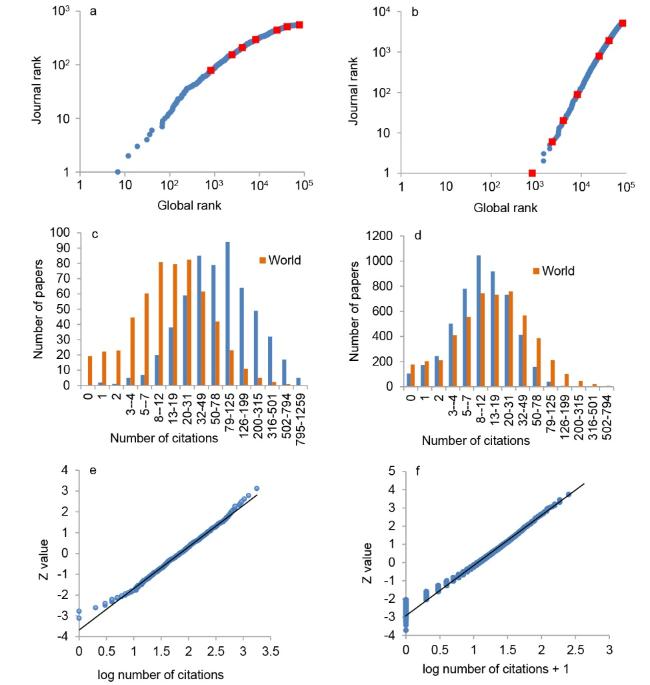
Figure 1. Normal probability plots of the log-transformed number of citations plus 1 of publications in the topics of semiconductors (a) and lithium batteries (b). |
Confirming a previous study (Rodríguez-Navarro, 2024b), it is found that a notable number of countries deviate from the ideal model (Ptop 10%/P = Ptop 5%/Ptop 50% = Ptop ٣٪/Ptop ٣٠٪ = Ptop 1%/Ptop 10%), which indicates that research country rankings based on a single indicator, either Ptop 10%/P or Ptop 1%/P, can be misleading, depending on the selected countries. Tables 2 and 3 show the results for the 16 countries in the research topics of graphene and solar cells. Deviations of Ptop 1%/Ptop 10% exclusively indicate a deviation in the extreme of the upper tail that might affect a very low proportion of papers (Rodríguez-Navarro, 2024b). Excluding this ratio, it can be concluded that roughly, the number of countries that significantly deviate from the ideal model is around 50% or even more.
Table 2. Basic description of publications on graphene from selected countries, including percentile ratios. |
| Country | Pa | P0b(%) | MNCc | Ptop 10%/P | Ptop 5%/Ptop 50% | Ptop 3%/Ptop 30% | Ptop 1%/Ptop 10% |
|---|---|---|---|---|---|---|---|
| China | 35,493 | 3.6 | 31.8 | 0.104 | 0.102 | 0.098 | 0.088 |
| EU | 7,555 | 7.1 | 22.3 | 0.059 | 0.080 | 0.088 | 0.107 |
| USA | 5,784 | 5.1 | 42.1 | 0.127 | 0.166 | 0.194 | 0.221 |
| South Korea | 4,701 | 5.2 | 24.1 | 0.078 | 0.069 | 0.065 | 0.054 |
| India | 3,794 | 3.1 | 21.1 | 0.049 | 0.034 | 0.023 | |
| Japan | 1,788 | 10.3 | 17.0 | 0.041 | 0.094 | 0.108 | 0.095 |
| Germany | 843 | 4.2 | 21.4 | 0.064 | 0.097 | 0.102 | |
| Singapore | 683 | 2.3 | 47.8 | 0.182 | 0.175 | 0.163 | 0.121 |
| UK | 666 | 2.7 | 27.1 | 0.083 | 0.078 | 0.095 | |
| Italy | 664 | 3.6 | 18.1 | 0.039 | 0.039 | ||
| Spain | 657 | 2.3 | 22.4 | 0.055 | 0.055 | 0.053 | |
| Australia | 552 | 2.0 | 47.9 | 0.199 | 0.209 | 0.213 | 0.155 |
| Canada | 514 | 3.7 | 29.5 | 0.097 | 0.088 | 0.092 | |
| France | 410 | 5.9 | 21.4 | 0.066 | 0.067 | ||
| Switzerland | 136 | 6.6 | 26.4 | 0.088 | 0.127 | ||
| Netherlands | 132 | 2.3 | 34.0 | 0.136 | 0.131 |
a Number of publications. b Uncited papers. c Mean number of citations. |
Table 3. Basic description of publications on solar cells from selected countries, including percentile ratios. |
| Country | Pa | P0b(%) | MNCc | Ptop 10%/P | Ptop 5%/Ptop 50% | Ptop 3%/Ptop 30% | Ptop 1%/Ptop 10% |
|---|---|---|---|---|---|---|---|
| China | 12,806 | 7.7 | 18.8 | 0.086 | 0.085 | 0.083 | 0.064 |
| EU | 8,170 | 5.8 | 18.4 | 0.082 | 0.066 | 0.056 | 0.048 |
| USA | 5,471 | 4.6 | 32.6 | 0.146 | 0.141 | 0.139 | 0.141 |
| South Korea | 4,188 | 13.9 | 17.8 | 0.066 | 0.077 | 0.087 | 0.104 |
| India | 3,118 | 5.8 | 14.1 | 0.051 | 0.040 | 0.035 | |
| Japan | 2,727 | 12.3 | 13.8 | 0.059 | 0.079 | 0.095 | 0.093 |
| Germany | 1,829 | 6.4 | 17.4 | 0.078 | 0.080 | 0.076 | 0.063 |
| Italy | 1,161 | 4.0 | 20.5 | 0.091 | 0.053 | 0.034 | |
| UK | 890 | 4.3 | 43.1 | 0.179 | 0.176 | 0.204 | 0.208 |
| Australia | 803 | 4.7 | 24.0 | 0.130 | 0.102 | 0.081 | |
| Spain | 794 | 5.3 | 19.1 | 0.081 | 0.060 | 0.051 | |
| France | 673 | 5.9 | 15.0 | 0.062 | 0.044 | 0.048 | |
| Canada | 546 | 6.0 | 24.8 | 0.106 | 0.084 | 0.083 | |
| Singapore | 363 | 4.7 | 27.1 | 0.132 | 0.129 | 0.140 | 0.167 |
| Switzerland | 345 | 3.5 | 49.3 | 0.209 | 0.251 | 0.248 | 0.167 |
| Netherlands | 304 | 3.3 | 21.1 | 0.099 | 0.083 | 0.063 |
a Number of publications. b Uncited papers. c Mean number of citations. |
When deviations from the ideal model are small, the double rank plots show that the countries’ comparisons are accurate. For example, this is the case in the comparisons of Spain and Singapore in graphene, and the USA and Germany in solar cells (Figure 2 ). In these cases, differences in size should not be an impediment to finding an accurate indicator of efficiency that, along with the difference in size, clearly defines the research differences between the two countries. In contrast, when the deviations from the ideal system are large, finding indicators that reveal the differences in size and efficiency of the two countries seems very difficult. This is the case in the comparison of Japan and India in graphene (Table 2 ; Figure 3 ). Depending on the publications considered, the comparative judgment of research efficiency (from the slope of the fitted straight lines) changes depending on the rank range considered. Considering the 50% least cited papers, India seems to be more efficient than Japan, but using the 10% most cited papers, the conclusion is the opposite. More importantly, if we calculate the efficiency from the 10% most cited papers, we will assess the size of the research system in India as larger than it is, while in Japan, the assessment would be smaller than it is.
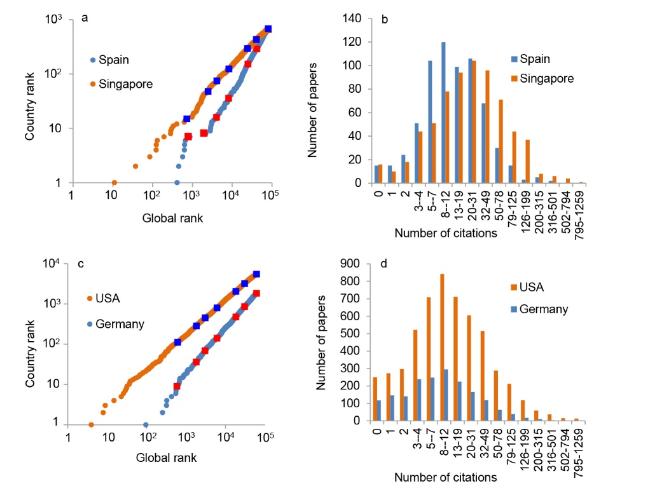
Figure 2. Double rank plots (a, c) and citation distributions (b, d) of publications from Spain and Singapore in graphene (a, b) and the USA and Germany in solar cells (c, d). Square symbols in (a) and (c) represent the position of papers in the top percentiles: 1, 3, 5, 10, 30, 50, and 100, from bottom to top. |
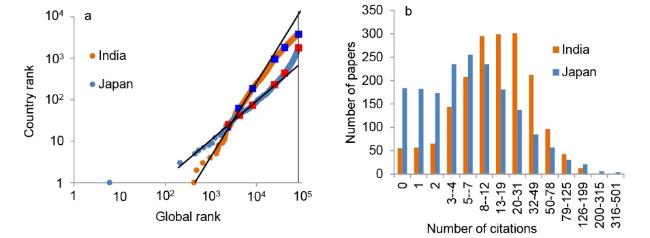
Figure 3. Double rank plots (a) and citation distribution (b) of publications from India and Japan on graphene. Square symbols in (a) represent the position of papers in the top percentiles: 3, 5, 10, 30, 50, and 100, from bottom to top. In (b), the number of papers from India (3,794) was scaled down to the number of papers from Japan (1,788). |
Despite the described differences, in the two research topics and 16 countries depicted in Tables 2 and 3 , the well-known strong relationship between Ptop 10%/P and the mean number of citations (MNC) (Perianes-Rodriguez & Ruiz-Castillo, 2016; Waltman et al., 2012) holds (Pearson correlation coefficients of 0.97 in graphene and 0.98 in solar cells, P < 0.0001 in both cases).
3.2 Basic description of journals
To further investigate the complexity of citation distributions and their effect on research assessments, I studied journal publications in a selection of 10 research topics (Table 1 ), paying special attention to the proportion of uncited papers. As a general rule, although the number of journals that publish papers on a certain topic is very high, the number of journals that publish many papers is much lower. For example, in the field of graphene, over the four years of this study, I retrieved 82,757 papers published in 1,648 journals; however, only 250 journals published more than 50 papers, 135 journals published more than 100 papers, and 31 journals published more than 500 papers. Notably, 406 journals published only one paper.
In contrast to countries where the absence of uncited papers is infrequent or perhaps never occurs (Tables 2 and 3 ), many journals on the research topics studied here do not publish papers that are not cited, or they occur at a very low proportion (Table 4 ). Many of these journals have high JIFs, such as the Journal of the American Chemical Society or ACS Nano in technological fields or Science or Cell in biomedical fields (JIFs in the range of 15-25). However, there are also journals with lower impact factors that either have no uncited papers or a very low proportion of them. Scientific Reports (JIF, 4.0) is an example of such journals. Interestingly, in many of these journals, goodness-of-fit tests support a lognormal citation distribution (Table 4 shows the results of the Kolmogorov-Smirnov test of the log-transformed data). As expected (Perianes-Rodriguez, 2016; Waltman, 2012), the mean number of citations (MNC) in the publication and citation windows of this study (four years in both cases) was highly correlated with the JIF (Pearson coefficient 0.84; P < 0.0001).
Overall, in terms of technological topics, I found that many journals with a significant proportion of uncited papers have the word “applied” in their names or are published by well-known technological institutions. For example, in the first case, the Journal of Applied Physics and Applied Physics Letters, and in the second case, several journals published by the Institute of Electrical and Electronics Engineers (IEEE). Journals with a high proportion of uncited papers were less frequent in biomedicine, even in journals dealing with technical applications. For example, in the topic of stem cells, the number of uncited papers in the journal Cytotherapy was only 3%.
I also found a group of journals on all topics whose main characteristics are that their most cited papers have a low number of citations and that the proportion of uncited papers is high. These journals may be highly specialized or published in countries that are developing their research systems. In other cases, they are open-access journals that might belong to the category of predatory journals.
Table 4. Basic description of journal publications in four research topics, including goodness-of-fit to lognormal distribution. |
| Topic | Journal | JIFa | Pb | P0c(%) | MNCd | KSf P-value |
|---|---|---|---|---|---|---|
| Semiconductors | Journal of the American Chemical Society | 14.7 | 437 | 0 | 85.8 | > 0.15 |
| Semiconductors | Advanced Materials | 25.8 | 396 | 0 | 78.7 | > 0.15 |
| Semiconductors | Angewandte Chemie-International Edition | 13.0 | 262 | 0.4 | 77.0 | > 0.15 |
| Semiconductors | ACS Nano | 14.6 | 584 | 0.3 | 59.7 | > 0.15 |
| Semiconductors | ACS Applied Materials & Interfaces | 8.5 | 1,120 | 1.1 | 28.6 | 0.01 |
| Semiconductors | Scientific Reports | 4.0 | 1,101 | 1.1 | 20.1 | < 0.01 |
| Solar Cells | Journal of the American Chemical Society | 14.7 | 486 | 0 | 121.0 | 0.05 |
| Solar Cells | Advanced Materials | 25.8 | 653 | 0 | 103.9 | < 0.01 |
| Solar Cells | Nano Letters | 12.3 | 460 | 0.2 | 73.5 | > 0.15 |
| Solar Cells | Advanced Energy Materials | 24.9 | 665 | 0 | 52.4 | > 0.15 |
| Solar Cells | Applied Energy | 8.4 | 453 | 0.2 | 40.4 | < 0.01 |
| Solar Cells | Scientific Reports | 4.0 | 805 | 0.6 | 26.9 | < 0.01 |
| Stem cells | Science | 41.1 | 112 | 0 | 190.8 | > 0.15 |
| Stem cells | Nature | 43.1 | 279 | 0 | 180.5 | 0.01 |
| Stem Cells | Cell | 36.2 | 167 | 0 | 168.3 | > 0.15 |
| Stem cells | Nature Communications | 11.9 | 691 | 0 | 51.6 | > 0.15 |
| Stem cells | Blood | 16.6 | 673 | 0.1 | 46.9 | 0.08 |
| Stem cells | Development | 5.8 | 483 | 0.4 | 29.0 | 0.02 |
| Lithium batteries | Advanced Materials | 25.8 | 274 | 0 | 149.1 | > 0.15 |
| Lithium batteries | Journal of the American Chemical Society | 14.7 | 159 | 0 | 139.8 | > 0.15 |
| Lithium batteries | Advanced Energy Materials | 24.9 | 434 | 0 | 93.9 | < 0.01 |
| Lithium batteries | Nano Letters | 12.3 | 313 | 0 | 91.5 | > 0.15 |
| Lithium batteries | Nano Energy | 15.6 | 479 | 0 | 63.5 | < 0.01 |
| Lithium batteries | Scientific Reports | 4.0 | 410 | 0 | 33.7 | 0.14 |
a Journal Impact Factor. b Number of publications. c Number of uncited papers. d Mean number of citations. f Kolmogorov-Smirnov test of log-transformed number of citations. |
Although the reasons for the different proportions of uncited papers were beyond the scope of this study, a noticeable characteristic in the journals studied is that the proportions of uncited papers in a certain journal on different topics reflect the different proportions of global uncited papers on these topics. Table 5 shows the proportion of uncited papers in the same 20 journals on lithium batteries and solar cells: 3.1% and 7.6% of uncited papers, respectively. The two percentages of uncited papers in the two topics across journals were highly correlated (Pearson coefficient 0.92; P < 0.0001), and the ratio between these percentages was almost identical to that existing in the global papers on the two topics.
Table 5. Proportion of uncited papers in the same journals of publications in the research topics of lithium batteries and solar cells. |
| Journal | Lithium batteries | Solar cells | ||
|---|---|---|---|---|
| Pa | P0b(%) | P | P0 (%) | |
| Advanced Materials | 274 | 0.00 | 653 | 0.00 |
| Journal of the American Chemical Society | 159 | 0.00 | 486 | 0.00 |
| Advanced Energy Materials | 432 | 0.00 | 665 | 0.00 |
| Nano Letters | 313 | 0.00 | 458 | 0.22 |
| Applied Energy | 193 | 0.00 | 453 | 0.22 |
| Nano Energy | 479 | 0.00 | 440 | 0.45 |
| Scientific Reports | 410 | 0.00 | 805 | 0.62 |
| Journal of Materials Chemistry A | 2,095 | 0.14 | 1,681 | 0.71 |
| ACS Applied Materials & Interfaces | 1,416 | 0.14 | 1,799 | 1.11 |
| Chemistry of Materials | 529 | 0.19 | 549 | 0.36 |
| Journal of Physical Chemistry C | 624 | 0.48 | 1,549 | 2.52 |
| Journal of Power Sources | 2,813 | 0.50 | 501 | 1.80 |
| Chemical Communications | 352 | 0.57 | 434 | 0.92 |
| Physical Chemistry Chemical Physics | 514 | 0.58 | 927 | 1.73 |
| Electrochimica Acta | 2,382 | 0.67 | 689 | 3.48 |
| Journal of Alloys and Compounds | 839 | 1.07 | 644 | 3.11 |
| RSC Advances | 1,634 | 2.14 | 1,941 | 3.66 |
| Journal of the Electrochemical Society | 1,339 | 2.39 | 206 | 8.74 |
| Journal of Materials Science: Materials in Electronics | 122 | 3.28 | 705 | 11.21 |
| Materials Letters | 411 | 3.41 | 424 | 6.60 |
a Number of papers. b Uncited papers. |
3.3 Deviations from the rank power law: journals
In all the cases studied, deviations of the global ranks of journal papers from a power law are frequent and show many similarities. Table 6 presents a basic analysis of 20 journals with JIFs ranging from 26 to 2 in the research topic of graphene. This table presents the top percentile ratios for testing the ideal rank power law (Ptop 10%/P = Ptop 5%/Ptop 50% = Ptop ٣٪/Ptop ٣٠٪ = Ptop 1%/Ptop 10%). This method can only be applied to journals where the numbers of papers in the top 5% or 3% of the most cited papers are statistically significant, which occurs only in journals with high JIFs or many publications. The first conclusion drawn from the data is that, as a general rule, journals with JIFs above approximately 4.0, notably deviate from the rank power law. Most of these journals do not have uncited papers, or their proportion is very low. Generally, the proportion of uncited papers increases as JIF decreases. Notably, the well-known relationship between Ptop 10%/P and MNC (Perianes-Rodriguez & Ruiz-Castillo, 2016; Waltman et al., 2012) applies to journals (Pearson correlation coefficient, 0.99, P < 0.0001).
Table 6. Basic description of journal publications and percentile ratios in the research topic of graphene. |
| Journal | JIFa | Pb | P0c (%) | MNCd | Ptop10%/ P | Ptop5%/Ptop50% | Ptop3%/Ptop30% | Ptop1%/Ptop10% |
|---|---|---|---|---|---|---|---|---|
| Advanced Materials | 25.8 | 809 | 0.25 | 129.3 | 0.604 | 0.462 | 0.361 | 0.249 |
| Nature Communications | 12.1 | 558 | 0.00 | 129.1 | 0.529 | 0.409 | 0.347 | 0.268 |
| Journal of the American Chemical Society | 14.7 | 285 | 0.00 | 122.2 | 0.519 | 0.386 | 0.330 | 0.277 |
| Advanced Functional Materials | 16.8 | 626 | 0.00 | 91.8 | 0.450 | 0.309 | 0.259 | 0.160 |
| ACS Nano | 14.6 | 1,115 | 0.09 | 82.6 | 0.383 | 0.284 | 0.249 | 0.164 |
| Nano Letters | 11.2 | 956 | 0.21 | 64.8 | 0.306 | 0.227 | 0.189 | 0.106 |
| ACS Applied Materials & Interfaces | 8.8 | 2,837 | 0.14 | 49.0 | 0.231 | 0.129 | 0.088 | 0.038 |
| ACS Sustainable Chemistry & Engineering | 7.6 | 346 | 0.29 | 47.8 | 0.223 | 0.124 | 0.066 | 0.013 |
| Journal of Materials Chemistry A | 11.3 | 2,646 | 0.11 | 43.5 | 0.190 | 0.087 | 0.053 | 0.026 |
| Nanoscale | 6.9 | 1,933 | 0.52 | 34.2 | 0.130 | 0.077 | 0.050 | |
| Journal of Power Sources | 8.2 | 1,024 | 0.39 | 33.6 | 0.113 | 0.038 | 0.032 | |
| Carbon | 8.8 | 2,339 | 1.20 | 30.9 | 0.111 | 0.081 | 0.066 | |
| Scientific Reports | 4.0 | 2,008 | 0.90 | 29.4 | 0.092 | 0.056 | 0.048 | |
| 2D Materials | 5.5 | 414 | 0.72 | 27.8 | 0.075 | 0.048 | ||
| Electrochimica Acta | 6.2 | 2,217 | 0.13 | 24.9 | 0.042 | 0.016 | 0.012 | |
| Journal of Physical Chemistry C | 4.2 | 1,310 | 1.83 | 22.2 | 0.059 | 0.039 | 0.030 | |
| Physical review B | 3.6 | 2,027 | 3.90 | 15.3 | 0.033 | 0.049 | 0.047 | |
| RSC Advances | 3.1 | 5,127 | 2.05 | 15.7 | 0.017 | 0.010 | ||
| Applied Physics Letters | 3.6 | 1,188 | 3.70 | 14.1 | 0.016 | 0.017 | ||
| Journal of Applied Physics | 2.3 | 682 | 6.01 | 9.4 | 0.007 |
a Journal Impact Factor. b Number of papers. c Uncited papers. d Mean number of citations. Ptop x%, Number of papers in top percentile x. |
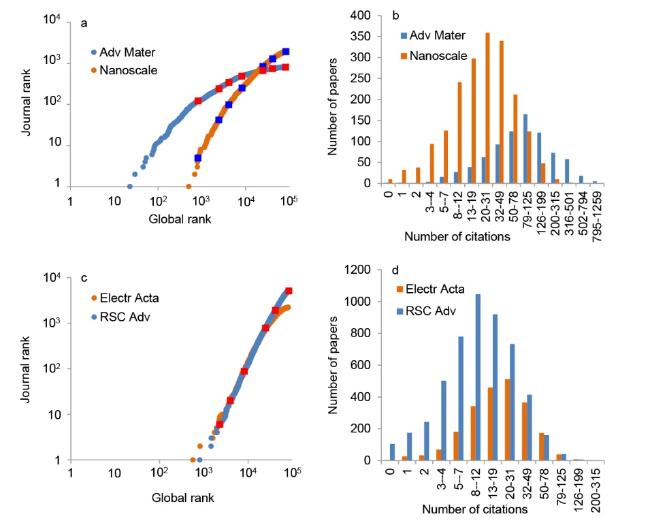
Figure 4. Publications on graphene in journals Nature Communications (a, c, e) and RSC Advances (b, d, f). Double rank plots (a, b), citation distributions (c, d), and normal probability plots (e, f). In (a) and (b), square symbols represent the position of papers in the top percentiles: 1, 3, 5, 10, 30, 50, and 100, from bottom to top. Histograms in (c) and (d) include world publications, which have been scaled down to the number of publications in the journals: from 82,757 to 5,127 and 558, respectively. |
The double rank plot of Nature Communications (Figure 4 ) represents the extreme of the deviations of journals’ plots from a straight line, deviations that disappear in journals with JIFs of approximately 4 or lower. This implies that in many journals, evaluations based on the number of papers and a single indicator do not describe the data. For example, Figure 5 shows a comparison of Advanced Materials with Nanoscale (JIFs, 25.8 and 6.9, respectively) and of Electrochimica Acta with RSC Advances (JIFs, 6.2 and 3.1, respectively). The first case (panels a and b) shows that Advanced Materials notably exceeds Nanoscale in the probability of publishing highly cited papers, but the obvious difference cannot be accurately described with a single parameter. The number of papers is higher in Nanoscale (1,933 versus 809), while Ptop 10% and Ptop 1% are higher in Advanced Materials (489 versus 251 and 122 versus 5). Furthermore, if we calculate the ratios between these parameters (Ptop 10%/P, Ptop 1%/P, and Ptop 1%/Ptop 10%), the differences between the two journals are so disproportioned (0.6 versus 0.12, 0.15 versus 0.003, 0.25 versus 0.02) that it would be illogical to select only one of them to describe the journals’ difference.
Figure 5. Publications on graphene in journals Advanced Matter, Nanoscale, Electrochimica Acta, and RSC Advances. Double rank plots (a, c) and citation distributions (b, d). In (a) and (c), square symbols represent the position of papers in the top percentiles: 1 3, 5, 10, 30, 50, and 100, from bottom to top. In panel c, Ptop 1% is not marked. |
In the second case (panels c and d), in terms of the number of publications, RSC Advances more than double Electrochimica Acta (5,127 versus 2,217, respectively), but the double rank plots of the top 30% cited papers are almost identical in both journals. Consequently, Ptop 10% has almost the same value in the two journals (785 and 743, respectively). If we define the efficiency in the rank range of the top 30% most cited papers, the two journals are equal, but the Ptop 10%/P ratio of Electrochimica Acta doubles that of RSC Advances (0.34 versus 0.15). The important difference in “efficiency” between the two journals is in the lowly cited papers. In highly cited papers, the two journals are identical. Again, it is doubtful that these differences can be described using a single indicator.
These results suggest that differences in the proportion of uncited papers between journals and global publications affect the double rank plots. However, graphene is a research topic with a low proportion of uncited papers, which raises the question of whether in a topic with a higher proportion of uncited papers (e.g. semiconductors), the conclusions would be different. To investigate this issue, I compared the double rank plots of the same two journals, ACS Applied Materials and Interfaces and Scientific Reports (JIFs, 8.8 and 4.0; uncited papers, 0.14% and 0.90%; Table 6 ), in the two research topics of graphene and semiconductors, which have different proportions of uncited papers (3.8% and 10.8%, respectively; Table 1 ). The results (Figure 6 ) show that the plot of Scientific Reports in semiconductors deviates more from linearity (increased curvature) than that in graphene, but this does not occur in ACS Applied Materials and Interfaces. These results suggest that the proportion of uncited papers in the topic contributes to deviations of the double rank plot from linearity, but that this contribution is negligible in journals with high JIF, which show high deviations even in topics with a low proportion of uncited papers.
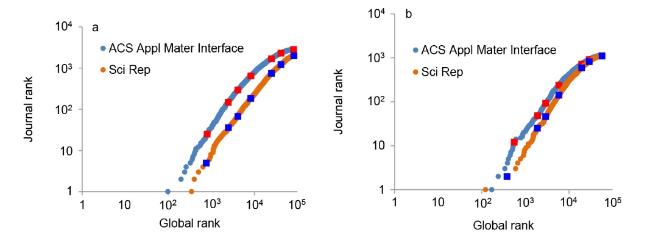
Figure 6. Double rank plots of publications in graphene (a) and semiconductors (b) in the journals ACS Applied Materials and Interfaces and Scientific Reports. Square symbols represent the position of papers in the top percentiles: 1, 3, 5, 10, 30, 50, and 100, from bottom to top. |
3.4 Log-log double rank plots can have positive and negative curvatures
The results depicted in Figure 3 reveal that the log-log double rank plot corresponding to the lower tail can have downward or upward concavity. Downward concavity can be easily studied in journals, but not upward concavity. The former appears when the journal has a lower proportion of uncited papers than global publications, and the latter should appear in journals with a higher proportion of uncited papers than global publications. These journals exist, but most of their publications are lowly cited. Consequently, all papers are grouped in the lower tail of the global citation distribution, and in these cases, the double rank plot does not deviate or deviates very little from a power law.
Therefore, I investigated this issue further in different countries. Table 7 depicts the Ptop 50%/P and Ptop 5%/Ptop 10% ratios in 11 countries (for statistical robustness, the number of countries is reduced with reference to Tables 2 and 3 ; in all cases, Ptop 5% > 22) in the topics of graphene and solar cells. The Ptop 50%/P ratio corresponds to the maximum curvature in the log-log double rank plots (Figures 5 and 6 ), and the Ptop 5%/Ptop 10% ratio corresponds to the top 10% tail, which fits the power law in countries (Figure 3 ). In countries with ideal systems, the Ptop 50%/P and Ptop 5%/Ptop 10% ratios are equal.
Table 7. Percentile ratios of publications from countries on the research topics of graphene and solar cells. |
| Country | Graphene | Solar cells | ||
|---|---|---|---|---|
| Ptop 50%/Ptop 100% | Ptop 5%/Ptop 10% | Ptop 50%/Ptop 100% | Ptop 5%/Ptop 10% | |
| Australia | 0.59 | 0.62 | 0.56 | 0.44 |
| Canada | 0.49 | 0.44 | 0.57 | 0.45 |
| China | 0.51 | 0.50 | 0.48 | 0.47 |
| EU | 0.36 | 0.49 | 0.51 | 0.41 |
| Germany | 0.38 | 0.57 | 0.55 | 0.49 |
| India | 0.48 | 0.33 | 0.46 | 0.36 |
| Japan | 0.24 | 0.55 | 0.33 | 0.45 |
| Singapore | 0.63 | 0.60 | 0.58 | 0.56 |
| South Korea | 0.46 | 0.41 | 0.38 | 0.44 |
| UK | 0.50 | 0.47 | 0.58 | 0.57 |
| USA | 0.47 | 0.62 | 0.58 | 0.56 |
Ptop x%, number of papers in top percentile x |
Overall, in Table 7 , in 11 out of 22 cases, the ratios are equal (deviations < 15%), while in the other cases, Ptop 50%/P is larger or lower than Ptop 5%/Ptop 10%, reproducing India and Japan in Figure 3. In graphene, in three countries: Germany, Japan, and the USA, Ptop 50%/P is lower than Ptop 5%/Ptop 10%, and in one country, India, Ptop 50%/P is larger than Ptop 5%/Ptop 10%. In solar cells, in two countries: Japan and South Korea, Ptop 50%/P is lower than Ptop 5%/Ptop 10%, and in three countries: Australia, Canada, and India, Ptop 50%/P is larger than Ptop 5%/Ptop 10%. In the EU, Ptop 50%/P is lower than Ptop 5%/Ptop 10% in graphene and higher in solar cells.
4 Discussion
The aim of this study was to explore when statistical data that can be easily obtained, such as Ptop 10%/P or Ptop 1%/P, can or cannot be used for research assessment. It has been firmly established that when the global ranks of local publications follow an ideal power law, the assessment with these statistical data is accurate (Rodríguez-Navarro & Brito, 2021); the challenge is that deviations occur (Rodríguez-Navarro, 2024b). To address this challenge, the use of journals provides several advantages. Probably, no country or institution can have a research success similar to that of papers published in Nature or Science, but these and similar journals provide clues for research evaluation that would be impossible to obtain with countries and institutions. Another hallmark of this study is the use of research topics. Different topics that are published in the same journals or are together in the same research field may have very different citation distributions, especially in the proportion of uncited papers (Table 1 ), which is a crucial datum in the analysis of research indicators. The effects of these uncited papers on indicators are more difficult to study in the mix of many topics, where internal compensations occur, than when the topics are studied independently.
4.1 Conformity with the ideal double rank power law
Analyses of percentile ratios across countries and research topics demonstrate that conformity with the ideal power law (Ptop 10%/P = Ptop 5%/Ptop 50% = Ptop 3%/Ptop 30% = Ptop 1%/Ptop 10%) is frequent. However, deviations from the power law, either with increasing or decreasing patterns of these serial ratios, are also frequent (Tables 2 and 3 ). For example, the EU shows increasing ratios in graphene but decreasing ratios in solar cells; the USA shows increasing ratios in graphene but constant ratios in solar cells; India shows increasing ratios in both topics; and Japan shows decreasing ratios in both topics. In these conditions, the comparison of countries with a single per-publication indicator of efficiency (e.g. Ptop 10%/P) is uncertain. According to double rank plots, countries’ comparisons will be reliable when deviations from the power law are not important (Figure 2 ), but impossible to perform with a single indicator when the deviations are important (Figure 3 ).
Deviations from the power law appear when there are significant differences between countries’ and global citation distributions (Rodríguez-Navarro, 2024b), especially with reference to the proportion of uncited papers (Tables 1-3). Possibly, in global and countries’ distributions, there is always an excess of uncited papers with reference to a lognormal distribution (Rodríguez-Navarro, 2024b). Figure 1 depicts the normal probability plot of the log-transformed number of citations (plus 1) in two topics, which suggests that most of the citation distribution could be modeled according to a lognormal distribution, but that the lower tail has an excess of lowly cited papers. However, it is worth noting that discretization of a continuous lognormal distribution of random numbers with a low μ parameter also produces an apparent excess of zeros because, in such continuous series, many numbers are less than 0.5. This implies that to test the lognormal distribution of citations, normal probability plots of the log-transformed number of citations must be performed in parallel with other types of analysis.
In graphene, the proportion of uncited papers in Nature Communications, Advanced Materials, Nanoscale, and Electrochimica Acta is lower than that in global papers, and the right extreme of the log-log double rank plot shows downward concavity, as shown in Figures 4 , 5 , and 6. The analysis of these figures suggests that the deviation of the double rank plots, namely, the degree of the curvature, depends on the difference in the lowly cited papers (zero, one, and two citations) between the journal and global citation distributions. However, the comparison of ACS Applied Materials & Interfaces and Scientific Reports on the topics of graphene and semiconductors (Figure 6 ) suggests that the maximum deviation seems to have a limit. In ACS Applied Materials & Interfaces, the curvature is similar in graphene and semiconductors, although there is a large difference in the proportion of uncited papers in these two topics (Table 1 ), whereas the proportion of uncited papers in both topics in this journal is similar (0.14% and 0.11%, Tables 6 and 4 , respectively).
Widely used percentile indicators (e.g. Ptop 10%/P) are not absolute measures of research success but relative measures because they are obtained by comparing the research of countries and institutions with global research. The results of this study indicate that when the citation distribution of a country or institution is very different from the global distribution, especially in the proportion of uncited papers, the double rank plot deviates from a power law. In these cases, research assessments cannot be performed using easy-to-obtain statistical data.
4.2 Not less than four indicators are necessary for the research assessment of countries
The translation of the conclusions reached with journals to countries warns against using the number of publications and another single indicator, e.g. Ptop 10%/P, for the evaluation of countries and institutions. Most current evaluations use this method, which may be highly misleading in some cases. A reasonable conjecture is that the method undervalues countries with high-technology industries (Japan, Germany, South Korea, USA, etc.) in those technological topics where they have global influence and overvalues countries where there is academic research that is not being applied by a competitive industry. The latter case is probably more frequent in research-leading universities (Rodríguez-Navarro, 2024b). Most of these deviations can be predicted from the proportion of uncited papers. In countries and institutions with research oriented toward technological improvements, the proportion of uncited papers is higher than the mean shown by global publications. Conversely, in countries and institutions dominated by academic research, the proportion of uncited papers is lower than the average of global publications. Consequently, in both cases, using P (total number of publications) to calculate the Ptop 10%/P or Ptop 1%/P ratios, and subsequently using the results in research assessments, will be misleading in many cases.
These considerations about academic and applied research and the proportion of lowly cited papers raise an interesting question regarding the evaluation of research efficiency. In principle, the ratio between applied and academic research is a structural characteristic of research systems that is not necessarily linked to the efficiency of each type of research. This point of view again leads to the simple conclusion that research efficiency cannot be measured with a single size-dependent indicator, which is an unquestionable datum, divided by the total number of papers. Further research is necessary to determine the most appropriate indicators. However, the indicators used in Table 7 can be obtained easily and can be used to characterize the bulk of research. A different issue is the contribution of pushing the boundaries of knowledge, which might depend on research elites that may not be visible when the bulk of papers is considered. This contribution can be easily measured from the ranks of the most cited papers (Rodríguez-Navarro & Brito, 2024). However, this is a size-dependent parameter that should be normalized to a size-independent measure to compare countries or institutions, which is a challenge if P cannot be used for this purpose. Abramo and D’Angelo (2016a, 2016b) criticized the use of common size-independent indicators from the point of view of research performance. The issue raised in the present study is different and refers to the misleading use of per-publication indicators as a measure of efficiency.
These results imply that a minimum of four indicators, either parametric or nonparametric, are necessary to describe a research system: (i) the size; (ii) the lower tail (the 50% least cited papers), which informs about the comparison of the research system in terms of lowly cited papers; (iii) the extreme of the upper tail, in order to find out the contribution to pushing the boundaries of knowledge (Rodríguez-Navarro & Brito, 2024); and (iv) an indicator for the 50% most cited papers. This last indicator might be used to determine the efficiency of the portion of the system that has an academic orientation pursuing the boundaries of knowledge.
5 Conclusions and implications
The use of a single size-independent indicator to describe the research output of countries and institutions is highly widespread among international and national agencies. The most frequent are Ptop 10%/P and Ptop 1%/P. This study demonstrates that these assessments and the corresponding rankings are correct in some cases but misleading in others. Consequently, the use of these indicators for research assessment creates drawbacks and confusion that conceal their benefits. The statement of Garfield and Welljams-Dorof (1992) - “Government policy-makers, corporate research managers, and university administrators need valid and reliable S&T indicators for a variety of purposes: for example, to measure the effectiveness of research expenditures, identify areas of strength and excellence, set priorities for strategic planning, monitor performance relative to peers and competitors, and target emerging specialties and new technologies for accelerated development” - defines a need that currently, more than 30 years after it was written, has not been met. Therefore, every effort should be made to find a solution to this challenge. The results of this study open an avenue of research to reach that solution.
Data availability statements
The raw bibliometric data were collected from Clarivate Analytics. A license is required to access the Web of Science database; therefore, the raw data used in this paper cannot be posted in a repository. However, the data analyzed in this study are available from the author upon request.