JDIS

Journal of Data and Information Science >

2025 , Vol. 10 >Issue 2: 40 - 60

DOI: https://doi.org/10.2478/jdis-2025-0013

Research Papers

A new approach to compare the scientific impact of scholars

  • Anand Bihari , 1, † ,
  • Sudhakar Tripathi 2 ,
  • Akshay Deepak 3 ,
  • P. Mohan Kumar 4
Expand
  • 1Department of Computational Intelligence, School of computer Science and Engineering, Vellore Institute of Technology, Vellore, Tamil Nadu -India
  • 2Department of Information Technology, Rajkiya Engineering College, Ambedkar Nagar, U.P. India
  • 3Department of Computer Science and Engineering, National Institute of Technology Patna. Bihar, India
  • 4Department of Database Systems, School of computer Science and Engineering, Vellore Institute of Technology, Vellore, Tamil Nadu -India
† Anand Bihari (Email: ; ).

Received date: 2024-09-19

  Revised date: 2024-12-21

  Accepted date: 2024-12-23

  Online published: 2025-01-20

Fold

Abstract

Purpose: Generally, the scientific comparison has been done with the help of the overall impact of scholars. Although it is very easy to compare scholars, but how can we assess the scientific impact of scholars who have different research careers? It is very obvious, the scholars may gain a high impact if they have more research experience or have spent more time (in terms of research career in a year). Then we cannot compare two scholars who have different research careers. Many bibliometrics indicators address the time-span of scholars. In this series, the h-index sequence and EM/EM’-index sequence have been introduced for assessment and comparison of the scientific impact of scholars. The h-index sequence, EM-index sequence, and EM’-index sequence consider the yearly impact of scholars, and comparison is done by the index value along with their component value. The time-series indicators fail to give a comparative analysis between senior and junior scholars if there is a huge difference in both scholars’ research careers.
Design/methodology/approach: We have proposed the cumulative index calculation method to appraise the scientific impact of scholars till that age and tested it with 89 scholars data.
Findings: The proposed mechanism is implemented and tested on 89 scholars’ publication data, providing a clear difference between the scientific impact of two scholars. This also helps in predicting future prominent scholars based on their research impact.
Research limitations: This study adopts a simplistic approach by assigning equal credit to all authors, regardless of their individual contributions. Further, the potential impact of career breaks on research productivity is not taken into account. These assumptions may limit the generalizability of our findings
Practical implications: The proposed method can be used by respected institutions to compare their scholars impact. Funding agencies can also use it for similar purposes.
Originality/value: This research adds to the existing literature by introducing a novel methodology for comparing the scientific impact of scholars. The outcomes of this research have notable implications for the development of more precise and unbiased research assessment frameworks, enabling a more equitable evaluation of scholarly contributions.

Key words： h-index; EM-index; EM’-index; h-index sequences; EM-index sequence; EM’-index sequence; Scientific comparison; Research impact

Cite this article

Anand Bihari , Sudhakar Tripathi , Akshay Deepak , P. Mohan Kumar . A new approach to compare the scientific impact of scholars[J]. Journal of Data and Information Science, 2025 , 10(2) : 40 -60 . DOI: 10.2478/jdis-2025-0013

1 Introduction

The scientometrics and bibliometrics indices have been used for faculty promotion, research award distribution, and approval of project fund (King, 1987). To do this, the comparison between scholars has been done with the help of single indices. Based on the comparison result, the things are decided. During the comparison of the scientific impact of scholars, the career of scholars has not been considered. In the research community, generally, the h-index (Hirsch, 2005) is used for scientific assessment and comparison between scholars. As we know that the h-index does not consider the career of the scholars. So, we cannot compare two scholars’ scientific impact whose research career is not similar. To consider the career of the scholar in comparison to the scientific impact of scholars, Liang (2006) introduced the h-index sequence. In this index, the author has computed the h-index value from the yearly citation count and gives a set of values that helps to know the yearly impact of scholars. In this index, the reverse-chronological order (current to first) of the research career was considered. In continuation of this, Egghe (2009) considered the forward direction of the research career (initial to current). Furthermore, Liu and Rousseau (2008) outlined 10 different set of index value, while Fred and Rousseau (2008) discussed the relationship between h-index sequence values and the power-law method. Next, Wu et al. (2011) and Liu and Yang (2014) performed the empirical study on h-index sequence based on Egghe’s sequence and proposed L-sequence. In continuation of this, Mahbuba and Rousseau (2013, 2016) presented the year based h-index for scientific assessment of scholars. All of the above indices consider the h-index as a basic measure to find the impact of scholars. As we know that the h-index considers only core citation count and leaves a huge amount of excess and tail citation count. To address this issue, Bihari and Tripathi (2018) proposed the year-based EM and EM’-index of scholars, while Bihari et al. (2020) proposed the EM-index sequence, which considers the year based citation count of scholars. The above-discussed indices considered the times series data of scholars but did not provide any efficient way to compare the scientific impact of scholars for the dissimilar career of scholars. This article addresses the mentioned issue and considers scholars’ cumulative year-wise citation count to compare the scholars’ impact on having different research careers.
In this article, the detailed literature review presented in Section 2 includes a thorough description of the h-index, EM-index and EM’-index. Then, we discuss the proposed methodology for comparing the scientific impact of scholars and also perform the empirical study on the 89 scholars’ citation data, which was used in Bihari and Tripathi (2018). Section 3 and Section 4 summarize the findings.

2 Literature review

In the field of scientific assessment of scholars, several assessment metrics have been designed with different parameters. However, the limited number of research addressed the issue while comparing the scientific impact of scholars. One of the prominent indexes, named h-index, has been used to assess and compare the scientific impact of scholars.
The h-index, proposed by Hirsch (2005), is: “The h-index of a scholar is h if h of his/her publications has at least h citations each and the rest of the publications may have h or less citations.”
As we know, the h-index gains a lot of attention due to its simplicity and ease of use. But it suffers from many limitations, especially in consideration of excess and tail citation count. To overcome the limitations of the h-index, several indices have been designed and reviewed (Alonso et al., 2009; Bihari et al., 2021; Bornmann et al., 2008; Bornmann et al., 2011; dos Santos Rubem & de Moura, 2015; Egghe, 2006a, 2006b; Huang & Chi, 2010; Norris & Oppenheim, 2010; Schreiber et al., 2012; Tol, 2009). In continuation with other indices, the EM-index has been designed by Bihari and Tripathi (2017); and is defined as: “The EM-index of a scholar is the square root of the sum of the component of the EM-index.” It is calculated as follows:
$E M=\sqrt{\sum_{a=1}^{k} E M_{a}} $
Here, k denotes the total number of components comprising the EM-index, with EM representing the consolidated EM-index value. The EM-index considers only the core citation count while the EM’-index (Bihari & Tripathi, 2017) considers both core and tail article citation count and also considers the importance of excess citation count. It is calculated as follows:
$E M^{\prime}=\sqrt{\sum_{a=1}^{k} E M_{a}^{\prime}}$
Notwithstanding the progress achieved so far, the above-discussed indices consider only scholars’ total citation count without the consideration of the career of the scholars. With consideration of the above-discussed indices, it is extremely hard to gauge the impact of scholars and also difficult to compare the scholar’s impact at a different stage of the career. To consider the total research career or year wise impact of the scholars, Mahbuba and Rousseau (2013, 2016), Liu and Yang (2014), and Bihari and Tripathi (2018) discussed the year-based approach for the scientific assessment of scholars. Mahbuba and Rousseau (2013, 2016) proposed the three-years-based h-index that are computed based on (i) year-wise citation count of all publications, (ii) Year-wise publication and their total citation count, and (iii) year-wise publication count. This index also does not help in comparing the scientific impact of scholars and also suffers from the same limitations as the h-index suffers. In this context, Bihari and Tripathi (2018) discussed the same methodology with the EM and EM’ and proposed the year-based EM and year-based EM’ with all three methods. The year-based EM and EM’-index consider both core and tail article’s citation count respectively that has not been considered in year-based h-index. But none of the year-based indices can differentiate the impact of scholars who do not have a similar research career. Liu and Yang (2014) examined the h-index sequence and suggested a new index known as the L-sequence in order to get around the problem of year-based indices. To calculate the scientific impact, the L-sequence takes into account a scholar’s whole research career. Consider a scholar who has authored m publications during their career to define L-sequence. Let the first publication year be y1 and the current year is yn. Then, the L-sequence of a scholar for kth year, denoted Lk, is the h-index value computed based on citation counts of all publications received in the kth year. Thus, the L-sequence is Ly1, Ly2, ………, Lyn.
The L-sequence is calculated using the h-index, but it ignores the effects of h-tail items and excessive citations. To overcome this limitation, the EM-index sequence and EM’-index sequence have been designed by the Bihari et al. (2020).
The above-discussed indices consider the overall index value or a single value to compare the scientific impact of scholars. If the scholars have a similar or equal number of research careers, then these methods can be used to compare scholars’ scientific impact. In an organization, the scholars’ careers are not identical or similar; in this case, we cannot compare their scientific impact by those indices. If the scholar is senior, then it is obvious he/she has a high index value compared to the scholars who have started their careers in recent years. And the comparison between senior and junior scholars never gives a comprehensive result. As a result, it is required career based comparison, and then only we can know the actual impact of both scholars at their same career stage. In this context, Fred and Rousseau (2008) considers the power-law method with the consideration of total citation count, the total number of publications and the number of collaborators and gives a new measure to compare the scientific impact of scholars. Egghe (2013) discussed the comparison of scholars with different careers and described the mathematical model for comparison of the scientific impact of scholars. Further, Harzing et al. (2014) criticize the comparison of scientific impact of scholars and proposed the new index called hIa-index. In this research, the author has considered the annual increment of the citation count of scholars, and the comparison has been done based on that. Next, Smith (2015) discussed the platinum h-index for scientific comparison of scholars. All indices, as mentioned earlier, consider the h-index for comparison of the scientific impact of scholars, which fails to account for the impact of excess and tail citation count. It is also very difficult to compute and analyze. This research highlights this problem and provides an alternative solution for comparing the scholars who do not have similar research careers.

3 Proposed method and discussion

Based on the discussion in Section 2, all year-based indices and the time-series indices are not much useful in comparison to the scientific impact of scholars who have different research careers because all of the above-mentioned indices consider only the overall impact of scholars. Also, the h-index has not helped in comparison because it is computed based on the total citation count of articles and left a huge amount of citations. In this context, we have designed a new methodology that significantly differentiates the scholarly impact of scholars.

3.1 Dataset description

In this article, we consider the 89 scholars’ citation data that was used in Bihari and Tripathi (2018). The dataset has been downloaded from the web of science database in the year 2017 with the keyword of “Scientometrics or Bibliometrics”. This dataset contains only those scholars’ data who have published at least one publication in the field of scientometrics. The statistics of the authors’ citation data are presented in Table 1.
Table 1. Statistics of the dataset (dataset ref. Bihari and Tripathi (2018)).
ID Name Starting Year First Citation Year Total Publication Total Citation Count Avg. Citation Total Career
1 Adamantios Diamantopoulos 2005 2007 55 1,974 35.89 13
2 Albert Zomaya 2006 2006 291 2,306 7.92 12
3 Alireza Abbasi 2006 2007 170 1,060 6.24 12
4 András Schubert 2006 2006 41 797 19.44 12
5 András Telcs 2000 2001 18 89 4.94 18
6 Andreas Thor 2007 2007 51 526 10.31 11
7 Andrew D. Jackson 2006 2007 26 326 12.54 12
8 Anne-Wil Harzing 2007 2008 47 1,333 28.36 11
9 Aric Hagberg 2002 2003 24 504 21.00 16
10 Barry Bozeman 2006 2007 64 1,177 18.39 12
11 Ben R Martin 2007 2008 25 405 16.20 11
12 Benny Lautrup 2006 2007 5 190 38.00 12
13 Berwin Turlach 2007 2008 16 73 4.56 11
14 Birger Larsen 2006 2006 48 200 4.17 12
15 Blaise Cronin 2006 2006 53 765 14.43 12
16 C Lee Giles 2006 2008 91 574 6.31 12
17 Carlos Pecharroman 2006 2007 36 708 19.67 12
18 Caroline S. Wagner 2008 2009 15 320 21.33 10
19 Christoph Bartneck 2007 2009 63 477 7.57 11
20 Claes Wohlin 2006 2007 68 674 9.91 12
21 Clint D. Kelly 2006 2007 35 525 15.00 12
22 Dimitrios Katsaros 2006 2008 54 680 12.59 12
23 Egghe Leo 1997 1998 181 2,549 14.08 21
24 Elizabeth A. Corley 2006 2007 37 692 18.70 12
25 Erhard Rahm 2006 2007 50 622 12.44 12
26 Fiorenzo Franceschini 2006 2009 66 374 5.67 12
27 Fred Y. 2006 2007 43 227 5.28 12
28 Gad Saad 2006 2006 27 308 11.41 12
29 Gangan Prathap 2006 2008 105 353 3.36 12
30 Gary M. Olson 2007 2013 6 13 2.17 11
31 Gerhard Woeginger 2006 2006 124 618 4.98 12
32 Guang-Hong Yang 2006 2007 424 3,753 8.85 12
33 Heidi Winklhofer 2006 2008 12 138 11.50 12
34 Hendrik P. van Dalen 2006 2007 23 326 14.17 12
35 Henk F. Moed 2007 2008 37 798 21.57 11
36 Herbert Van de Sompel 2006 2006 5 45 9.00 12
37 Hirsch J. E. 1989 1990 121 5,963 49.28 29
38 James Moody 2006 2007 52 690 13.27 12
39 Jayant Vaidya 2006 2006 39 1,027 26.33 12
40 Jerome Vanclay 2006 2006 42 1,151 27.40 12
41 Johan Bollen 2006 2006 33 1,449 43.91 12
42 John Irvine 2000 2002 267 4,530 16.97 18
43 Judit Bar-Ilan 2006 2007 72 926 12.86 12
44 Kène Henkens 2007 2008 57 847 14.86 11
45 Loet Leydesdorff 2006 2007 232 4,624 19.93 12
46 Lokman Meho 2006 2006 16 907 56.69 12
47 Luca Mastrogiacomo 2009 2009 48 244 5.08 9
48 Ludo Waltman 2006 2007 69 1,899 27.52 12
49 Lutz bornmann 2006 2006 234 3,534 15.10 12
50 Maisano, Domenico A. 2009 2010 5 75 15.00 9
51 Marek Kosmulski 2005 2006 64 817 12.77 13
52 Maria Bordons 2007 2008 43 552 12.84 11
53 Mark Ffine 2006 2007 12 158 13.17 12
54 Mark Newman 2003 2006 213 2,475 11.62 15
55 Mathieu Ouimet 2007 2008 40 467 11.68 11
56 Matjaž Perc 2006 2006 215 9,754 45.37 12
57 Matthew O. Jackson 2006 2007 56 1,559 27.84 12
58 Mauno Vihinen 2002 2006 107 2,625 24.53 16
59 Michael Jennions 2006 2007 98 2,445 24.95 12
60 Michael L. Nelson 2005 2007 45 52 1.16 13
61 Miguel A. García-Pérez 2005 2007 70 729 10.41 13
62 Morten Schmidt 2009 2010 104 1,167 11.22 9
63 Nees Jan van Eck 2006 2007 61 1,664 27.28 12
64 Nils T. Hagen 2008 2009 11 145 13.18 10
65 Olle Persson 2006 2008 18 153 8.50 12
66 Paul Wouters 2006 2007 30 406 13.53 12
67 Peter Jacso 2006 2006 69 677 9.81 12
68 Raf Guns 2009 2009 27 158 5.85 9
69 Raj Kumar Pan 2006 2007 26 463 17.81 12
70 Richard S J Tol 1999 2001 174 3,327 19.12 19
71 Roberto Todeschini 2006 2007 51 1,415 27.75 12
72 Robin hankin 2007 2008 15 149 9.93 11
73 Rodrigo Costas 2007 2008 49 717 14.63 11
74 Ronald Rousseau 1993 1994 546 9,905 18.14 25
75 Ruediger mutz 2007 2007 43 968 22.51 11
76 Santo Fortunato 2006 2007 56 8,441 150.73 12
77 Serge Galam 2006 2007 30 480 16.00 12
78 Sergio Alonso 2006 2007 79 1,325 16.77 12
79 Steve Lawrence 2006 2006 12 118 9.83 12
80 Sune Lehmann 2006 2006 18 832 46.22 12
81 Terttu Luukkonen 2007 2010 6 78 13.00 11
82 Vicenç 2006 2007 148 1,460 9.86 12
83 Walter W (Woody) Powell 2006 2007 12 591 49.25 12
84 Werner Marx 2006 2008 61 635 10.41 12
85 Wolfgang Glänzel 2006 2006 95 1,268 13.35 12
86 Yannis Manolopoulos 2006 2007 89 850 9.55 12
87 Ying Ding 2005 2007 517 3,965 7.67 13
88 Yu-Hsin Liu 2006 2007 28 159 5.68 12
89 Yvonne Rogers 2003 2004 47 539 11.47 15
From Table 1, it can be seen the average research career is 12 years, and a total of 21 authors have a lesser research career than the average research career. The research career is calculated from the year of first publication to 2017 (including both). The used data contains the citation information till 2017. Author Luca Mastrogiacomo (ID=47), Maisano, Domenico A. (ID=50), Morten Schmidt (ID=62) and Raf Guns (ID=68) have equal research career that is 9 and also the lowest research career. While author Hirsch J. E. (ID=37) is the senior scholar with 29 years of research career. Most of the scholars start earning the citation by the same year or after 1 year of their first publication. Author Gary M. Olson (ID=30) got the first citation after 6 years of their first publication. According to publication count, author Ronald Rousseau (ID=74) has published a total of 546 articles on the publication career of 25 years with a total of 9,905 citation count. If we compare this author with Hirsch J. E. (ID=37) who has 29 years of their research career and published 121 articles with 5963 citation count, then we can say that total career does not matter in the scientific assessment of scholars. Similarly, if we compare author Ronald Rousseau (ID=74) and Matjaž Perc (ID=56), then we can see the total research career and publication count is just double for Ronald Rousseau (ID=74). But their total citation count is just above Matjaž Perc (ID=56). And also, the average citation count is very less than the author Matjaž Perc (ID=56). If we consider the average citation count, then author Santo Fortunato (ID=76) has a high average citation count, i.e. 150.73 with a 12-year research career and 56 publications. After this author, the maximum average citation count is 56.69 for author Lokman Meho (ID=46) with a 12-year research career and 16 publication count. The above discussion considers only the citation count, total publication count, average citation count, and total career length of the scholars that do not discriminate the impact of scholars. If we consider the h-index, EM-index, and EM’-index, then we get the impact of scholars based on their total citation count. In this case, the author has a high research career may have a high index value also and they are not comparable with another scholar who has a relatively lesser impact (h-index, EM-index and EM’-index of scholars is shown in Table 2).
Table 2. h-index, EM-index and EM’-index of all scholars (dataset ref. Bihari and Tripathi (2018)).
ID h-index EM-index EM’-index ID h-index EM-index EM’-index
1 23 17.69 21.47 46 9 12.65 19.13
2 25 10.82 15.36 47 8 4.24 6.86
3 16 8.12 11.79 48 24 12.25 15.78
4 13 10.15 15.43 49 34 13.49 16.40
5 4 4.69 5.20 50 4 4.80 5.66
6 11 8.43 9.33 51 10 13.08 13.67
7 5 8.37 11.62 52 13 8.12 12.41
8 20 10.49 16.16 53 5 5.57 9.17
9 11 9.27 12.21 54 28 11.40 17.18
10 16 11.31 12.12 55 11 7.75 8.72
11 11 7.94 8.31 56 56 19.34 26.98
12 3 1.00 2.24 57 20 12.25 13.42
13 5 3.16 4.36 58 24 16.79 17.72
14 8 4.47 6.32 59 23 16.64 17.92
15 13 10.10 12.61 60 4 3.32 4.00
16 16 6.24 8.37 61 17 6.24 8.89
17 13 9.59 11.31 62 14 11.87 16.82
18 7 10.15 11.62 63 22 12.25 15.78
19 8 7.87 13.11 64 7 5.92 6.40
20 14 7.35 9.38 65 6 6.16 7.07
21 12 7.87 10.58 66 9 9.06 10.82
22 12 11.40 13.56 67 14 8.54 9.59
23 20 15.39 24.47 68 7 4.90 6.16
24 15 8.19 9.06 69 12 7.94 8.31
25 13 8.94 9.64 70 33 13.19 15.87
26 10 5.74 8.06 71 17 13.42 14.21
27 8 4.80 6.48 72 6 5.57 7.35
28 10 6.78 8.66 73 15 8.12 12.41
29 9 6.08 8.66 74 47 16.00 26.83
30 2 1.73 3.16 75 15 9.64 13.53
31 13 6.56 9.80 76 27 35.44 49.92
32 32 11.62 18.00 77 11 10.68 12.37
33 6 5.48 5.74 78 14 15.81 16.06
34 11 6.40 7.14 79 5 6.16 6.24
35 16 9.11 14.21 80 8 11.62 22.74
36 4 3.46 4.24 81 5 4.36 5.20
37 28 35.30 51.08 82 14 15.33 23.04
38 14 8.12 12.17 83 8 11.31 12.41
39 12 13.67 18.08 84 15 6.93 8.66
40 17 12.29 13.64 85 20 10.15 15.43
41 12 13.67 25.53 86 15 10.30 11.36
42 41 12.37 16.88 87 31 10.77 18.47
43 15 10.58 14.63 88 7 5.48 5.83
44 16 8.54 9.70 89 12 7.75 9.43
45 38 11.83 17.12
From Table 2, we can get only the overall index value of each scholar that does not help us to discriminate the performance of scholars. The high h-index, EM-index, and EM’-index value indicates the prominent scholars. If we consider the author Ronald Rousseau (ID=74) and author John Irvine (ID=42), then we find that first author took total 25 years to gain 47 h-index value. While the second author took a total of 18 years to gain 41 h-index value. As a result, the first author is more prominent than the second because his h-index value is more than the second one. However, the first author index value at the 18th year of their research career (that is, the current total research career in the year of the second author) is 33 only. So, let’s consider the first 18 years for comparison. Then we can say that the second author is more prominent than the first one, and if the second author performs with the same consistency, then he might get the higher index value in the 25th year of their research career (the current research career of the first author). The above discussion states that the existing methodology cannot help us to compare the scientific impact of senior and junior scholars and also not help us to identify future prominent scholars. To make a clear comparison of any career year scholars, the comparison between scholars should be done from the root of the citation year, as described below.

3.2 Proposed method

In the year based indices, the year-wise individual impact of scholars has taken into consideration and computed the index value based on the citation count earned in the respective year. While this methodology allows for a comparison of the year-wise impact of scholars, it does not effectively compare the scientific impact of scholars who have different research careers. Instead of considering year-wise impact, the cumulative citation count could be effective to compute the overall impact to date. This methodology also helps in comparing the scientific impact of scholars and for the prediction of future prominent scholars. To demonstrate the proposed method, we have considered the publication and citation history of Author Luca Mastrogiacomo, as shown in Table 3.
Table 3. Publication and citation history of Author Luca Mastrogiacomo (ID=47).
Article 2009 2010 2011 2012 2013 2014 2015 2016 2017
1 0 0 0 0 9 18 28 39 42
2 2 9 11 11 11 15 17 18 18
3 0 0 0 0 8 13 14 17 17
4 1 4 6 6 7 11 11 15 15
5 0 0 1 3 4 8 11 12 12
6 0 0 0 0 0 2 5 11 11
7 0 2 4 4 5 6 7 8 9
8 0 0 0 0 0 0 0 8 8
9 0 0 0 0 0 0 0 7 8
10 0 0 0 0 0 0 3 8 8
11 0 1 2 3 5 7 7 8 8
12 0 0 0 0 0 0 2 6 7
13 0 0 0 0 0 0 0 7 7
14 0 0 0 0 0 0 2 6 7
15 0 2 3 4 4 5 5 7 7
16 0 0 0 0 2 5 6 7 7
17 1 2 3 3 5 5 7 7 7
18 0 1 2 3 4 4 4 6 6
19 0 0 0 0 0 0 0 4 5
20 0 0 0 0 0 0 0 5 5
21 0 0 0 0 0 2 2 4 5
22 0 0 0 0 0 0 0 1 3
23 0 0 0 0 0 0 0 2 3
24 0 0 0 0 0 0 0 2 2
25 0 0 0 0 0 0 0 2 2
26 0 0 0 0 0 0 0 2 2
27 0 0 0 0 0 0 0 1 2
28 0 0 0 0 0 1 1 2 2
29 0 0 0 0 0 2 2 2 2
30 0 0 0 0 2 2 2 2 2
31 0 0 0 0 0 0 0 0 1
32 0 0 0 0 0 0 1 1 1
33 0 0 0 0 0 0 0 1 1
34 0 0 0 0 0 0 0 1 1
35 0 0 0 0 0 1 1 1 1
h 1 2 3 4 5 6 7 8 8
EM 1 2.24 2.45 2.65 3 4 4.12 4.24 4.24
EM’ 1.73 3.16 3.46 3.46 4.24 5.1 5.83 6.78 6.86
Table 3 indicates the publication and their corresponding citation count earned till the respective year. The value in the column headed with 2010 indicates the total citation count earned by the publication to date, which is the sum of the citation count earned in 2009 and 2010. Every column of data represents the cumulative citation count to the respective year of the particular article. The column headed with 2017 (dataset contains the data till year 2017) indicates the total citation count of that article. The value given in the last three rows named h, EM and EM’ shows the respective year index value. That means the h-index value is 2 indicating their h-index in the year 2010. If we compute the index value based on this method, then we can easily know the index value of scholars at their respective career age. After that, we have to compare the impact of scholars; then only we can know the impact of scholars at their respective research age. Based on this comparison, we can decide the future prominent scholars. The proposed method also provides the year wise cumulated index value that helps to know that the index value of scholars at the particular age of their career. The validation of proposed method is given in discussion Section 3.3.

3.3 Discussion

In this section, we discuss the impact of proposed method. Section 3.1 discussed about the dataset and computed the average citation count, total career, and the number of years taken for the first citations. Section 3.2 discussed the proposed method of comparison of scientific impact of scholars. Our data set contains data up to the year 2017. We have computed the h-index, EM-index, and EM’-index for all authors using the cumulative citation count. The every year index value indicates the index value till that year, not the particular year index value as computed in Bihari et al. (2020). Then we can easily discriminate the impact of scholars.
For clarity of the proposed method, we have considered the citation impact and growth of authors ID 14, 19, 27, 47, 80, and 83. These authors have equal h-index values (i.e., 8), but they have different research careers, with durations of 12, 11, 12, 9, 12, and 12 years, respectively (as shown in Tables 1 and 2). According to the general methodology, all authors are equivalent, but it can be seen that the author ID=47 gains equal h-index value in the lesser time than the others. So, the author ID=47 should be prominent among them.
For more clarity about the proposed method, we have considered the author who has a similar h-index value but not a similar career. First, we have considered the last five year data (h-index, EM-index and EM’-index value) for analysis and found that it is almost similar to the consolidated index value. After that, we have made a comparative analysis from the root of the publication year (First year of publication). The comparative analysis of the Authors ID 37, 54, and 2 for the last five years are shown in Figure 1. The same difference can be observed in all parts of the Figure 1. This happens due to a long research career. This type of comparison will always reward the senior scholars and is not good for upcoming scholars. As a result, this type of comparison can not find a prominent actor in the community. Next, we have made a comparative analysis of scholars based on the proposed methods shown in Figure 2.
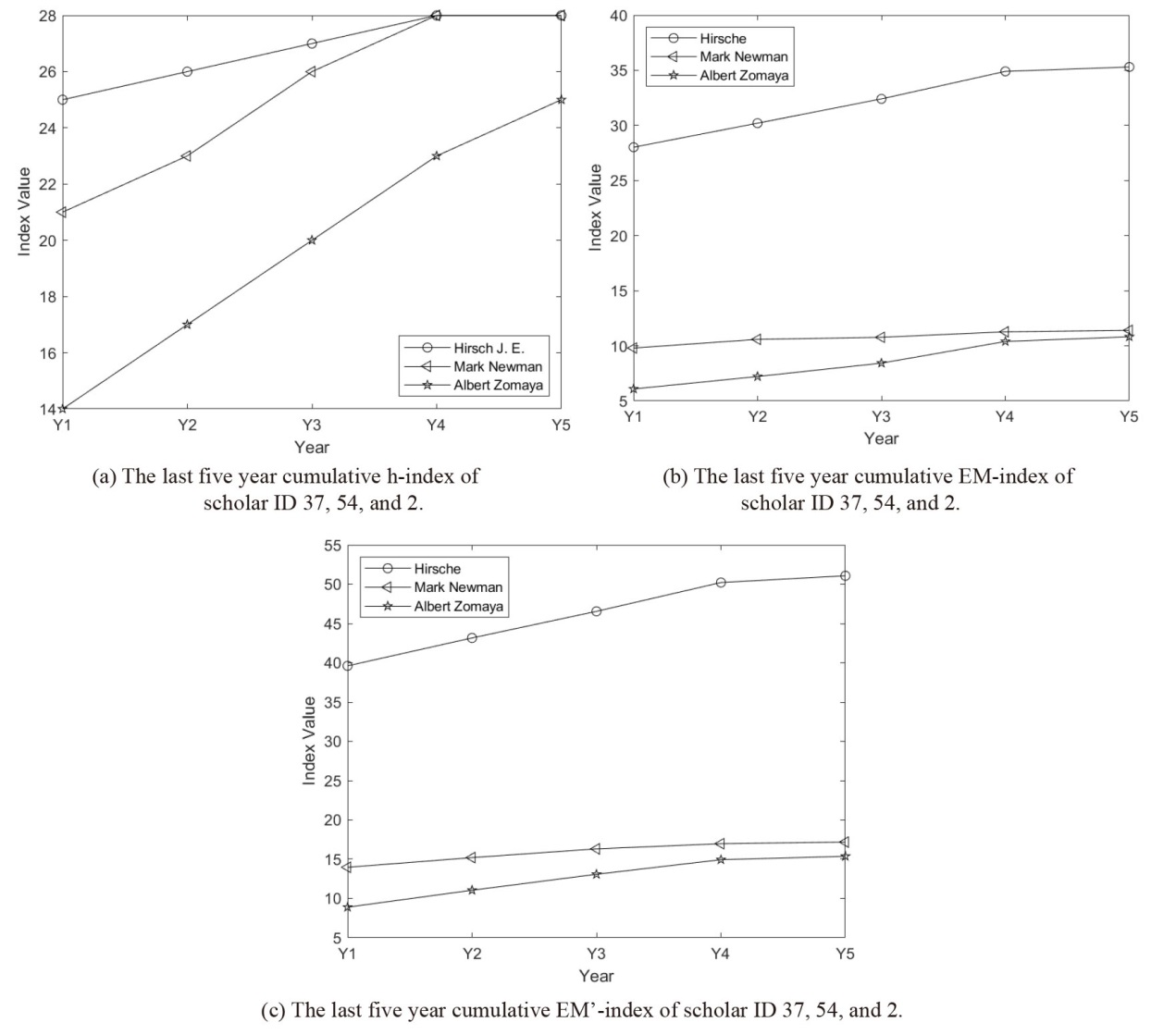
Figure 1. The last five year cumulative h-index, EM-index, and EM’-index of scholar ID 37, 54, and 2.
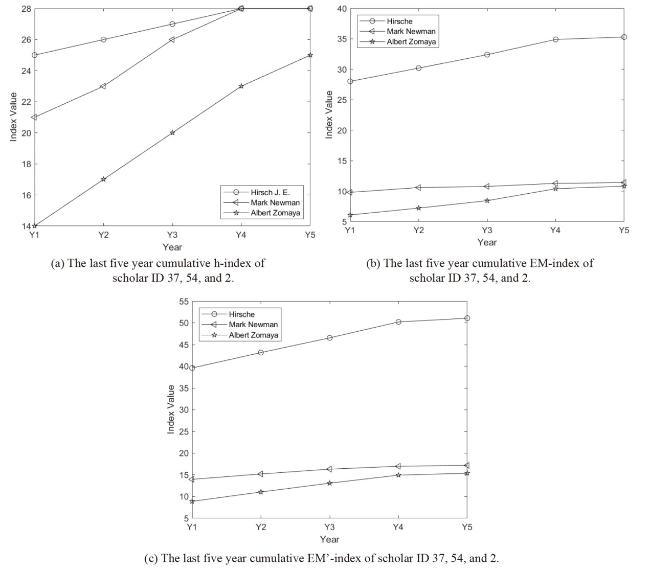
Figure 2. The cumulative h-index, EM-index, and EM’-index of scholar ID 37, 54, and 2.
Figure 2 shows the comparative analysis of cumulative h-index, EM-index, and EM’-index of scholar (ID=37) Hirsch, (ID=54) Mark Newman and (ID=2) Albert Zomaya. From Figure 2(a), it can be seen that the scholar Hirsch (37) and Mark Newman (54) having equal h-index value (i.e, 28), but the speed of the growth of index has huge difference. Author Hirsch took 28 years to gain this index value; however, the author Mark Newman took only 12 years to gain the similar index value. Author Albert Zomaya took a total of 12 years to gain an h-index value of 25, which is very near the h-index value of these two scholars. If we compare all scholars at a similar age of their research career (i.e., 12), their h-index value has a significant difference. Hirsch has only 8 h-index values at this career stage, which is very less than the author Mark Newman and Albert Zomaya. Similar difference can be seen in Figure 2(b) and Figure 2(c) with respect to EM and EM’-index. This analysis says that the author Mark Newman and Albert Zomaya are more prominent than Hirsch. The average growth of the h-index of author Hirsch is 1; however, the average growth of the h-index is 2.33 and 2.08, respectively, for authors Newman and Albert. If authors Newman and Albert index value increases with the same average, then the index value at the 28th year will be 65.33 and 58.33, respectively, and they are much higher than the Hirsch index value. Based on this comparison, we can predict future prominent scholars. To validate the proposed comparison method, we have performed another critical analysis of four scholars with the same h-index value and a different research career. The critical analysis of these four scholars is shown in Figure 3.
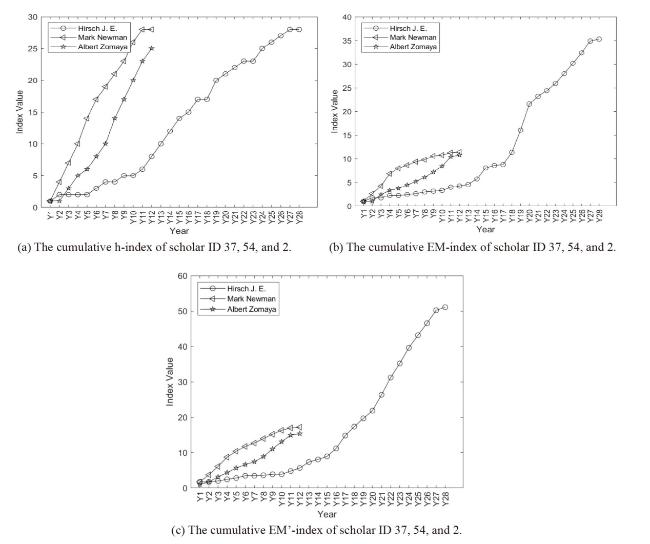
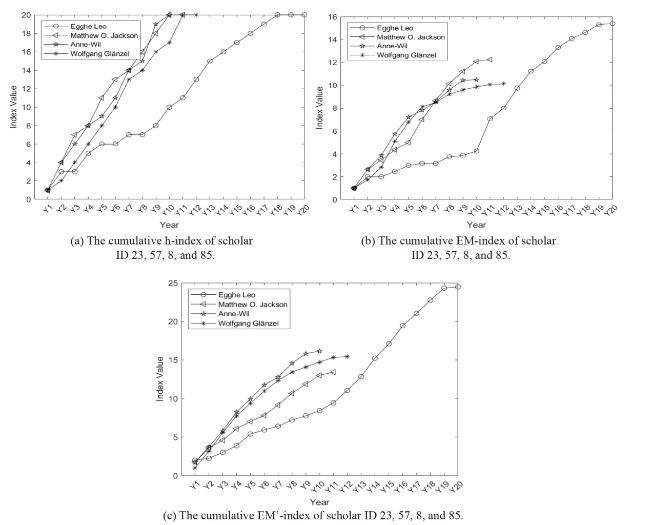
Figure 3. The cumulative h-index, EM-index, and EM’-index of scholar ID 23, 57, 8, and 85.
A similar difference can be observed in the Figure 3 and found that all author has equal h-index value but the period of getting this index is different (Figure 3a). Author Egghe Leo (ID=23) took 21 years to gain 20 h-index value. While author Matthew O. Jackson (ID=57) took 11 years, Anne-Wil (ID=8) took 10 years, and Wolfgang Glänzel (ID=85) took a total of 12 years to gain the h-index value of 20. If we consider only index value, then all have equal index value, but their index growth is different. The average growth of scholars is 0.95, 1.82, 2, and 1.67, respectively. As a result, author Anne-Wil is a prominent scholar than others in the group because he took less time to gain the equal index value and their average growth is also high. If these authors maintain the same consistency, then their index value in their 21st year of a research career will be 38, 42, and 35 for Matthew O. Jackson, Anne-Wil, and Wolfgang Glänzel, respectively. That is much more than the h-index value of Egghe at their research career of 21st year. The similar behaviour can be observed in the Figure 3(b) and 3(c). To provide more clarity in comparison, we have made one more critical review on two scholars whose index value is very close but have a huge difference between their careers. The next critical example is shown in Figure 4.
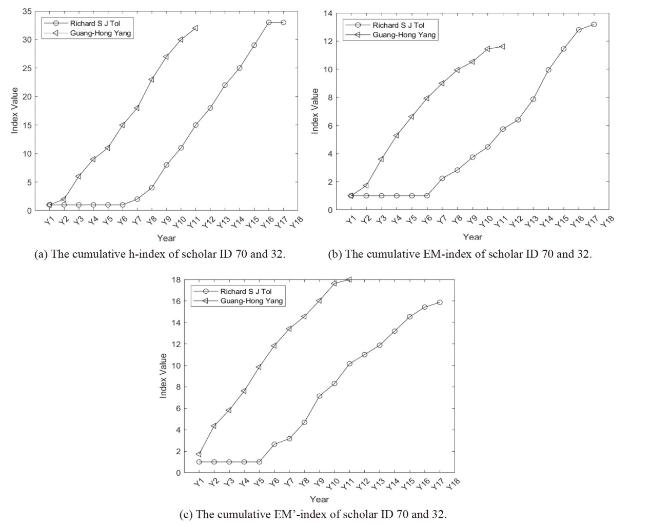
Figure 4. The cumulative h-index, EM-index, and EM0-index of scholar ID 70 and 32.
Figure 4 shows the comparative analysis of author Richard S J Tol (ID=70) and Guang-Hong Yang (ID=32) and found a similar pattern. In this example, the first author h-index value is 33 and took 18 years, while the second author h-index value is 32 (i.e., just below the first author h-index values) and took only 11 years. If the second author performs with the same consistency, then at the 18th year of their research career, his h-index value will be 52.36. As a result, Guang-Hong Yang is more prominent than Richard S J Tol. The similar behaviour can be observed with respect of EM and EM’-index shown in Figure 4(b) and 4(c).
Nowadays, it is common to see researchers working in more than one specialization at a given point in their careers. To validate the proposed comparison, we conducted experiments specific to scientometrics domain. For this, we have keywords ‘scientometrics’ or ‘bibliometrics’ and randomly selected 19 authors’ citation data. We have computed the result and compare the result only with the scientometrics papers. Statistics of the randomly selected author data is shown in Table 4.
Table 4. Comparative statistics of 19 randomly selected scholar data with scientometric publications only.
Whole Data Scientometrics Only
Sl. No Name Starting Year First Citation Year Total Pub Toatl Citation Count Avg. Citation Total Career Starting Year First Citation Year Total Pub Toatl Citation Count Avg.
Citation		 Total Career
1 Caroline S. Wagner 2008 2009 15 320 21.33 10 2008 2009 11 299 27.18 10
2 Christoph Bartneck 2007 2009 63 477 7.57 11 2010 2011 5 84 16.8 8
3 Egghe Leo 1997 1998 181 2,549 14.08 21 1998 1998 83 1,943 23.41 20
4 Fiorenzo Franceschini 2006 2009 66 374 5.67 12 2006 2009 32 185 5.78 12
5 Fred Y. 2006 2007 43 227 5.28 12 2006 2007 35 208 5.94 12
6 Gad Saad 2006 2006 27 308 11.41 12 2006 2006 2 82 41 12
7 Gangan Prathap 2006 2008 105 353 3.36 12 2006 2007 43 206 4.79 12
8 Hirsche 1989 1990 121 5,963 49.28 29 2005 2005 4 3,007 751.75 13
9 Loet Leydesdorff 2006 2007 232 4,624 19.93 12 2006 2007 167 3,280 19.64 12
10 Luca Mastrogiacomo 2009 2009 48 244 5.08 9 2012 2013 14 69 4.93 6
11 Ludo Waltman 2006 2007 69 1,899 27.52 12 2007 2008 57 1,727 30.30 11
12 Lutz bornmann 2006 2006 234 3,534 15.10 12 2006 2006 227 3,422 15.07 12
13 Marek Kosmulski 2005 2006 64 817 12.77 13 2009 2010 13 56 4.31 9
14 Miguel A. 2005 2007 70 729 10.41 13 2009 2009 8 107 13.375 9
15 Peter Jacso 2006 2006 69 677 9.81 12 2006 2006 69 677 9.81 12
16 Raf Guns 2009 2009 27 158 5.85 9 2009 2009 27 158 5.85 9
17 Richard S J Tol 1999 2001 174 3,327 19.12 19 2008 2008 8 142 17.75 10
18 Ronald Rouseau 1993 1994 546 9,905 18.14 25 1998 1999 78 1,401 17.96 20
19 Wolfgang Glänzel 2006 2006 95 1,268 13.35 12 2006 2006 61 945 15.49 12
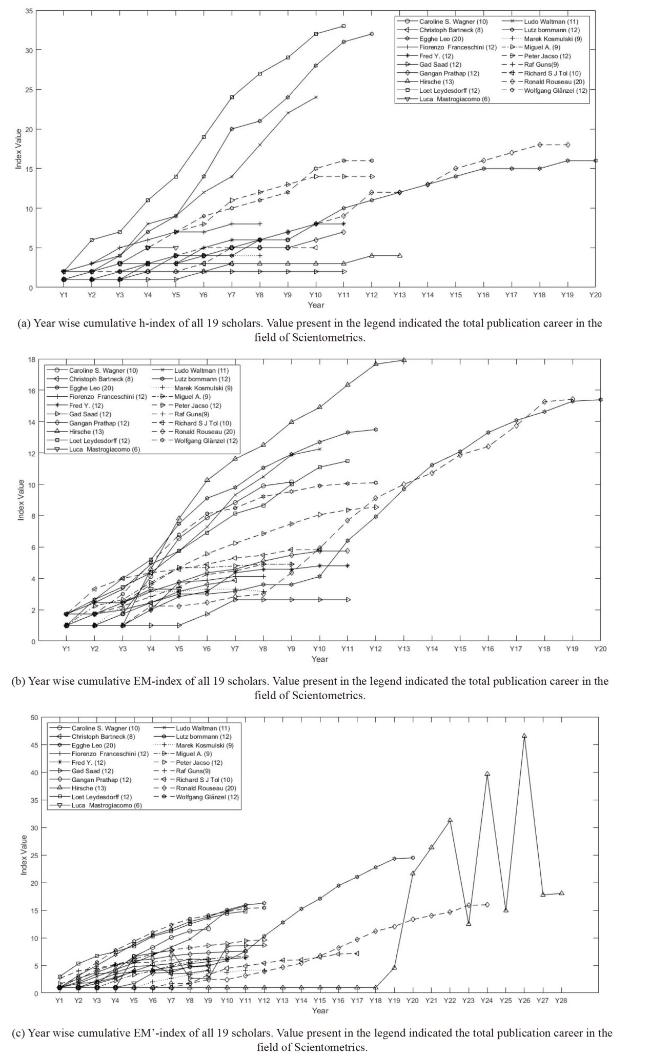
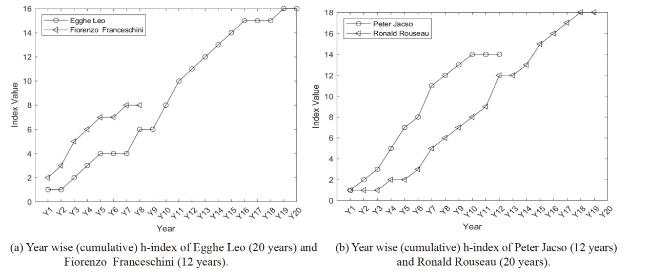
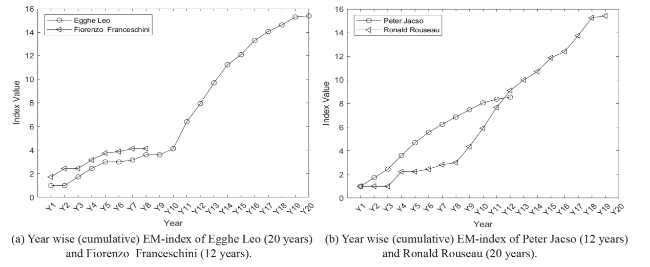
From the Table 4, it can clearly see that the average citation of scholars is increased in most cases. Next, we have computed the cumulative h-index, EM-index and EM’-index of all these 19 scholars and have significant difference in result. To demonstrate the proposed comparison technique we have selected citations of these 19 authors in the field of scientometrics and found the similar pattern. The proposed comparison with h-index, EM-index and EM’-index is shown in Figure 5.
Figure 5. The cumulative h-index, EM-index and EM’-index for 19 randomly selected scholars.
From the Figure 5, we can clearly see the citation impact of junior scholars is high as compare to the senior scholars in their first N year of their career. If the junior scholars perform with same consistency then their citation impact will be high at the age of senior scholars. If we see the performance of scholar Egghe Leo and Ronald Rouseau, then we can see that performance of both scholars is similar, because both having same academic career and their primary research domain is scientometrics. But if we compare the result with Loet Leydesdorff, Ludo Waltman, and Lutz bornmann, then we can see the clear difference between their impact. These three scholars citation impact is much better than the Egghe Leo and Ronald Rouseau. Therefore, we can conclude that the proposed comparison method is best suited to identify the future prominent scholars. In order to provide a nuanced evaluation of the proposed comparison method, we have made a personalized comparative study shown in Figure 6.
Figure 6. Year wise cumulative h-index of scholars.
Form the Figure 6(a), we can see the clear difference in the h-index of scholars Egghe Leo and Fiorenzo Franceschini. Scholar Fiorenzo has lesser research career than the Egghe Leo but have higher impact in first N year of research career. Similar observation found in the Figure 6(b). Further we have extended our analysis by performing a comparative analysis with EM-index and EM’-index. The result of this comparison is given in Figure 7 and 8 that endorse our initial findings and demonstrate the similar pattern and observation across these metrics.
Figure 7. Year wise cumulative EM-index of scholars.
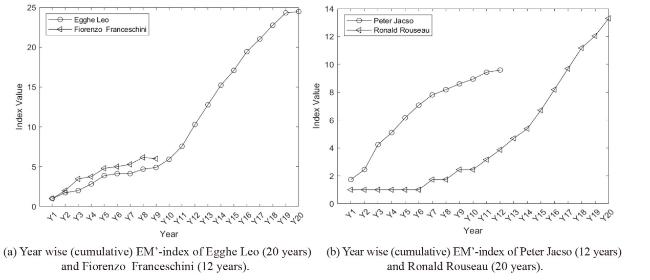
Figure 8. Year wise cumulative EM’-index of scholars.
From the above discussion, it can be observed that the traditional comparison methods help only to compare the scientific impact of scholars with respect to the citation count and always help senior scholars, which is not fair. The proposed comparison method helps us to make a fair comparison between scholars at any age of their research career. Also, it helps us to identify the prominent scholars based on their previous impact.

4 Conclusion

In the scientific comparison of scholars, the current index value is generally used, and the current index value is typically higher for senior scholars than for junior scholars. In comparison, all methods consider the same methodology that helps only senior scholars and does not help us in finding prominent scholars. Suppose we compare two scholars, one who is at the age of their retirement and the other at the beginning of their career. Then traditional method rewards to the scholar who is at the age of retirement and ignores young talent. Our proposed method compares the impact of scholars from the origin of their careers. That helps us to identify --- “What is the actual impact of a senior scholar at the age of the junior scholars?” and the comparison is made with respect to their impact at the same age of their career. The proposed method has been validated using 89 scholars data and has proven effective in distinguishing scholars' performance and predicting prominent scholars.

Author contributions

Anand Bihari (anand.bihari@vit.ac.in): Conceptualization (Equal), Data curation (Equal), Formal analysis (Equal), Investigation (Equal), Methodology (Equal), Resources (Equal), Software (Equal), Validation (Equal), Visualization (Equal), Writing - original draft (Equal), Writing - review & editing (Equal);
Sudhakar Tripathi (p.stripathi@gmail.com): Conceptualization (Equal), Methodology (Equal), Project administration (Equal), Supervision (Equal), Validation (Equal), Writing - original draft (Equal), Writing - review & editing (Equal);
Akshay Deepak (akshayd@nitp.ac.in): Conceptualization (Equal), Formal analysis (Equal), Project administration (Equal), Supervision (Equal), Validation (Equal), Writing - review & editing (Equal);
P. Mohan Kumar (pmohankumar@vit.ac.in): Validation (Equal), Visualization (Equal), Writing - review & editing (Equal).

Data availability statement

The data that support the findings of this study are available from the corresponding author, [Anand Bihari], upon reasonable request.

Declaration of interests

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

References

Publishing order | Descend order by publishing year | Descend order by cited within
[1]
Alonso, S., Cabrerizo, F. J., Herrera-Viedma, E., & Herrera, F. (2009). h-Index: A review focused in its variants, computation and standardization for different scientific fields. Journal of informetrics, 3(4), 273-289.

[2]
Bihari, A., & Tripathi, S. (2017). EM-index: a new measure to evaluate the scientific impact of scientists. Scientometrics, 112(1), 659-677.

[3]
Bihari, A., & Tripathi, S. (2018). Year based EM-index: a new approach to evaluate the scientific impact of scholars. Scientometrics, 114(3), 1175-1205.

[4]
Bihari, A., Tripathi, S., & Deepak, A. (2021). A review on h-index and its alternative indices. Journal of Information Science, 01655515211014478.

[5]
Bihari, A., Tripathi, S., Deepak, A., & Kumar, P. (2020). EM-and EM’-index sequence: construction and application in scientific assessment of scholars. Measurement: Interdisciplinary Research and Perspectives, 18(3), 142-157.

[6]
Bornmann, L., Mutz, R., & Daniel, H. D. (2008). Are there better indices for evaluation purposes than the h index? A comparison of nine different variants of the h index using data from biomedicine. Journal of the American Society for Information Science and technology, 59(5), 830-837.

[7]
Bornmann, L., Mutz, R., Hug, S. E., & Daniel, H. D. (2011). A multilevel meta-analysis of studies reporting correlations between the h index and 37 different h index variants. Journal of Informetrics, 5(3), 346-359.

[8]
dos Santos Rubem, A. P., & de Moura, A. L. (2015). Comparative analysis of some individual bibliometric indices when applied to groups of researchers. Scientometrics, 102(1), 1019-1035.

[9]
Egghe, L. (2006a). An improvement of the h-index: The g-index. ISSI newsletter, 2(1), 8-9.

[10]
Egghe, L. (2006b). Theory and practise of the g-index. Scientometrics, 69(1), 131-152.

[11]
Egghe, L. (2009). Mathematical study of h-index sequences. Information Processing & Management, 45(2), 288-297.

[12]
Egghe, L. (2013). On the correction of the h-index for career length. Scientometrics, 96(2), 563-571.

[13]
Fred, Y. Y., & Rousseau, R. (2008). The power law model and total career h-index sequences. Journal of Informetrics, 2(4), 288-297.

[14]
Harzing, A. W., Alakangas, S., & Adams, D. (2014). hIa: An individual annual h-index to accommodate disciplinary and career length differences. Scientometrics, 99(3), 811-821.

[15]
Hirsch, J. E. (2005). An index to quantify an individual’s scientific research output. Proceedings of the National academy of Sciences, 102(46), 16569-16572.

[16]
Huang, M. H., & Chi, P. S. (2010). A comparative analysis of the application of h-index, g-index, and a-index in institutional-level research evaluation. Journal of Library and Information Studies, 8(2), 1-10.

[17]
King, J. (1987). A review of bibliometric and other science indicators and their role in research evaluation. Journal of information science, 13(5), 261-276.

[18]
Liang, L. (2006). h-index sequence and h-index matrix: Constructions and applications. Scientometrics, 69(1), 153-159.

[19]
Liu, Y., & Rousseau, R. (2008). Definitions of time series in citation analysis with special attention to the h-index. Journal of Informetrics, 2(3), 202-210.

[20]
Liu, Y., & Yang, Y. (2014). Empirical study of L-Sequence: The basic h-index sequence for cumulative publications with consideration of the yearly citation performance. Journal of Informetrics, 8(3), 478-485.

[21]
Mahbuba, D., & Rousseau, R. (2013). Year-based h-type indicators. Scientometrics, 96(3), 785-797.

[22]
Mahbuba, D., & Rousseau, R. (2016). New definitions and applications of year-based h-indices. COLLNET Journal of Scientometrics and Information Management, 10(2), 321-332.

[23]
Norris, M., & Oppenheim, C. (2010). The h-index: A broad review of a new bibliometric indicator. Journal of Documentation. 66(5), 756-773.

[24]
Schreiber, M., Malesios, C. C., & Psarakis, S. (2012). Exploratory factor analysis for the Hirsch index, 17 h-type variants, and some traditional bibliometric indicators. Journal of Informetrics, 6(3), 347-358.

[25]
Derek R. Smith (2015) “Platinum H”: Refining the H-Index to More Realistically Assess Career Trajectory and Scientific Publications. Archives of Environmental & Occupational Health, 70(2), 67-69. DOI: 10.1080/19338244.2015.1016833

[26]
Tol, R. (2009). The h-index and its alternatives: An application to the 100 most prolific economists. Scientometrics, 80(2), 317-324.

[27]
Wu, J., Lozano, S., & Helbing, D. (2011). Empirical study of the growth dynamics in real career h-index sequences. Journal of Informetrics, 5(4), 489-497.

Options
Outlines

/

〈 〉

京ICP备05002861号-43

Copyright © 2023 All rights reserved Journal of Data and Information Science

E-mail: jdis@mail.las.ac.cn　Add:No.33, Beisihuan Xilu, Haidian District, Beijing 100190, China

Support by Beijing Magtech Co.ltd　E-mail: support@magtech.com.cn