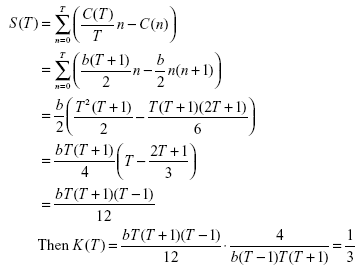1 Introduction
2 Naming of the concept
3 A new approach to determine articles with delayed recognition based on a cumulative citation curve
0 and T. Let cm > 0 be the maximum yearly number of received citations by this article, for which we assume that it happened in year tm, with 0 < tm ≤ T. The line connecting (0,c(0)) and the peak (tm,cm) = (tm,c(tm)), which is referred to as the recognition line, is denoted as y(t), and has equation:
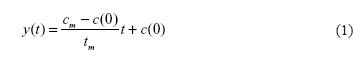
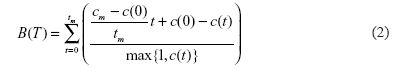
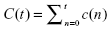 . Using a variation on the Du and Wu approach based on the cumulative citation curve we will propose a description of delayed recognition as a fuzzy phenomenon.
. Using a variation on the Du and Wu approach based on the cumulative citation curve we will propose a description of delayed recognition as a fuzzy phenomenon.4 Delayed recognition as a fuzzy phenomenon
here all choices are valid, i.e., have some scientific value, but the choice must be stated clearly.
B = 0. B is non-positive for papers whose citation trajectory is a concave function of time and positive for papers with a convex citation curve. Du and Wu (2017, 2018) proposed a similar measure, but based on the cumulative citation curve.
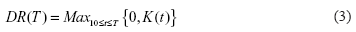

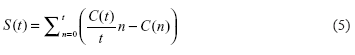
This happens if the publication receives its first citation in the year t. Yet, we are not interested in that year, but just use this value as a reference. For this case,
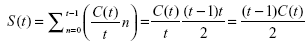 . Finally K(t) is defined as the ratio of the observed S(t) value over the largest possible one:
. Finally K(t) is defined as the ratio of the observed S(t) value over the largest possible one: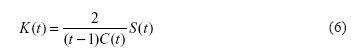
5 Examples
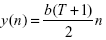 . Consequently, DR(T) = 1/3 (The calculation is included in the appendix). This result is different from the one obtained by using Ke et al.’s B. Their B-value is zero, although citations grow with time, indicating a delay in recognition. We further remark that this value for linear growth can be used as a kind of benchmark when comparing to other citation curves. Recall that linear growth in citation corresponds to quadratic growth in cumulative citations as illustrated in
. Consequently, DR(T) = 1/3 (The calculation is included in the appendix). This result is different from the one obtained by using Ke et al.’s B. Their B-value is zero, although citations grow with time, indicating a delay in recognition. We further remark that this value for linear growth can be used as a kind of benchmark when comparing to other citation curves. Recall that linear growth in citation corresponds to quadratic growth in cumulative citations as illustrated in Figure 1. Quadratic cumulative growth corresponding to linear growth. |
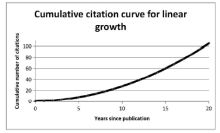
Figure 2. Cumulative citation curve of Romans (1986) and two recognition lines. |
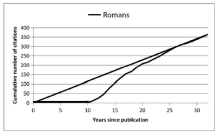
Figure 3. Cumulative citation curve of Leakey et al. (1964) and two recognition lines. |
Table 1 K-values for Leakey et al. (1964). |
| Year t | K(t) | Year t | K(t) | Year t | K(t) | Year t | K(t) |
|---|---|---|---|---|---|---|---|
| 1974 | 0.014 | 1985 | -0.019 | 1996 | -0.032 | 2007 | -0.007 |
| 1975 | 0.020 | 1986 | -0.055 | 1997 | -0.032 | 2008 | 0.027 |
| 1976 | 0.005 | 1987 | -0.053 | 1998 | -0.061 | 2009 | 0.061 |
| 1977 | -0.006 | 1988 | -0.011 | 1999 | -0.059 | 2010 | 0.060 |
| 1978 | -0.013 | 1989 | 0.013 | 2000 | -0.057 | 2011 | 0.085 |
| 1979 | -0.035 | 1990 | 0.016 | 2001 | -0.055 | 2012 | 0.102 |
| 1980 | -0.036 | 1991 | -0.015 | 2002 | -0.074 | 2013 | 0.145 |
| 1981 | -0.023 | 1992 | -0.026 | 2003 | -0.084 | 2014 | 0.151 |
| 1982 | 0.023 | 1993 | 0.005 | 2004 | -0.041 | 2015 | 0.164 |
| 1983 | 0.003 | 1994 | -0.022 | 2005 | -0.017 | 2016 | 0.194 |
| 1984 | -0.004 | 1995 | -0.023 | 2006 | -0.006 | 2017 | 0.225 |
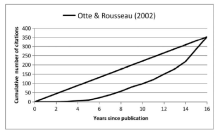
Figure 4. Cumulative citation curve of Otte and Rousseau (2002). |
Table 2 K-values for Otte and Rousseau (2002). |
| Year t | K(t) |
|---|---|
| 2011 | 0.515 |
| 2012 | 0.480 |
| 2013 | 0.476 |
| 2014 | 0.455 |
| 2015 | 0.464 |
| 2016 | 0.477 |
| 2017 | 0.523 |
6 Conclusion
Appendix: Calculation of DR(T) in the case of a linear increase in citations.